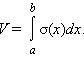- •I. Введение в анализ.
- •Предел функции в точке и на бесконечности. Геометрическая интерпретация. Теорема о единственности предела.
- •Бесконечно малые и бесконечно большие функции, их свойства
- •Теорема о связи функции с её пределом в точке
- •Алгебраические свойства пределов
- •Первый замечательный предел
- •Понятие предела последовательности. Теорема существования предела последовательности
- •Сравнение функций.
- •8. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции. Таблица эквивалентности
- •9. Понятие непрерывной функции в точке. Свойства непрерывных в точке функций
- •Свойства Локальные
- •Глобальные
- •10.Односторонние пределы функции в точке. Точки разрыва и их классификация.
- •Односторонний предел по Гейне
- •11.Основные теоремы о непрерывных на отрезке функциях
- •11. Дифференциальное исчисление функций одной перемен-
- •Правила дифференцирования функций
- •Производная сложной, обратной, параметрически заданной функции
- •Понятие дифференциала функции и его геометрический смысл. Применение дифференциала к приближенным вычислениям
- •Основные теоремы о дифференцируемых функциях (т.Ролля, Лагранжа, Коши)
- •Производные и дифференциалы высших порядков
- •Правило Лопиталя раскрытия неопределенностей. Раскрытие показательных неопределенностей
- •Формула Тейлора с остаточным членом в форме Лагранжа и Пеано
- •Разложение основных функций по формуле Тейлора
- •Монотонные функции. Признаки возрастания (убывания) функции на интервале
- •Понятие экстремума функции в точке. Необходимое и достаточное условия экс тремума функции в точке
- •Исследование функций на экстремум с помощью высших производных
- •Наибольшее и наименьшее значения функции на отрезке
- •Выпуклость и вогнутость графика функции, точка перегиба. Необходимое и достаточное условия точки перегиба графика функции
- •Понятие асимптоты графика функции. Нахождение вертикальных и наклонных асимптот
- •Полное исследование функции и построение графика функции
- •III. Неопределенный интеграл.
- •Понятие первообразной и ее свойства. Теорема о множестве первообразных
- •30.Таблица неопределенных интегралов основных функций
- •Интегрирование по частям и заменой переменной в неопределенном интеграле
- •Интегрирование функций с квадратным трехчленом в знаменателе
- •Интегрирование рациональных дробей методом разложения на простые дроби
- •Рекуррентные формулы. Вычисление интеграла
- •Интегрирование иррациональных функций
- •Интегрирование тригонометрических функций. Универсальная подстановка. Некоторые частные случаи
- •1.4 Интегрирование тригонометрических функций.
- •37.Интегралы, содержащие квадратичную иррациональность, и их вычисление с помощью тригонометрических подстановок
- •IV. Определенный интеграл.
- •Понятие определенного интеграла, его геометрический смысл, свойства
- •Определенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница
- •Интегрирование по частям и заменой переменной в определенном интеграле
- •Для неопределённого интеграла
- •Для определённого
- •Несобственные интегралы I и п рода. Определение, свойства, теоремы сравнения
- •Несобственные интегралы I рода
- •Геометрический смысл несобственного интеграла I рода
- •Примеры
- •Несобственные интегралы II рода
- •Геометрический смысл несобственных интегралов II рода
- •Геометрические приложения определенного интеграла:
- •43. Физические приложения определенного интеграла (работа переменной силы при прямолинейном перемещении материальной точки, давление жидкости на пластинку).
- •V. Функции многих переменных.
- •44. Функции многих переменных (фмп). Область определения, предел в точке, непрерывность
- •2. Предел функции.
- •Понятие частной производной фмп. Правила дифференцирования
- •Дифференцирование сложной функции многих переменных. Формула для производной неявно заданной функции одной переменной
- •Касательная плоскость и нормаль к поверхности
- •Частный и полный дифференциалы фмп. Применение дифференциала к приближенным вычислениям
- •Частные производные высших порядков. Теорема о равенстве смешанных производных
- •Дифференциалы высших порядков
- •Формула Тейлора для функции двух переменных
- •Различные формы остаточного члена
- •Экстремумы фмп. Необходимое и достаточное условия экстремума фмп в точке
- •Постановка задач на экстремум. Нахождение наибольшего и наименьшего значений функции в замкнутой области
-
Несобственные интегралы I и п рода. Определение, свойства, теоремы сравнения
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:
-
Предел a или b (или оба предела) являются бесконечными;
-
Функция f(x) имеет одну или несколько точек разрыва внутри интервала [a, b].
Несобственные интегралы I рода
Пусть f(x)
определена и непрерывна на множестве
от
![]() и
и
 .
Тогда:
.
Тогда:
-
Если
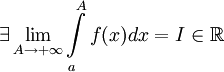 ,
то используется обозначение
,
то используется обозначение
 и
интеграл называется несобственным
интегралом Римана первого рода.
В этом случае
и
интеграл называется несобственным
интегралом Римана первого рода.
В этом случае
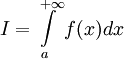 называется
сходящимся.
называется
сходящимся. -
Если не существует конечного
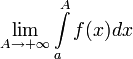 (
( или
или
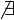 ),
то интеграл
),
то интеграл
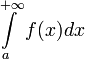 называется
расходящимся к
называется
расходящимся к
 ,
или просто расходящимся.
,
или просто расходящимся.
Пусть f(x)
определена и непрерывна на множестве
от
![]() и
и
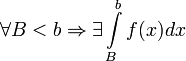 .
Тогда:
.
Тогда:
-
Если
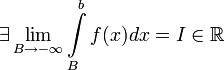 ,
то используется обозначение
,
то используется обозначение
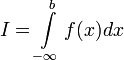 и
интеграл называется несобственным
интегралом Римана первого рода.
В этом случае
и
интеграл называется несобственным
интегралом Римана первого рода.
В этом случае
 называется
сходящимся.
называется
сходящимся. -
Если не существует конечного
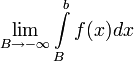 (
( или
или
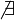 ),
то интеграл
),
то интеграл
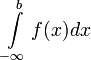 называется
расходящимся к
называется
расходящимся к
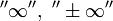 ,
или просто расходящимся.
,
или просто расходящимся.
Если функция f(x) определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:
 ,
где с — произвольное число.
,
где с — произвольное число.
Геометрический смысл несобственного интеграла I рода
Несобственный интеграл выражает площадь бесконечно длинной криволинейной трапеции.
Примеры
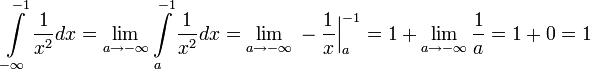
Несобственные интегралы II рода
Пусть f(x)
определена на (a,b],
терпит бесконечный разрыв в точке x=a и
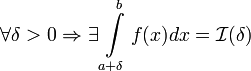 .
Тогда:
.
Тогда:
-
Если
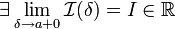 ,
то используется обозначение
,
то используется обозначение
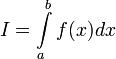 и
интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся.
и
интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся. -
Если
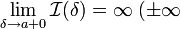 или
или
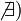 ,
то обозначение сохраняется, а
,
то обозначение сохраняется, а
 называется
расходящимся к
называется
расходящимся к
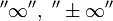 ,
или просто расходящимся.
,
или просто расходящимся.
Пусть f(x)
определена на [a,b)
, терпит бесконечный разрыв при x=b и
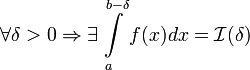 .
Тогда:
.
Тогда:
-
Если
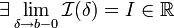 ,
то используется обозначение
,
то используется обозначение
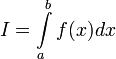 и
интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся.
и
интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся. -
Если
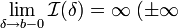 или
или
 ,
то обозначение сохраняется, а
,
то обозначение сохраняется, а
 называется
расходящимся к
называется
расходящимся к
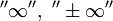 ,
или просто расходящимся.
,
или просто расходящимся.
Если функция f(x) терпит разрыв во внутренней точке c отрезка [a;b], то несобственный интеграл второго рода определяется формулой:
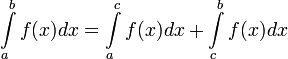
Геометрический смысл несобственных интегралов II рода
Несобственный интеграл выражает площадь бесконечно высокой криволинейной трапеции
Пример
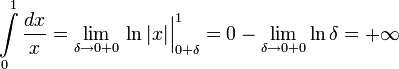
-
Геометрические приложения определенного интеграла:
а) вычисление площадей плоских фигур при различных способах задания уравнений ограничивающих линий;
Площадь
криволинейной трапеции, ограниченной
неотрицательной функцией f ( x ), осью
абсцисс и прямыми x = a , x =
b , определяется как
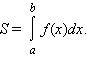
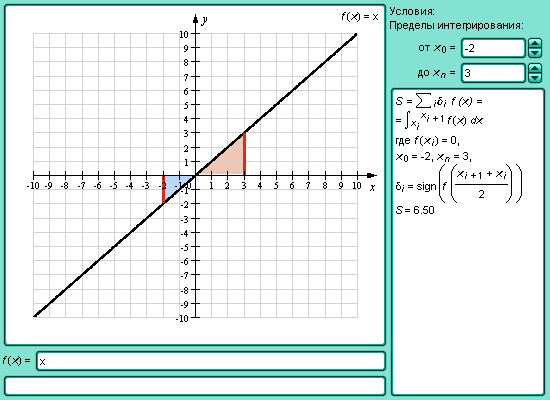
Модель 3.11. Площадь криволинейной трапеции.
Площадь
фигуры, ограниченной функцией f ( x
), пересекающей ось абсцисс, определяется
формулой
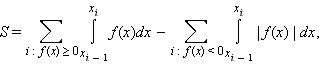 где
x i –
нули функции. Другими словами, чтобы
вычислить площадь этой фигуры, нужно
разбить отрезок [ a ; b ] нулями функции
f ( x ) на части, проинтегрировать
функцию f по каждому из получившихся
промежутков знакопостоянства, сложить
отдельно интегралы по отрезкам, на
которых функция f принимает разные
знаки, и вычесть из первого второе.
где
x i –
нули функции. Другими словами, чтобы
вычислить площадь этой фигуры, нужно
разбить отрезок [ a ; b ] нулями функции
f ( x ) на части, проинтегрировать
функцию f по каждому из получившихся
промежутков знакопостоянства, сложить
отдельно интегралы по отрезкам, на
которых функция f принимает разные
знаки, и вычесть из первого второе.
б) вычисление длин дуг линий при различных способах задания уравнений линий;
Пусть
задана кривая
![]() Тогда
длина ее участка, ограниченного значениями
t = α и t = β выражается формулой
Тогда
длина ее участка, ограниченного значениями
t = α и t = β выражается формулой

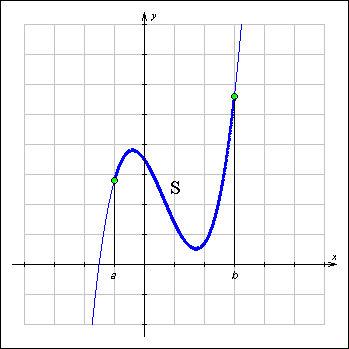 Рисунок
3.4.4.3. В частности, длина плоской кривой,
задаваемой на координатной плоскости
OXY уравнением y = f ( x ), a ≤
x ≤ b , выражается формулой
Рисунок
3.4.4.3. В частности, длина плоской кривой,
задаваемой на координатной плоскости
OXY уравнением y = f ( x ), a ≤
x ≤ b , выражается формулой

5. Площадь поверхности вращения.
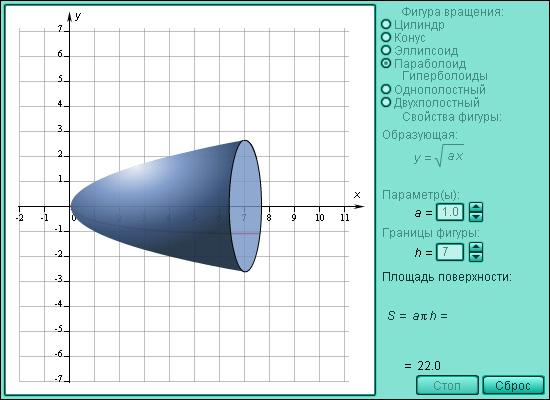
Модель 3.13. Площадь поверхности вращения.
Пусть
поверхность задается вращением
относительно оси OX графика функции y
= f ( x ), a ≤ x ≤ b ,
и функция f имеет непрерывную производную
на этом отрезке. Тогда площадь поверхности
вращения определяется формулой
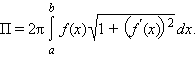
в) вычисление объемов и площади поверхности тел вращения.
3. Объем тела вращения.
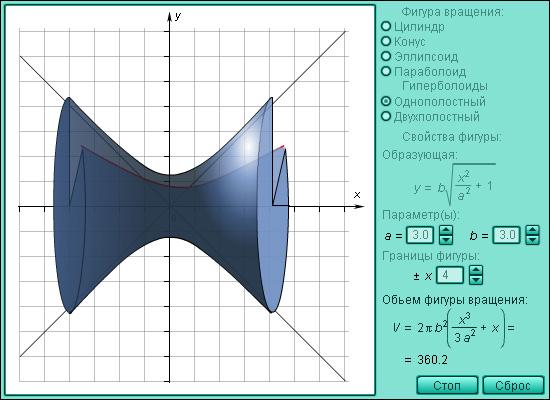
Модель 3.12. Объем тела вращения.
Пусть
тело образовано вращением вокруг оси
OX криволинейной трапеции, ограниченной
непрерывной на отрезке [ a ; b ] функцией
f ( x ). Его объем выражается формулой
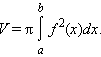
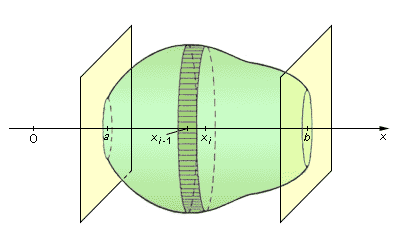 Рисунок
3.4.4.2.
Рисунок
3.4.4.2.
Пусть
тело заключено между плоскостями x =
a и x = b , а площадь его сечения
плоскостью, проходящей через точку x ,
– непрерывная на отрезке [ a ; b ]
функция σ ( x ). Тогда его объем равен