12. Понятие дифференциала функции и его геометрический смысл. Применение дифференциала к приближенным вычислениям

Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)):

dy=ƒ'(х)•∆х.                                             (24.1)

Дифференциал dу называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции у=х.

Так как у'=х'=1, то, согласно формуле (24.1), имеем dy=dx=∆x, т. е. дифференциал независимой переменной равен приращению этой переменной: dх=∆х.

Выясним геометрический смысл дифференциала.

Для этого проведем к графику функции у=ƒ(х) в точке М(х; у) касательную МТ и рассмотрим ординату этой касательной для точки х+∆х (см. рис. 138). На рисунке  АМ =∆х, |AM₁|=∆у. Из прямоугольного треугольника МАВ имеем:

Но, согласно геометрическому смыслу производной, tga=ƒ'(х). Поэтому АВ=ƒ'(х)•∆х.

Сравнивая полученный результат с формулой (24.1), получаем dy=АВ, т. е. дифференциал функции у=ƒ(х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение ∆х.

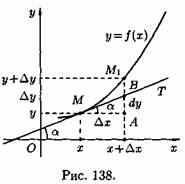
В этом и состоит геометрический смысл дифференциала.

Как уже известно, приращение ∆у функции у=ƒ(х) в точке х можно представить в виде ∆у=ƒ'(х)•∆х+α•∆х, где α→0 при ∆х→0, или ∆у=dy+α•∆х. Отбрасывая бесконечно малую α•∆х более высокого порядка, чем ∆х, получаем приближенное равенство

∆у≈dy,                                              (24.3)

причем это равенство тем точнее, чем меньше ∆х.

Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции.

Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула (24.3) широко применяется в вычислительной практике.

<< Пример 24.3

Найти приближенное значение приращения функции у=х³-2х+1 при х=2 и ∆х=0,001.

Решение: Применяем формулу (24.3): ∆у≈dy=(х³-2х+1)'•∆х=(3х²-2)•∆х.

Итак, ∆у 0,01.

Посмотрим, какую погрешность допустили, вычислив дифференциал функции вместо ее приращения. Для этого найдем ∆у:

∆у=((х+∆х)³-2(х+∆х)+1)-(х³-2х+1)=х³+3х²•∆х+3х•(∆х)²+(∆х)³-2х-2•∆х+1-х³+2х-1=∆х(3х²+3х•∆х+(∆х)²-2);

Абсолютная погрешность приближения равна

|∆у-dy|=|0,010006-0,011=0,000006.

Подставляя в равенство (24.3) значения ∆у и dy, получим

ƒ(х+∆х)-ƒ(х)≈ƒ'(х)∆х

или

ƒ(х+∆х)≈ƒ(х)+ƒ'(х)•∆х.                            (24.4)

Формула (24.4) используется для вычислений приближенных значений функций.

17. Основные теоремы о дифференцируемых функциях (т.Ролля, Лагранжа, Коши)

Теорема 5.2 (Ролля)   Пусть функция дифференцируема на интервале , непрерывна в точках и и принимает в этих точках значение 0: . Тогда найдётся хотя бы одна точка , в которой .

        Замечание 5.2   Это утверждение можно переформулировать так: между двумя корнями и дифференцируемой функции обязательно найдётся корень её производной (то есть точка , такая что ). Условие означает, что касательная, проведённая к графику при , расположена горизонтально.

Заметим также, что теорема Ролля не утверждает, что корень  -- единственный корень производной на интервале ; на этом интервале может находиться несколько корней производной.     

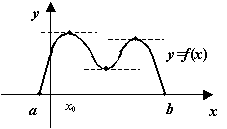
Рис.5.4.Между двумя корнями дифференцируемой функции лежит хотя бы один корень её производной

        Доказательство теоремы Ролля.     Так как при наших предположениях функция непрерывна на отрезке , то она принимает своё максимальное значение и минимальное значение в некоторых точках и этого отрезка.

Рассмотрим два случая. Если , то наибольшее и наименьшее значения функции совпадают, и, следовательно, функция постоянна на отрезке : . Значит, при всех , и в качестве в этом случае можно взять любую точку интервала .

Если же , то либо , либо отлично от 0 и, следовательно, либо точка , либо точка не совпадает с концами отрезка и , то есть лежит внутри интервала . Пусть, для определённости,  -- внутренняя точка интервала. Тогда, по теореме Ферма, , поскольку по предположению доказываемой теоремы, имеет производную во всех точках интервала и, следовательно, в точке . Итак, в этом случае точку можно взять в качестве искомой точки : тогда .     

        Теорема 5.3 (Лагранжа)   Пусть функция дифференцируема на интервале и непрерывна в точках и . Тогда найдётся такая точка , что

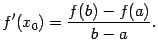(5.1

        Замечание 5.3   Формулу (5.1) можно записать в виде

5.2)

Если считать, что аргументу придано приращение , то функция получает приращение . (При этом мы не считаем, что и стремятся к 0, то есть это конечные, а не бесконечно малые, приращения.) При этих обозначениях формулу (5.2) мы можем записать в виде

в котором участвуют конечные приращения аргумента и функции. Поэтому формулу (5.2) называют формулой конечных приращений.     

        Доказательство теоремы Лагранжа.     Дадим сначала геометрическую иллюстрацию теоремы. Соединим конечные точки графика на отрезке хордой. Конечные приращения и  -- это величины катетов треугольника, гипотенузой которого служит проведённая хорда.

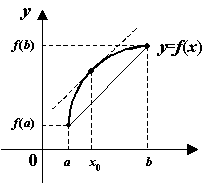
Рис.5.5.Касательная в некоторой точке параллельна хорде

Отношение конечных приращений и  -- это тангенс угла наклона хорды. Теорема утверждает, что к графику дифференцируемой функции можно провести в некоторой точке касательную, которая будет параллельна хорде, то есть угол наклона касательной ( ) будет равен углу наклона хорды ( 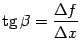). Но наличие такой касательной геометрически очевидно.

Заметим, что проведённая хорда, соединяющая точки и  -- это график линейной функции . Поскольку угловой коэффициент этой линейной функции равен, очевидн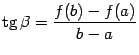о, , то

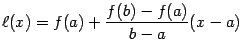
(мы учли то, что график линейной функции проходит через точку ).

Сведём доказательство к применению теоремы Ролля. Для этого введём вспомогательную функцию , то есть

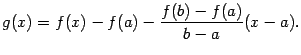
Заметим, что и (по построению функции ). Так как линейная функция дифференцируема при всех , то функция удовлетворяет, тем самым, всем свойствам, перечисленным в условии теоремы Ролля. Поэтому найдётся такая точка , что .

Заметим теперь, что

Значит, равенство можно переписать в виде

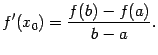
Таким образом, мы доказали формулу (5.1).      Из теоремы Лагранжа вытекает утверждение, обратное к тому, что производная постоянной есть 0, а именно: Теорема 5.4 (Коши)   Пусть функции и дифференцируемы на интервале и непрерывны при и , причём при всех . Тогда в интервале найдётся такая точка , что

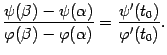
        Доказательство.     Докажем сначала, что , то есть что дробь в левой части формулы имеет смысл. Действительно, для этой разности можно записать формулу конечных приращений:

при некотором . Но в правой части этой формулы оба множителя отличны от нуля.

Для доказательства теоремы применим тот же приём, что при доказательстве теоремы Лагранжа: введём вспомогательную функцию

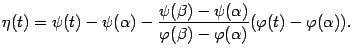Функция , очевидно, является дифференцируемой при всех и непрерывной в точках и , поскольку этими свойствами обладают функции и . Кроме того, очевидно, что при получается . Покажем, что и :

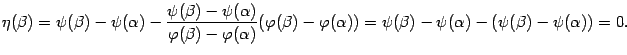Значит, функция удовлетворяет на отрезке условиям теоремы Ролля. Поэтому существует такая точка , что . Вычислим теперь производную функции :

Получаем, что

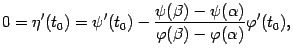
откуда получаем утверждение теоремы:

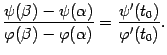
Замечание 5.4   Можно считать функции и координатами движущейся на плоскости точки, которая описывает линию , соединяющую начальную точку с конечной точкой . (Тогда уравнения и параметрически задают некоторую зависимость , графиком которой служит линия .)

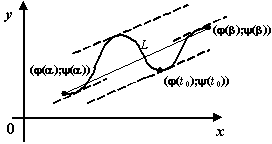
Рис.5.6.Хорда параллельна некоторой касательной к кривой

Отношение , как нетрудно видеть из чертежа, задаёт тогда угловой коэффициент хорды, соединяющей точки и . В то же время, по формуле производной функции, заданной параметрически, имеем: 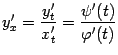. Значит, дробь  -- это угловой коэффициент касательной к линии в некоторой точке . Тем самым утверждение теоремы означает, с геометрической точки зрения, что на линии найдётся точка, такая что проведённая в этой точке касательная параллельна хорде, соединяющей крайние точки линии. Но это -- то же самое утверждение, которое составляло геометрический смысл теоремы Лагранжа. Только в теореме Лагранжа линия была задана явной зависимостью , а в теореме Коши -- зависимостью, заданной в параметрической форме.