10.Односторонние пределы функции в точке. Точки разрыва и их классификация.

Односторонний предел в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторонним пределом (или пределом слева) и правосторонним пределом (пределом справа). Пусть на некотором числовом множестве задана числовая функция и число — предельная точка области определения . Существуют различные определения для односторонних пределов функции в точке , но все они эквивалентны.

Односторонний предел по Гейне

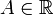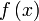• Число называется правосторонним пределом (правым пределом, пределом справа) функции в точке 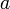, если для всякой последовательности 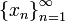, состоящей из точек, больших числа 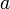, которая сама сходится к числу 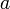, соответствующая последовательность значений функции сходится к числу .

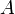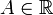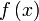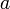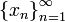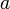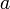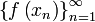• Число называется левосторонним пределом (левым пределом, пределом слева) функции в точке , если для всякой последовательности , состоящей из точек, меньших числа , которая сама сходится к числу , соответствующая последовательность значений функции сходится к числу .

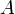11.Основные теоремы о непрерывных на отрезке функциях

Теорема 4.1. Сумма конечного числа непрерывных функций, определенных на некотором множестве Х, есть функция непрерывная.

Теорема 4.2. Произведение конечного числа непрерывных функций есть функция непрерывная.

С л е д с т в и е. Целый полином Р(х)=а₀+а₁х+... +а_nхⁿ есть функция непрерывная.

Теорема 4.3. Частное от деления двух непрерывных функций есть функция непрерывная во всех точках, в которых делитель отличен от нуля.

Теорема 4.4. Непрерывная функция от непрерывной функции есть функция непрерывная.

Теорема 4.5. Если y = f(x) непрерывна и строго монотонна на промежутке <а,b> , то существует обратная функция х = j(y), определенная на промежутке < f(a), f(b) >, причем последняя также монотонна и непрерывна в том же смысле.

В качестве упражнения теоремы 4.1. - 4.5. - доказать самостоятельно.

Пример. Рассмотреть обратные функции к данным:

а) ; б) .

Рассмотрим теперь непрерывность функции на множествах.

Определение 4.5. Пусть f определена на множестве Е Ì Rn . Функция f называется непрерывной в точке х(0) Î Е, если " e>0 $ d=d(e) : " х Î Х , удовлетворяющих условию r(х, х(0)) < d выполняется неравенство çf(x)- f(x(0)) ç < e .

Примем без доказательства ряд простых, но важных теорем.

Теорема 4.6. (Кантора) Функция, непрерывная на ограниченном замкнутом множестве, является равномерно непрерывной.

Т

Определение 4.6. Функция у = f(х), определенная на множестве Е Ì Rn называется равномерно непрерывной на Е, если " e > 0 $ d = d(e)>0 : " x/, x// Î E удовлетворяющих условию r(x/,x//)<d будет выполнено неравенство çf(x/) - f(x//) ç< e .

еорема 4.7. (Вейерштрасса) Всякая непрерывная на отрезке функция имеет на этом отрезке как наибольшее, так и наименьшее значение.

Теорема 4.8. (Коши) Если f - непрерывна на [a, b] и f(b) = A, f(b) = B, то

" A < C < B $ x Î [a, b] : f(x) = C.

С л е д с т в и е. Если f - непрерывна на [a, b], а на концах отрезка принимает значения переменных знаков (является знакопеременной), то $ точка

х₀ Î [a,b] : f(x₀) = 0.