31. Интегрирование по частям и заменой переменной в неопределенном интеграле

ПРИМЕР 1.  Простейшие методы интегрирования

Интегрирование заменой переменной - Если — непрерывно дифференцируемая функция, то, полагая  , получим формулу интегрирования заменой переменной   . Если замена переменной выбрана правильно, то интеграл в правой части должен легко вычисляться. Для некоторых классов функций существуют стандартные замены, сводящие интеграл к табличному.

ПРИМЕР 2.  Замена переменной в неопределенном интеграле

Интегрирование по частям - Пусть  - непрерывно дифференцируемые функции. Тогда справедлива формула интегрирования по частям . Название “по частям” связано с тем, что для записи интеграла в правой части нужно проинтегрировать “часть”    подынтегрального выражения в левой части. Метод интегрирования по частям используется для интегралов вида   ,  ,  ,  и некоторых других.

31. Интегрирование функций с квадратным трехчленом в знаменателе

Рассмотрим интеграл , содержащий квадратный трехчлен в знаменателе подынтегрального выражения. Такой интеграл берут также методом подстановки, предварительно выделив в знаменателе полный квадрат. Покажем это на примерах.

Пример 12. Вычислить .

Решение. Преобразуем , выделяя полный квадрат по формуле . Тогда ;

 

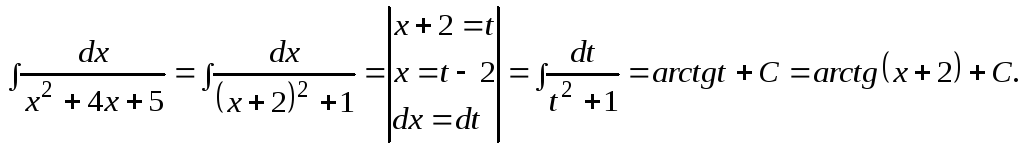
Пример 13. Вычислить .

Решение. Преобразуем . Тогда =.

31. Интегрирование рациональных дробей методом разложения на простые дроби

Если P(z) и Q(z) – многочлены в комплексной области, то - рациональная дробь. Она называется правильной, если степень P(z) меньше степени Q(z), и неправильной, если степень Р не меньше степени Q.

Любую неправильную дробь можно представить в виде: ,

где

P(z) = Q(z) S(z) + R(z),

a R(z) – многочлен, степень которого меньше степени Q(z).

Таким образом, интегрирование рациональных дробей сводится к интегрированию многочленов, то есть степенных функций, и правильных дробей, так как является правильной дробью.

Определение 5. Простейшими (или элементарными) дробями называются дроби следующих видов:

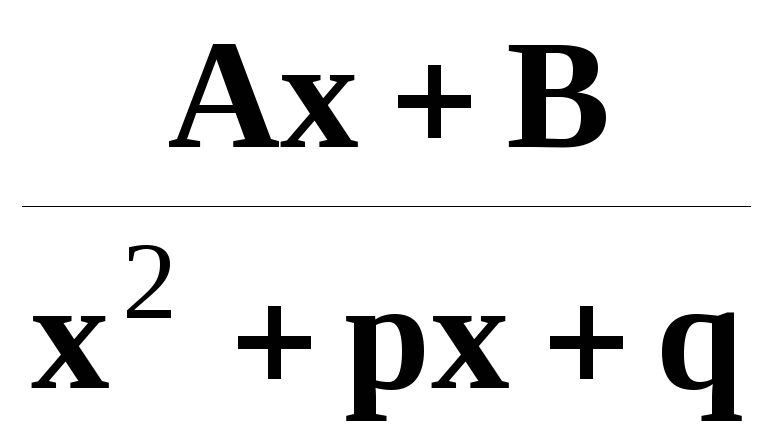1) , 2) , 3) , 4) .

Выясним, каким образом они интегрируются.

1)

2)

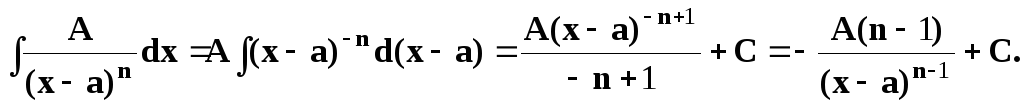
3) .

Теорема 5. Всякую правильную дробь можно представить в виде суммы простейших дробей (без доказательства).

Следствие 1. Если - правильная рациональная дробь, и если среди корней многочлена будут только простые действительные корни, то в разложении дроби на сумму простейших дробей будет присутствовать лишь простейшие дроби 1-го типа:

31. Рекуррентные формулы. Вычисление интеграла

Рекуррентная формула — формула вида , , выражающая каждый член последовательности a_n () через предыдущих членов.

Общая проблематика рекуррентных вычислений является предметом теории рекурсивных функций.

• Вычисление интеграла вида :

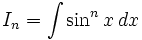35. Интегрирование иррациональных функций

Для интегрирования иррациональной функции, содержащей используется подстановка . Чтобы проинтегрировать иррациональную функцию, содержащую несколько рациональных степеней x, применяется подстановка в форме , где n полагается равным наименьшему общему кратному знаменателей всех дробных степеней, входящих в данную функцию. Рациональная функция x под знаком корня n-ой степени, т.е. выражение вида , интегрируется с помощью подстановки .

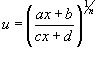   Пример 1

Найти интеграл .

Решение.

Сделаем подстановку:

     

Вычислим интеграл