2. Предел функции.

Определение. Будем говорить, что последовательность точек сходится при к точке , если при .

В этом случае точку называют пределом указанной последовательности и пишут: при .

Легко показать, что тогда и только тогда, когда одновременно , (т.е. сходимость последовательности точек пространства эквивалентна покоординатной сходимости).

Пусть и – предельная точка множества .

Определение. Число называют пределом функции при , если для такое, что , как только . В этом случае пишут

или при .

При кажущейся полной аналогии понятий предела функций одной и двух переменных существует глубокое различие между ними. В случае функции одной переменной для существования предела в точке необходимо и достаточно равенство лишь двух чисел – пределов по двум направлениям: справа и слева от предельной точки . Для функции двух переменных стремление к предельной точке на плоскости может происходить по бесконечному числу направлений (и необязательно по прямой), и потому требование существования предела у функции двух (или нескольких) переменных «жестче» по сравнению с функцией одной переменной.

45. Понятие частной производной фмп. Правила дифференцирования

В математическом анализе, частная производная — одно из обобщений понятия производной на случай функции нескольких переменных.

В явном виде частная производная функции f определяется следующим образом:

График функции z = x² + xy + y². Частная производная в точке (1, 1, 3) при постоянном y соответствует углу наклона касательной прямой, параллельной плоскости xz.

Сечения графика, изображенного выше, плоскостью y= 1

Следует обратить внимание, что обозначение следует понимать как цельный символ, в отличие от обычной производной функции одной переменной , которую можно представить, как отношение дифференциалов функции и аргумента. Однако, и частную производную можно представить как отношение дифференциалов, но в этом случае необходимо обязательно указывать, по какой переменной осуществляется приращение функции: , где d_xf — частный дифференциал функции f по переменной x. Часто непонимание факта цельности символа является причиной ошибок и недоразумений, как, например, сокращение в выражении . (подробнее см. Фихтенгольц, «Курс дифференциального и интегрального исчисления»).

Геометрически, частная производная является производной по направлению одной из координатных осей. Частная производная функции f в точке по координате x_k равна производной по направлению , где единица стоит на k-ом месте.

правил дифференцирования.

1. Сумма и произведение дифференцируемых в точке функций,  есть функция и справедливы равенства:

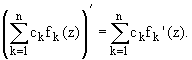
2. Частное дифференцируемых в точке функций, при условии, что знаменатель в точке не равен нулю, есть дифференцируемая в этой точке функция, :

45. Дифференцирование сложной функции многих переменных. Формула для произ­водной неявно заданной функции одной переменной

Сложная функция f( (z)) дифференцируема в точке z₀, если в этой точке дифференцируема функция  (z), а функция f(u) дифференцируема в точке u₀, где u₀ =  (z₀) и u =  (z). При этом в точке z₀ имеет место формула:

Для элементарных функций комплексного переменного справедливы формулы дифференцирования, установленные для действительных значений аргумента. Например, рассмотрим функцию  f(z) = z³. По определению производной для любой точки z, принадлежащей комплексной области, записываем:

Предел существует для любой точки z, принадлежащей комплексной области и (z³)' =3z². Аналогично можно получить: (zⁿ)' = nz^n-1 (n - действительное число).

 

ПРИМЕР 1. Вычисление значения производной функции коплексного переменного в точке.

 

Если f(z) = f(x+iy) = u(x, y) + iv(x, y), т.е. u(x, y) = Re f(z) и v(x, y) = Im f(z), то справедливы следующие утверждения:

1. Если функция f(z) дифференцируема в точке, то в этой точке существуют частные производные ее действительной и мнимой частей u(x, y) = Re f(z),   v(x, y) = Im f(z) и выполняется условие Коши-Римана:

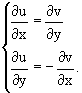
2. Если u(x, y)  и v(x, y) дифференцируемы в точке (x₀, y₀) (имеют непрерывные частные производные в этой точке) и выполняется условие Коши-Римана, то функция   f(z) = f(x+iy) = u(x, y) + iv(x, y)  дифференцируема в точке z₀ = x₀+ iy₀.

3. Производная дифференцируемой функции может быть записана по одной из формул:

Неявная функция одной переменной. Пусть в некоторой области  плоскости задана функция , и пусть линия уровня этой функции , определяемая уравнением  , является графиком некоторой функции   , определяемой уравнением   . В этом случае говорят, что функция    задана неявно уравнением  . Для существования неявной функции требуется выполнение следующих условий: функция   и ее частная производная по   непрерывны в    , . Тогда в некоторой окрестности точки  существует единственная непрерывная функция     , задаваемая уравнением   , так, что в этой окрестности   .

 

ПРИМЕР 1.  Построение графиков неявных функций одной переменной.

 

Неявная функция многих переменных. Аналогично рассматривают функции многих переменных, заданные неявно. Например, при выполнении соответствующих условий, уравнение    задает неявно функцию  . Это же уравнение может задавать неявно функцию или     .