9.5. Явления переноса. Длина свободного пробега молекул

В предыдущих разделах мы рассматривали свойства тел, находящихся в тепловом равновесии. Данный раздел посвящен процессам, с помощью которых происходит установление состояния равновесия. Такие процессы называют кинетическими. Эти процессы являются необратимыми, к ним относятся явления диффузии, вязкости и теплопроводности.

Большое значение при анализе этих процессов имеет свободный пробег молекул. Среднее расстояние, которое проходит молекула между двумя последовательными соударениями, называют средней длиной свободного пробега молекул или просто длиной свободного пробега, которую обозначают сим волом . При соударении молекулы сближаются. Минимальное расстояние, на которое сближаются центры двух молекул при соударении, называется эффективным диаметром молекулы d. За секунду молекула проходит в среднем путь, равный средней скорости молекул v_ср. Если за секунду молекула претерпевает  соударений, то длина свободного пробега

 = v_ср /. (9.24)

Д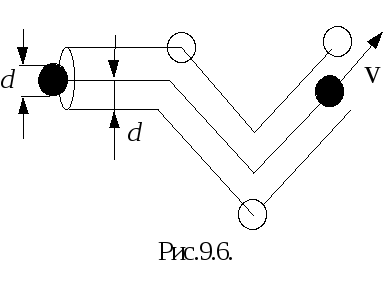ля расчета числа соударений предположим вначале, что все молекулы покоятся, а одна движется и соударяется с ними (рис.9.6) . Молекула будет сталкиваться с другими молекулами, если их центры будут лежать внутри ломаного цилиндра, имеющего диаметр, равный d. За секунду молекула проходит путь, равный v_ср., и объем ломаного цилиндра, пройденного молекулой, равен d²v_ср. Умножив этот объем на число молекул в единице объема n, получим среднее число соударений молекулы за секунду: v_срn . Так как остальные молекулы также движутся, то, как показывают расчеты, соударения происходят в раз чаще. Следовательно, истинное среднее число соударений молекулы за секунду

 = v_срn. (9.25)

Подставив это значение  в (9.24), получим для средней длины свободного пробега молекул следующую формулу:

 = 1/(n). (9.26)

При постоянной температуре n пропорционально давлению. Следовательно, средняя длина свободного пробега молекул обратно пропорциональна давлению. При нормальных условиях расчет по формуле (10.26) для молекул воздуха дает  = 210^-7 м. Длина свободного пробега получается в 1000 раз больше эффективного диаметра d = 210^-10 м. С уменьшением давления длина свободного пробега растет и может стать сравнимой с размерами сосуда и больше их. Такое состояние газа называют вакуумом.

9.6. Явление диффузии

Диффузией называют процесс взаимного проникновения молекул соприкасающихся веществ, обусловленный тепловым движением. Этот процесс наблюдается в газах, жидкостях и твердых телах. Например, распространение запаха в неподвижном воздухе можно объяснить явлением диффузии.

Для описания процесса диффузии необходимо ввести понятие парциальной плотности вещества _i, которая равна массе i-того диффундирующего вещества, находящейся в единице объема смеси. Пусть диффузия происходит в направлении оси z и является стационарной, т.е. величина _i в точках среды остается постоянной с течением времени. Закон диффузии экспериментально установил ученый Фик: масса вещества M, проходящая за время t через площадку S, перпендикулярную к направлению диффузии, равна

M = -DSt, (9.27)

где d_i - изменение парциальной плотности вещества вдоль расстояния dz; знак минус показывает, что диффузия направлена в сторону убывания _i; D - коэффициент диффузии. Величину d_i /dz называют градиентом парциальной плотности (понятие градиента подробно рассмотрено в подразд.3.5). Этот градиент показывает скорость уменьшения парциальной плотности вещества вдоль направления диффузии. Если численно положить d_i /dz = -1 , S = 1 , t = 1 , то получим из (9.27) M = D . Отсюда следует физический смысл D : коэффициент диффузии численно равен массе вещества, перенесенной за единицу времени через единичную площадку, расположенную перпендикулярно направлению диффузии, если модуль градиента парциальной плотности равен единице. Размерность коэффициента диффузии [ D] = м²с^-1.

Р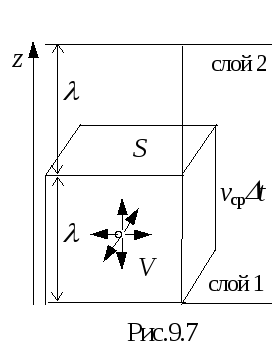ассмотрим вывод этого закона для газов, исходя из молекулярно-кинетических представлений. Для упрощения расчетов будем считать, что молекулы обеих компонент смеси газов имеют практически одинаковые массы и размеры. Результат оценочного расчета не изменится, если хаотичное движение молекул заменить их упорядоченным движением вдоль осей x , y и z . Тогда через площадку S в направлении оси z за время t пролетит лишь 1/6 часть тех молекул, которые находятся в объеме V = Sv_срt , где v_ср - средняя скорость молекул (рис.9.7). Число таких молекул равно n₁Sv_срt/6 , где n₁ - число молекул диффундирующего газа в единице объема для слоя 1. Аналогично сверху вниз через площадку S из слоя 2 пролетит число молекул, равное n₂Sv_срt/6 , где n₂ - число молекул диффундирующего газа в единице объема для слоя 2. Разность этих чисел даст число молекул, пролетевших через площадку S в направлении оси z: N =(n₁ - n₂)Sv_срt/6. Эти пролетевшие молекулы перенесут через площадку S массу вещества M = mN или M = m(n₁ - n₂)Sv_срt/6 , где m - масса молекулы. Подставляя парциальные плотности вещества _i1 = mn₁ и _i2 = mn₂ , получим

M = (_i1 - _i2)Sv_срt/6. (9.28)

Свободно пролетать площадку S могут лишь те молекулы, которые находятся от нее на расстоянии, не превышающем среднюю длину свободного пробега молекул . Следовательно, слои 1 и 2 должны находиться на расстоянии друг от друга, равном 2 , и в согласии с определением градиента должно выполняться соотношение (_i2 - _i1)/ 2 = d_i /dz. Учитывая это равенство, преобразуем выражение (9.28) к виду

M = - (1/3) v_ср(d_i /dz)St. (9.29)

Мы получили закон диффузии, используя молекулярно-кинетические представления. Сравнивая равенства (10.29) и (10.27), получим теоретическое выражение для коэффициента диффузии

D = (1/3) v_ср. (9.30)

Так как   1/p , то D уменьшается при увеличении давления. Зависимость коэффициента диффузии от v_ср., а следовательно, и от массы молекул, позволяет использовать явление диффузии для разделения изотопов при многократном прохождении газа через пористые перегородки.

Поток паров от кипящей ртути, направленный вдоль специальной трубы, позволяет на ее концах создать разность давлений откачиваемого газа от 1 мм.рт.ст до 10^-7 мм рт.ст., достаточную для получения высокого вакуума. Для откачиваемого газа только одна из 10²⁰ молекул способна пробиться через поток паров ртути за счет диффузии. Устройство, основанное на этом принципе получения вакуума, называют диффузионным насосом. Предварительную откачку газа до 1 мм рт.ст. производят другими насосами.