§4. Механика твердого тела.

4.1. Поступательное движение твердого тела.

ОПРЕДЕЛЕНИЕ: Абсолютно твердым телом будем называть такое тело, деформациями которого в условиях рассматриваемой задачи можно пренебречь.

или

Абсолютно твердым телом называется такое тело, у которого расстояние между его частями сохраняется неизменным за все время движения.

Всякое движение твердого тела можно разложить на два основных вида движения – поступательное и вращательное.

Рассмотрим первый из них.

ОПРЕДЕЛЕНИЕ: Поступательное движение – это такое движение, при котором любая прямая, связанная с движущимся телом, остается параллельной самой себе (рис. 4.1).

П

Рис. 4.1

ри поступательном движении все точки тела получают за один и тот же промежуток времени равные по величине и направлению перемещения, вследствие чего скорости и ускорения всех точек в каждый момент времени оказываются одинаковыми. Наиболее простым видом поступательного движения является прямолинейное движение. В этом случае траектории всех точек тела – параллельные прямые.

Рассмотрим движение твердого тела, представив его как систему материальных точек с элементарной массой m_i. Каждая из этих элементарных масс может находиться под воздействием как внутренних сил , обусловленных ее взаимодействием с другими элементарными массами рассматриваемого тела, так и внешних сил .

Напишем для каждой элементарной массы II закон Ньютона:

,

где и – результирующие всех внутренних и внешних сил, приложенных к данной элементарной массе.

Складывая эти уравнения для всех элементарных масс, получим

.

Сумма всех внутренних сил , тогда имеем . Здесь – результирующая всех внешних сил, действующих на тело.

Рассмотрим теперь сумму, стоящую в левой части уравнения.

ОПРЕДЕЛЕНИЕ: Назовем центром инерции (центром масс) системы точку, положение которой в пространстве задается радиус-вектором , определяемым следующим образом: 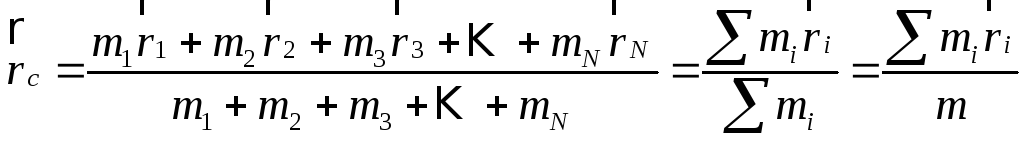, где m_i – масса i-го тела, – радиус вектор, определяющий положение этого тела в пространстве, m – масса системы.

Продифференцируем дважды радиус-вектор центра инерции по времени и учитывая, что и , сумму в левой части можно записать в виде .

Следовательно,

– закон движения центра инерции твердого тела.

ОПРЕДЕЛЕНИЕ: Центр инерции твердого тела движется так, как двигалась бы материальная точка с массой равной массе тела, под действием всех приложенных к телу сил.

В случае поступательного движения это уравнение будет определять ускорение не только центра инерции, но любой другой точки тела.

4.2. Вращательное движение твердого тела.

ОПРЕДЕЛЕНИЕ: Вращательным движением твердого тела будем называть такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и ой же прямой, называемой осью вращения.

Для изучения динамики вращательного к известным кинематическим величинам добавляются ещё две величины: момент силы (M) и момент инерции (J).

1. Из опыта известно: ускорение вращательного движения зависит не только от величины силы, действующей на тело, но и от расстояния от оси вращения до линии, вдоль которой действует сила. Для характеристики этого обстоятельства вводится физическая величина называемая моментом силы.

Рассмотрим простейший случай.

О

Рис. 4.2

ПРЕДЕЛЕНИЕ: Моментом силы относительно некоторой точки “O” называется векторная величина , определяемая выражением , где – радиус-вектор, проведенный из точки “O” в точку приложения силы.

Из определения следует, что является аксиальным вектором. Его направление выбрано так, что вращение вектора вокруг точки “O” в направлении силы и вектор образуют правовинтовую систему. Модуль момента силы равен , где  – угол между направлениями векторов и , а l = r·sin – длина перпендикуляра, опущенного из точки “O” на прямую, вдоль которой действует сила (называется плечом силы относительно точки “O”) (рис. 4.2).

2. Опытные данные свидетельствуют, что на величину углового ускорения оказывает влияние не только масса вращающегося тела, но и распределение массы относительно оси вращения. Величина, учитывающая это обстоятельство, носит название момента инерции относительно оси вращения.

ОПРЕДЕЛЕНИЕ: Строго говоря, моментом инерции тела относительно некоторой оси вращения называется величина J, равная сумме произведений элементарных масс на квадраты их расстояний от данной оси .

Суммирование проводится по всем элементарным массам, на которые было разбито тело. Следует иметь ввиду, что эта величина (J) существует безотносительно к вращению (хотя понятие момента инерции было введено при рассмотрении вращения твердого тела).

Каждое тело независимо от того покоится оно или вращается обладает определенным моментом инерции относительно любой оси, подобно тому как тело обладает массой независимо от того движется оно или покоится.

Учитывая, что , момент инерции можно представить в виде: . Это соотношение приближенно и оно будет тем точнее, чем меньше элементарные объемы и соответствующие им элементы массы. Следовательно, задача нахождения моментов инерции сводится к интегрированию: . Здесь интегрирование проводится по всему объему тела.

Запишем моменты инерции некоторых тел правильной геометрической формы.

1. Однородный длинный стержень.
Рис. 4.3	Момент инерции относительно оси, перпендикулярной к стержню и проходящей через его середину равен
2. Сплошной цилиндр или диск.
Рис. 4.4	Момент инерции относительно оси, совпадающей с геометрической осью, равен .
3. Тонкостенный цилиндр радиуса R.
Рис. 4.5
4. Момент инерции шара радиуса R относительно оси, проходящей через его центр
Рис. 4.6
5. Момент инерции тонкого диска (толщина b<<R) относительно оси, совпадающей с диаметром диска.
Рис. 4.7
6. Момент инерции бруска
Рис. 4.8
7. Момент инерции кольца
Рис. 4.9

В

Рис. 4.10

ычисления момента инерции здесь достаточно просты, т.к. тело предполагаем однородным и симметричным, а момент инерции определяем относительно оси симметрии.

Для определения момента инерции тела относительно любой оси необходимо воспользоваться теоремой Штейнера.

ОПРЕДЕЛЕНИЕ: Момент инерции J относительно произвольной оси равен сумме момента инерции J_с относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния между осями (рис. 4.10):

J = J_c + ma².