2.3. Вектор скорости. Средняя и мгновенная скорость.

Д

Рис. 2.7

вижения различных тел различаются тем, что тела за одинаковые промежутки (равные) времени проходят различные по величине пути. Для характеристики такого движения вводят понятие скорости.

1) Введем понятие средней скорости () – это величина, равная отношению перемещения к тому промежутку времени, в течение которого это перемещение произошло .

2) За малый промежуток времени t точка проходит путь S, совершая перемещение (рис. 2.6). При t0 отношения и практически перестают изменяться как по величине, так и по направлению и стремятся к определенному пределу

и

который будет выражать вектор мгновенной скорости, т.е. скорости в данный момент времени.

В математике данный предел называется производной, следовательно, скорость можно определить как производную радиус-вектора движущейся точки по времени:

или по модулю .

При бесконечном уменьшении t различие между S и будет уменьшаться и в пределе они совпадут, тогда можно записать, что модуль скорости

, (2.1)

т.е. мгновенная скорость при неравномерном движении численно равна первой производной пути по времени.

Итак, вектор мгновенной скорости в любой точке траектории направлен по касательной к траектории (и совпадает с направлением вектора перемещения) и численно равен первой производной пути по времени.

Единица измерения v: [v]=м/с.

Если рассматривать движение в пространстве, то величину и направление вектора скорости можно представить через проекции этого вектора на направления осей x, y, z (рис. 2.7).

;

где ,

– единичные вектора по осям x, y, z.

Тогда

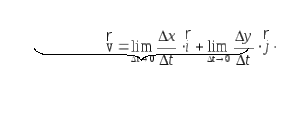
Следовательно,

2.4. Путь при неравномерном движении.

З

Рис. 2.8

а малый промежуток времени t перемещение графически изображается в виде прямоугольника, высота которого равна некоторому значению средней скорости v (рис.2.8). Тогда для любого промежутка времени от 0 до t суммируют все эти элементарные площадки S, т.е. графически эта сумма представляет собой площадь фигуры ABCD (v_ср.t). Чаще всего площадь фигуры дает нам также путь, пройденный при неравномерном движении (математически это записывается как предел).

.

Если v(t) = const, то движение равномерное,

v(t)  const – то движение неравномерное.

2.5. Ускорение. Ускорение при равнопеременном и неравнопеременном прямолинейном движении.

При неравномерном движении необходимо знать закономерность, по которой скорость изменяется со временем. Для этого вводится величина, характеризующая быстроту изменения скорости со временем и называемая ускорением «».

П

Рис. 2.9

усть материальная точка переместилась за малый промежуток времени t из точки А, где она имела скорость в точку В, где скорость (рис.2.9). Приращение скорости точки есть вектор , равный разности конечной и начальной скоростей: .

О

Справка 1.

тношение изменения скорости к промежутку времени, за который это изменение произошло, называется средним ускорением . Это понятие вводится для неравнопеременного движения.

Среднее ускорение направлено также как приращение скорости, т.е. под углом к траектории в сторону ее вогнутости.

В общем случае величина среднего ускорения может быть различной на различных участках траектории и зависеть от величины промежутка времени t, по которому проводится усреднение. В пределе при t  0 точка В будет стремиться к точке А и среднее ускорение по пути АВ превратится в мгновенное или истинное ускорение в точке А.

Поэтому . (2.2)

Итак, мгновенное ускорение движения в любой точке траектории есть вектор, направленный под углом к траектории в сторону ее вогнутости, а по величине равный пределу среднего ускорения при стремлении промежутка времени к нулю.

Из выше приведенных формул следует, что ускорение измеряется в м/с²; [а] = м/с².

По модулю величина ускорения равна 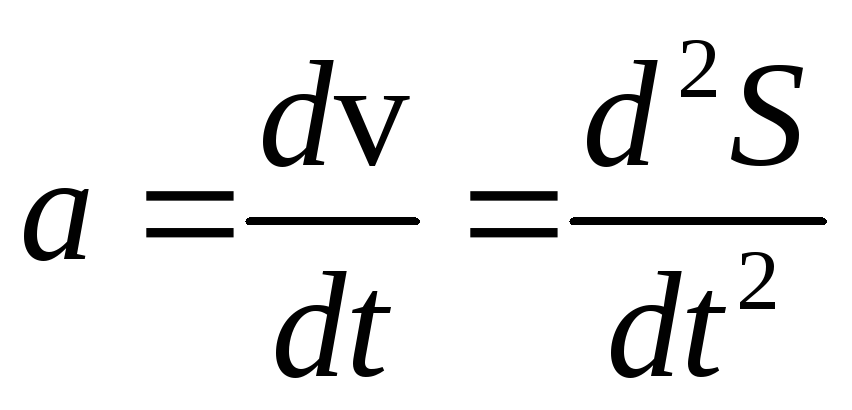. Т.е. величина ускорения определяется первой производной скорости v по времени или второй производной пути по времени.

Если рассматривать движение тела в пространстве, то вектор ускорения можно представить через его проекции на оси X, Y, Z, аналогично как это делали для вектора .

;

Замечание: Следует помнить, что ускорение характеризует не только изменение модуля скорости, но и изменение направления вектора скорости. Например, равномерное движение по окружности является ускоренным из-за изменения направления вектора скорости с течением времени, хотя модуль скорости остается неизменным.

Рассмотрим частный случай ускоренного движения.

Прямолинейное движение с постоянным ускорением называется равноускоренным (a = const). В этом случае мгновенное ускорение будет равно среднему ускорению за любой промежуток времени. И тогда

; (2.3)

Рис. 2.10

В зависимости от поведения скорости со временем различают равноускоренное и «равнозамедленное» движения. Кавычки поставлены, чтобы подчеркнуть, что в любом случае движение происходит с постоянным ускорением.

1. Если а > 0, то движение равноускоренное. Из (2.3) следует, что v=v₀+a(t - t₀) и при t₀ = 0

v=v₀+at

при a > 0 скорость v возрастает. Направления и совпадают.

2. Если a < 0, то движение равнозамедленное и скорость v уменьшается.

Зная зависимость v от t можно подсчитать путь, пройденный телом при равнопеременном движении (рис. 2.10).

Имеем v=v₀ + at, домножим на dt.

dS = v·dt = v₀·dt + a·t·dt.

Интегрируем слева от 0 до S, справа от 0 до t. Получаем, что

.

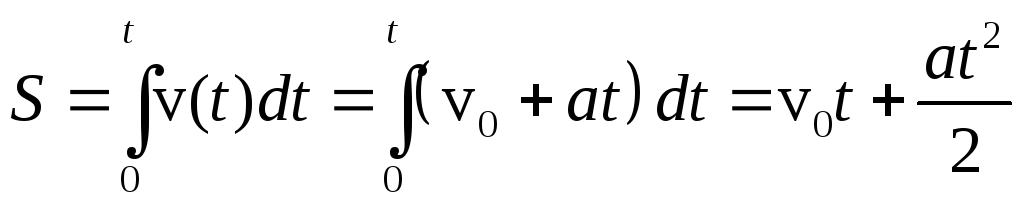Тогда

. (2.4)

Данная формула верна, если за время движения знаки начальной скорости и ускорения совпадают. Наклон прямой v₀+at на рисунке 2.10 зависит от величины «а», чем «а» больше, тем больше угол наклона. «S» численно рано площади заштрихованной фигуры.

ЛЕКЦИЯ 2