3.9. Потенциальное поле сил. Силы консервативные и неконсервативные.

Если частица (тело) в каждой точке пространства подвержена воздействию других тел, то говорят, что эта частица (тело) находится в поле сил.

Пример: 1. Частица вблизи поверхности Земли находится в поле силы тяжести;

2

Рис. 3.4

. Заряженная частице «е» (материальная точка) находится в электрическом поле, возбуждаемом неподвижным точечным зарядом q (рис. 3.4). Это поле характерно тем, что направление силы, действующей на частицу в любой точке пространства, проходит через неподвижный центр (заряд q), а величина силы зависит только от расстояния до этого центра F = F(r).

Поле, обладающее выше указанными свойствами, называется центральным. Поле силы тяжести является частным случаем центрального поля сил (с центром, расположенным на бесконечности).

Если в каждой точке поля сила, действующая на частицу, одинакова по величине и направлению (), такое поле называется однородным.

Поле, не изменяющееся по времени, называется стационарным.

Если для стационарного поля работа сил, совершаемая ими над телом, не зависит от формы и длины траектории, а определяется только начальным и конечным положениями тела в пространстве, то такое поле будем называть потенциальным, а сами силы – консервативными.

И

Рис. 3.5

з независимости работы консервативных сил от пути вытекает, что работа таких сил на замкнутом пути равна нулю. – работа на всем замкнутом пути равна сумме работ, совершаемых на каждом из участков (рис. 3.5). Т.к. изменение направления на обратное приводит к замене на в выражении для работы, то и поскольку работа в потенциальном поле сил не зависит от пути, т.е. , то А=0.

Из равенства нулю работы на замкнутом пути путем обратных рассуждений можно получить, что работа этих сил не зависит от пути.

Поэтому консервативные силы можно определить как такие силы, работа которых на любом замкнутом пути равна «0». А потенциальное поле сил можно определить как поле таких сил, работа которых на любом замкнутом пути рана нулю.

Примеры: сила тяжести – консервативна;

сила трения – неконсервативна;

поле силы тяжести – потенциальное.

3.10. Потенциальная энергия тела в поле сил тяжести (в поле тяготения Земли).

Поле тяготения Земли есть силовое поле, поэтому любое движение тела в силовом поле сопровождается совершением работы силами этого поля.

Для определения потенциальной энергии тела, находящегося в потенциальном поле сил тяжести, посчитаем работу, которую совершают эти силы при движении тела из одной точки в другую. Расчет будем вести в приближении, что поле однородно и сила тяжести постоянна (т.е. у поверхности Земли).

П

Рис. 3.6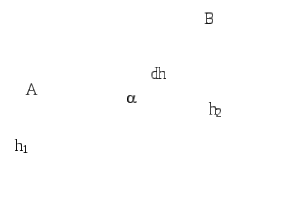

усть тело массой «m» движется по кривой любой формы в поле тяготения Земли (по кривой АВ) (рис. 3.6). На элементарном участке dS работа будет равна .

Из рис. 3.6 следует, что dA=P·dS·cos, но dS·cos=dh, тогда dA=P·dh.

Сила, действующая на тело в любой точке траектории, имеет одинаковую величину P = mg и направление – вниз по вертикали. Поэтому

.

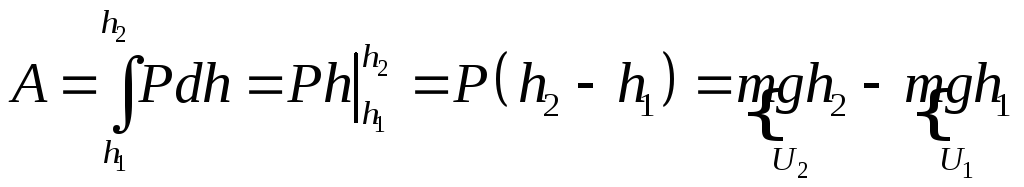В

Рис. 3.7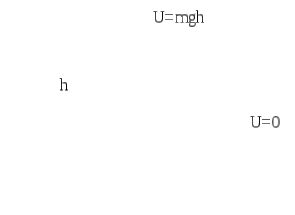

идно, что работа не зависит от формы и длины траектории (т.е. от пути), а определяется только положением начальной и конечной точек траектории движения. Т.е. поле сил тяжести является потенциальным.

Величина

(3.10)

называется потенциальной энергией тела в поле сил тяжести, где h – высота, отсчитанная от уровня, для которого принято U=0.

Поскольку начало отсчета можно принимать произвольно, то потенциальная энергия может иметь отрицательные значения. Если, например, принять за «0» потенциальную энергию тела, находящегося на поверхности Земли, то потенциальная энергия тела, лежащего на дне ямы глубиной , будет равна (рис. 3.7) Отметим, что кинетическая энергия не может быть отрицательной. В рассматриваемом примере мы относили потенциальную энергию U = mgh к телу, находящемуся в поле сил тяжести. Однако, строго говоря, потенциальную энергию следует относить к системе взаимодействующих друг с другом тел. Так, в данном случае U = mgh есть энергия системы Земля - тело. Потенциальная энергия системы тел зависит от их расположения по отношению друг к другу.