
- •1 Оглавление
- •Часть 1
- •Молекулярная физика и термодинамика 84
- •Итоговые задания 130 предисловие
- •В добрый путь, читатель, – удачи!
- •Введение
- •Физическая картина мира
- •Математическое введение Углы
- •Скаляры и векторы
- •Натуральные логарифмы
- •Суммирование
- •Элементы дифференциального исчисления
- •Элементы интегрального исчисления
- •Глава 1 механика
- •Кинематика
- •Механическое движение
- •Вектор перемещения. Путь
- •Скорость
- •Ускорение
- •Равномерное и равнопеременное прямолинейные движения
- •Свободное падение тел
- •Равномерное движение точки по окружности
- •Вращательное движение абсолютно твердого тела вокруг неподвижной оси
- •Динамика движения материальной точки
- •Классическая механика. Границы ее применимости
- •Первый закон Ньютона. Инерциальные системы отсчета
- •Масса и импульс
- •Второй закон Ньютона
- •Третий закон Ньютона
- •Закон сохранения импульса
- •Механический принцип относительности Галилея – Ньютона
- •Силы тяготения
- •Силы упругости
- •Силы трения
- •Элементы динамики вращательного движения абсолютно твердого тела относительно неподвижной оси
- •Момент силы и момент инерции
- •Основной закон динамики вращательного движения
- •Статика
- •Работа и механическая энергия
- •Работа силы при движении материальной точки
- •Механическая энергия
- •Закон сохранения и превращения энергии
- •Мощность
- •Элементы гидроаэромеханики
- •Закон Паскаля
- •Закон Архимеда
- •Давление в движущейся среде
- •Внутреннее трение
- •Основы специальной теории относительности
- •Постулаты Эйнштейна
- •Интервалы длины и времени
- •Закон сложения скоростей
- •Энергия
- •Ответы на вопросы к главе 1
- •Глава 2 молекулярная физика и термодинамика
- •Основы молекулярно-кинетической теории вещества
- •Основные понятия и определения
- •Силы и потенциальная энергия взаимодействия двух молекул
- •О строении газообразных, жидких и твердых тел
- •Молекулярно-кинетическая теория идеальных газов
- •Идеальный газ
- •Распределение Максвелла – Больцмана
- •Распределение Больцмана
- •Средняя длина свободного пробега молекулы
- •Основное уравнение кинетической теории газов
- •Уравнение состояния идеального газа
- •Связь средней кинетической энергии поступательного движения молекул и температуры
- •Реальные газы
- •Свойства жидкостей и твердых тел
- •Поверхностный слой
- •Поверхностное натяжение
- •Лапласово давление
- •Твердое тело
- •Термодинамика
- •Внутренняя энергия системы
- •Внутренняя энергия идеального газа
- •Первое начало термодинамики
- •Калориметрия33
- •Работа газа
- •Цикл Карно. Второе начало термодинамики
- •Некоторые тепловые машины
- •Изменение агрегатного состояния вещества
- •Плавление. Кристаллизация
- •Парообразование. Конденсация. Испарение
- •Свойства паров
- •Кипение
- •Ответы на вопросы к главе 2
- •Итоговые задания
- •Часть 1
- •346500, Г. Шахты, Ростовская обл., ул. Шевченко, 147.
-
Вектор перемещения. Путь
При движении точки положение ее радиус-вектора (рис. 1.3) в пространстве изменяется. Разность
![]()
р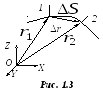 адиус-векторов,
характеризующих конечное (2)
и начальное (1)
положение точки, движущейся в течение
промежутка времени
адиус-векторов,
характеризующих конечное (2)
и начальное (1)
положение точки, движущейся в течение
промежутка времени
![]() ,
называется вектором
перемещения
(перемещением).
Векторы перемещений складываются
геометрически (правило
сложения векторов).
,
называется вектором
перемещения
(перемещением).
Векторы перемещений складываются
геометрически (правило
сложения векторов).
Путь
(![]() или
или
![]() )
является скалярной
величиной, равной длине участка
траектории, пройденного движущейся
точкой за данный промежуток времени.
Пути, пройденные точкой за последовательные
промежутки времени, складываются
арифметически.
График зависимости
)
является скалярной
величиной, равной длине участка
траектории, пройденного движущейся
точкой за данный промежуток времени.
Пути, пройденные точкой за последовательные
промежутки времени, складываются
арифметически.
График зависимости
![]() называется графиком пути.
называется графиком пути.
-
Т

 очка
движется от поверхности Земли вертикально
вверх и по достижении максимальной
высоты Н падает на Землю. Чему в этом
случае равен вектор перемещения и
пройденный точкой путь?
очка
движется от поверхности Земли вертикально
вверх и по достижении максимальной
высоты Н падает на Землю. Чему в этом
случае равен вектор перемещения и
пройденный точкой путь?
-
Скорость
Средней
скоростью
![]() за промежуток времени
за промежуток времени
![]() называется физическая величина, равная
отношению вектора перемещения
называется физическая величина, равная
отношению вектора перемещения
![]() точки к
точки к
![]() :
:
![]() .
.
Направление вектора
средней скорости совпадает с направлением
вектора перемещения
![]() .
.
Скоростью
(мгновенной скоростью, скоростью в
данный момент времени) называется
физическая величина, равная пределу, к
которому стремится средняя скорость
при бесконечном уменьшении промежутка
времени
![]() :
:
![]() .
.
Вектор скорости направлен по касательной к траектории. Направление скорости называют направлением движения точки.
Движение
материальной точки называется равномерным,
если модуль ее мгновенной скорости не
изменяется
![]() .
В противном случае движение называется
неравномерным (или переменным).
.
В противном случае движение называется
неравномерным (или переменным).
Средней
скалярной (средней путевой)
скоростью (![]() )
называется физическая величина,
определяемая отношением
)
называется физическая величина,
определяемая отношением
![]() .
.
В общем
случае средняя скалярная скорость
![]() не равна модулю
не равна модулю
![]() средней скорости тела. Равенство
средней скорости тела. Равенство
![]() =
=![]() выполняется только при прямолинейном
движении материальной точки без изменения
направления движения.
выполняется только при прямолинейном
движении материальной точки без изменения
направления движения.
-
М

 атериальная
точка за промежуток времени Δt
совершает один полный оборот по
окружности радиуса R.
Чему равна средняя и средняя скалярная
скорость точки?
атериальная
точка за промежуток времени Δt
совершает один полный оборот по
окружности радиуса R.
Чему равна средняя и средняя скалярная
скорость точки?
-
Ускорение
Средним
ускорением
![]() называется физическая величина, равная
отношению изменения скорости
называется физическая величина, равная
отношению изменения скорости
![]() точки к длительности промежутка времени
точки к длительности промежутка времени
![]() ,
в течение которого это изменение
произошло:
,
в течение которого это изменение
произошло:
![]() .
.
Направления
векторов
![]() и
и
![]() совпадают.
совпадают.
Ускорением
(мгновенным
ускорением)
материальной точки в момент времени
![]() называется физическая величина
называется физическая величина
![]() ,
равная пределу, к которому стремится
среднее ускорение при бесконечном
уменьшении промежутка времени
,
равная пределу, к которому стремится
среднее ускорение при бесконечном
уменьшении промежутка времени
![]() :
:
![]() .
.
В
данной системе отсчета вектор ускорения
может быть задан проекциями на
соответствующие координатные оси
(проекциями
![]() и
и
![]() ).
).
С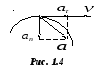 оставляющая
оставляющая
![]() вектора ускорения, направленная вдоль
касательной к траектории в данной точке,
называется тангенциальным
(касательным) ускорением.
Тангенциальное ускорение характеризует
изменение вектора скорости по модулю.
Вектор
вектора ускорения, направленная вдоль
касательной к траектории в данной точке,
называется тангенциальным
(касательным) ускорением.
Тангенциальное ускорение характеризует
изменение вектора скорости по модулю.
Вектор
![]() направлен в сторону движения точки при
возрастании скорости и в противоположную
сторону – при ее убывании.
направлен в сторону движения точки при
возрастании скорости и в противоположную
сторону – при ее убывании.
Составляющая
![]() вектора ускорения, направленная вдоль
нормали к траектории в данной точке,
называется нормальным
ускорением.
Нормальное ускорение характеризует
изменение вектора скорости по направлению
при криволинейном движении.
вектора ускорения, направленная вдоль
нормали к траектории в данной точке,
называется нормальным
ускорением.
Нормальное ускорение характеризует
изменение вектора скорости по направлению
при криволинейном движении.
Величины
![]() и
и
![]() связаны между собой соотношением (рис.
1.4)
связаны между собой соотношением (рис.
1.4)
![]() .
.
При классификации механических движений материальной точки различают четыре основных типа движений:
а) равномерное прямолинейное, б) неравномерное прямолинейное,
в) равномерное криволинейное, г) неравномерное криволинейное.
-
Т

 ри
типа движения характеризуются следующими
кинематическими параметрами: 1.
ри
типа движения характеризуются следующими
кинематическими параметрами: 1.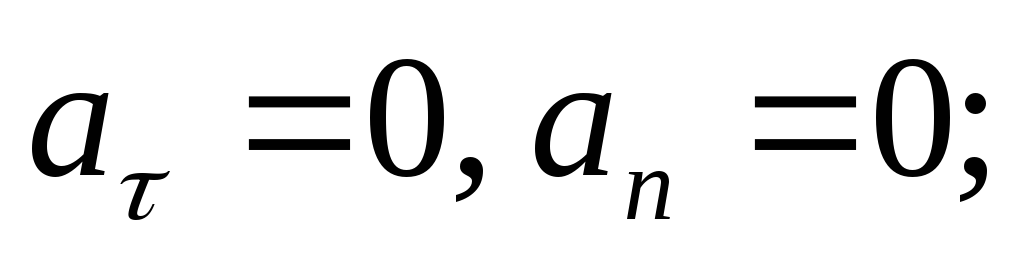 2.
2.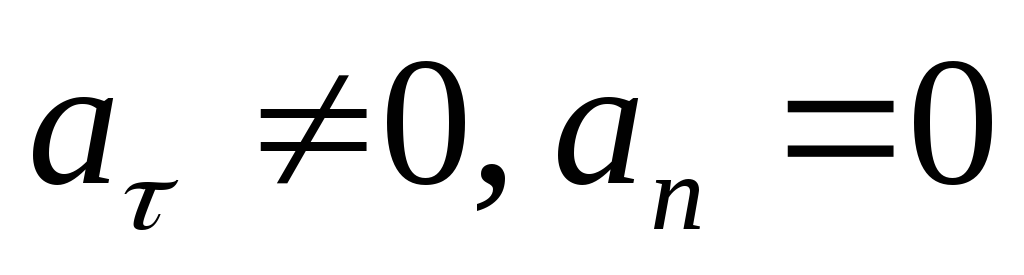 ;
3.
;
3.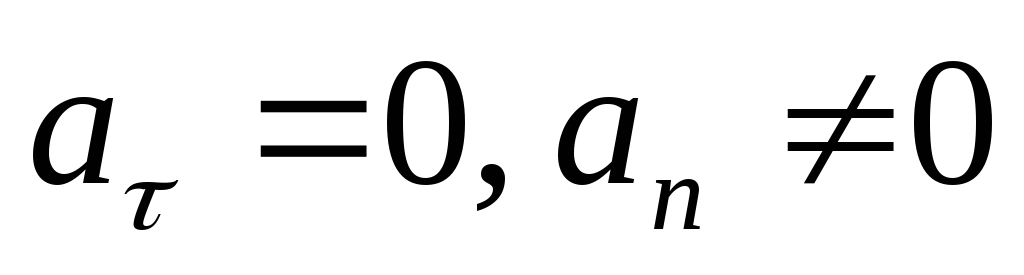 .
Охарактеризуйте каждый из типов
движения.
.
Охарактеризуйте каждый из типов
движения.
