Элементы интегрального исчисления

И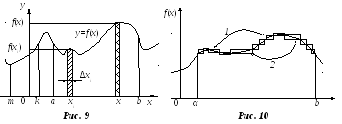 нтегрирование. Пусть заданна функция , график которой изображен на рисунке 9 (функция предполагается непрерывной, дифференцируемой и т.д.; как мы говорили, эти требования для функций, имеющих физический смысл, обычно удовлетворяются). Мы хотим подсчитать, например, площадь криволинейной фигуры, ограниченной прямыми а и b, осью абсцисс и графиком . Заменим график ступенчатой линией с небольшими горизонтальными и вертикальными звеньями. Тогда искомая площадь может быть приближенно представлена суммой площадей полученных прямоугольников. Высота каждого прямоугольника равна , где какая-либо точка достаточно малого интервала . Высота одного прямоугольника больше или меньше высоты другого (соседнего) на величину .

Такое разбиение можно провести множеством способов, два из которых мы опишем (рис. 10). Одна ступенчатая линия лежит целиком над графиком , касаясь его только угловыми точками. Площадь, ограниченную линией 1, осью абсцисс и ординатами точек а и b, обозначим . Она равна . Другая ступенчатая линия лежит целиком под графиком , касаясь его только угловыми точками. Площадь, ограниченную этой линией 2, осью абсцисс и ординатами точек а и b, обозначим . Она равна . В этих формулах n – количество интервалов , которое может быть и различным в описанных разбиениях. Из рисунка 10 видно, что ; больше того, искомая площадь меньше «верхней» площади и больше «нижней» , т.е. . Представим себе теперь, что число ступенек, звеньев неограниченно возрастает, а размеры всех звеньев неограниченно уменьшаются, т.е. совершим предельный переход от конечного к бесконечному числу слагаемых. При этом будет уменьшаться, приближаясь к S сверху (со стороны больших значений), а будет увеличиваться, приближаясь к S снизу (со стороны меньших значений). В пределе (при и ) эти площади сольются друг с другом и с искомой площадью S. Следовательно,

.

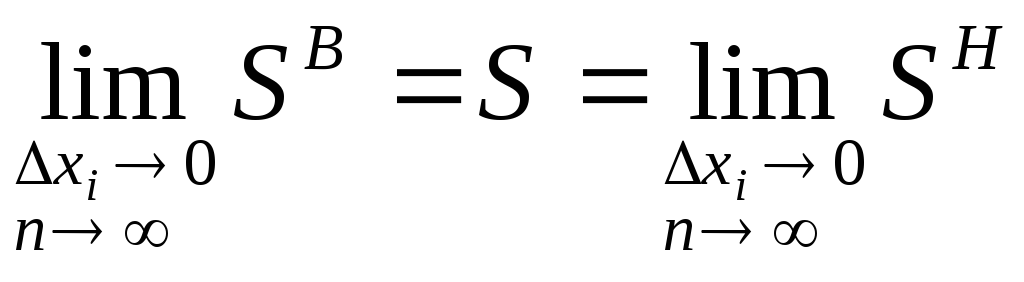Больше того, безразлично, как именно проводилось разбиение, если только высота каждого прямоугольника совпадала с каким-то значением функции на данном интервале . Искомая площадь равна пределу суммы площадей элементарных прямоугольников, когда площадь каждого из них стремится к нулю, а их число неограниченно возрастает:

.

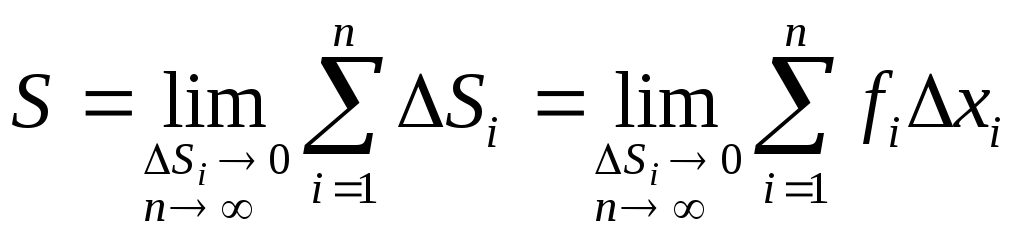В этом пределе удобно от обозначений конечных интервалов перейти к бесконечно малым приращениям dx.

Назовем определенным интегралом сумму бесконечно большого числа бесконечно малых слагаемых:

. (14)

Здесь вместо -го значения функции из заданного интервала – фигурирует – функция в точке х, к которой «стянут» i-й интервал; dx – бесконечно малый интервал значений х около этой точки.

Геометрический смысл определенного интеграла ясен из рисунка 10: это площадь фигуры, которую мы описали. Не надо думать, что так можно определить только площадь. Физический смысл интеграла (14) гораздо шире.

Введем понятие неопределенного интеграла как площади (см. рис. 9), ограниченной функцией , осью абсцисс, ординатой в текущей точке х и ординатой в какой-нибудь неопределенной точке (m, k или какой-то еще). неопределенный интеграл – это определение семейства функций в отличие от определенного интеграла, имеющего конкретное числовое значение. Неопределенный интеграл от функции записывается в виде

(15)

Неопределенный интеграл равен определенному интегралу, нижний предел которого произволен, а верхний – независимая переменная:

где m – произвольная точка оси х. В частности, . Геометрически это площади, ограниченные кривой , осью абсцисс и ординатами точек m и а (первый интеграл) или b (второй интеграл). Разность этих площадей (см. рис. 9) представляет собой определенный интеграл (14) (независимо от положения точки m).

Следовательно, для вычисления определенного интеграла от какой-либо функции надо найти разность значений неопределенного интеграла от этой функции при верхнем и нижнем пределах интегрирования:

. (16)

Еще раз рассмотрим неопределенный интеграл , который равен площади под графиком между ординатами m и x, и дадим ему бесконечно малое приращение

(17)

– так это площадь дважды заштрихованной полоски на рисунке 9. Видим, что действия, обозначенные символами d и , обратны.

Следовательно, неопределенный интеграл это такая функция, производная которой равна подынтегральному выражению. действительно,

(18)

Интегрирование⁶ – это отыскание неопределенного интеграла (по которому можно найти определенный), т.е. функции , производная которой равна подынтегральной функции.

Таким образом, интегрирование – действие, обратное дифференцированию. Правильность интегрирования легко проверить, продифференцировав результат.

В соответствии с правилами дифференцирования, если к неопределенному интегралу прибавить произвольную постоянную, результат не изменится. Неопределенный интеграл находят с точностью до произвольной постоянной интегрирования С.

Приведем результаты интегрирования некоторых элементарных функций, которые Вы можете проверить дифференцированием:

Свойства интеграла

1. Интеграл суммы нескольких функций равен сумме интегралов от этих функций:

2. Постоянный сомножитель можно вынести за знак интеграла:

,

где a=const.