Натуральные логарифмы

Очень важным в математике и физике является предел функции при стремлении х к нулю. Это иррациональное число обозначается буквой е и вычислено с очень большой степенью точности:

(6)

Как известно, логарифмом числа по основанию называется показатель степени х, в которую надо возвести основание, чтобы получить число: . Логарифм записывают в виде

Если в качестве основания логарифмов выбрано число 10, получаются десятичные логарифмы: Примем теперь в качестве основания логарифмов число е. Получим натуральные логарифмы, которые обозначаются Общее правило перехода к логарифму по другому основанию

Для перехода от натуральных логарифмов к десятичным логарифмам положим . Тогда

Модулем этого перехода является натуральный логарифм десяти:

Поэтому для нахождения натурального логарифма числа можно использовать десятичный логарифм:

(с точностью, достаточной для решения задач).

Суммирование

Часто результаты измерений или вычислений представляют собой сумму определенного числа слагаемых. Обозначим все слагаемые суммы какой-нибудь буквой с индексом, который будет изменяться при переходе от одного слагаемого к другому. Например: .

Сложение (суммирование, нахождение разного рода сумм – арифметической, геометрической, алгебраической) обозначают греческой заглавной буквой сигма . Результат суммирования тогда можно записать в виде

Элементы дифференциального исчисления

Производная. Пусть в некоторой непрерывной области значений х существует функция , удовлетворяющая условию дифференцирования, которые мы здесь не рассматриваем. В большинстве интересующих нас физических вопросов эти условия выполняются автоматически. Пример такой функции изображен на рисунке 8.

Введем обозначения: и . Достаточно малый участок кривой между близкими точками 1 и 3 можно представить как отрезок прямой и тем точнее, чем меньше приращение аргумента . Мы получили элементарный треугольник 1 2 3, в котором катетами являются приращение функции и приращение аргумента .

Их отношение характеризует скорость возрастания функции при увеличении аргумента х, зависит от х и интервала .

Устремим это отношение к пределу при , т.е. «стянем» интервал в точку х. При этом и приращение функции (2 3) и приращение аргумента (1 2) устремятся к нулю, т.е. станут бесконечно малыми величинами. Имеем

Этот предел называется первой производной функции .

Пусть, например, задана функция . Ее производная

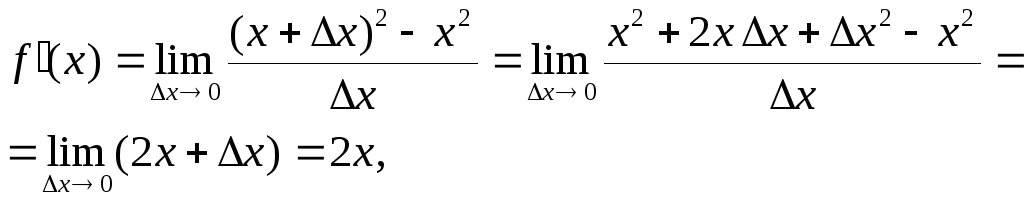
а приращение функции

, т.е. почти равно произведению производной функции и приращения ее аргумента. Следовательно, отношение приращения функции к приращению ее аргумента приблизительно равно производной этой функции и тем точнее, чем меньше приращение аргумента.

Обозначим бесконечно малое приращение d (в отличие от обозначения конечного приращения ). Тогда сколь угодно малое (но не равное нулю!) приращение аргумента будет обозначено dx, соответствующее приращение функции df(x) и .

Аналогичное приближенное равенство справедливо и для других функций. Таким образом, производная

(7)

(с точностью до бесконечно малого слагаемого). При вычислении производных мы часто будем пользоваться последним приближенным равенством.

Как видно из рисунка 8, производная характеризует скорость возрастания функции в точке х. Геометрический смысл производной понятен из рисунка: она равна тангенсу угла наклона касательной к кривой в точке х по отношению к оси абсцисс. Выражение означает, что при возрастании аргумента х функция увеличивается; наоборот, если , то функция уменьшается при возрастании х. Условие

(8)

(касательная параллельна оси абсцисс) есть условие минимума, максимума или точки перегиба, в которой касательная к графику горизонтальна.

Производная представляет собой новую функцию своего аргумента, обычно имеющую конечное значение, хотя пределы числителя и знаменателя в выражении (7) – нули (задав определенное значение аргумента, получим конкретное числовое значение производной).

От нее снова можно взять производную, это будет вторая производная первоначальной функции и т.д. математическое действие, состоящее в нахождении производной от заданной функции, называется дифференцированием⁴.

Свойства производной.

1. Постоянный сомножитель. Если C=const⁵ и , то

(9)

Постоянный сомножитель можно вынести за знак производной.

2. Производная суммы функций. Пусть . тогда

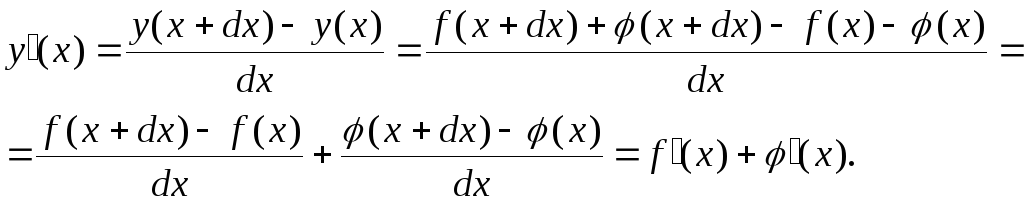(10)

Такое же соотношение справедливо при любом числе слагаемых:

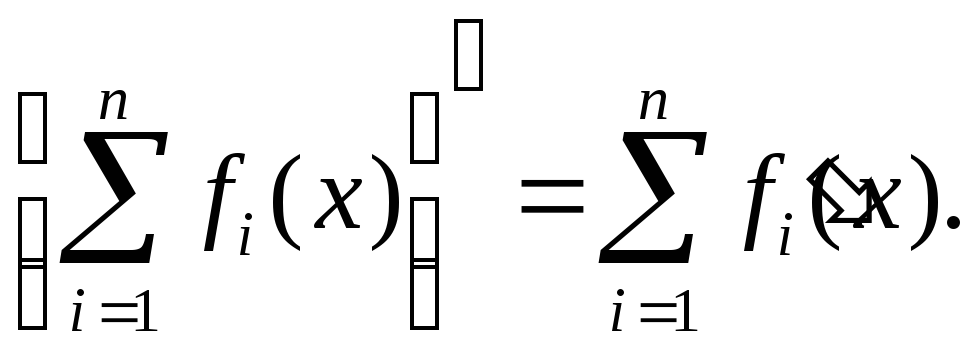(11)

Производная суммы функций равна сумме производных от этих функций.

3. производная произведений от двух функций. Пусть . Производная

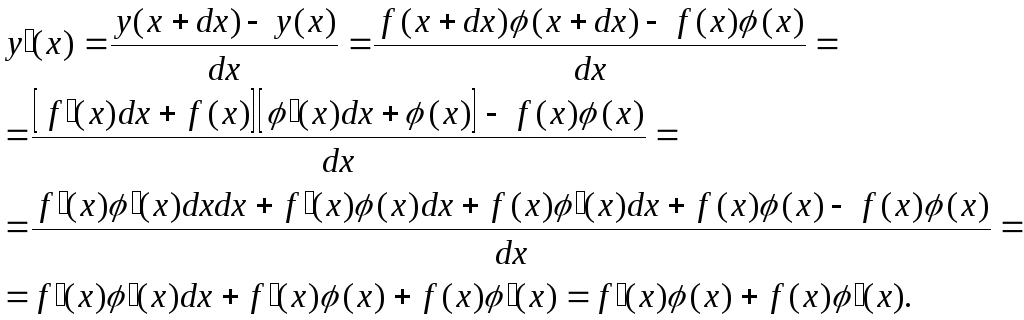
В этом выражении опущено бесконечно малое первое слагаемое (в пределе оно равно нулю). Мы получили

(12)

Производная произведения двух функций равна сумме произведений производной первой функции на вторую и первой функции на производную второй.

4. Производная отношения двух функций. Пусть . Тогда и

Отсюда 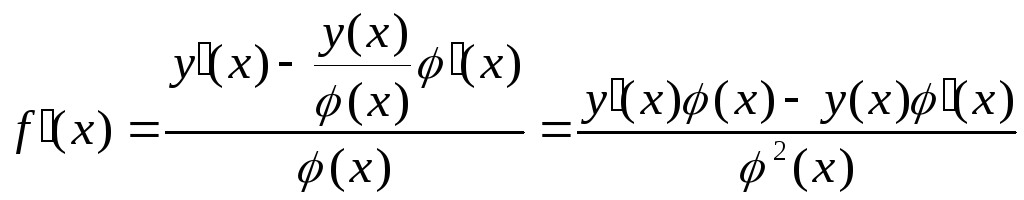. Следовательно,

. (13)

Производная отношения двух функций равна деленной на квадрат знаменателя разности произведений производной числителя на знаменатель и числителя на производную знаменателя (естественно, предполагается, что знаменатель не обращается в нуль).