5. Энергия

Рассмотрим тело, покоящееся в неподвижной системе отсчета, относительно которой подвижная система перемещается со скоростью (рис. 1.38). В математике известно разложение

(для всех ).

Применим его к формуле (1.12):

Пусть скорость подвижной системы не очень велика, чтобы можно было пренебречь членами высших степеней по сравнению с . Тогда

и

Иначе (1.13)

где кинетическая энергия тела в подвижной системе.

Из формулы (1.13) ясно, что выражение

(1.14)

п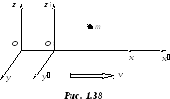 редставляет собой некоторую энергию материальной точки, движущейся со скоростью относительно данной системы отсчета (это энергия рассматриваемой точки в подвижной системе). Ее называют полной энергией материальной точки. Мы получили закон взаимосвязи массы и энергии, установленный Эйнштейном в 1905 г.: всякий объект, масса которого , имеет соответствующую энергию .

В системе отсчета, относительно которой точка покоится, ее кинетическая энергия и полная энергия равна энергии покоя.

Следовательно, полная энергия материальной точки в данной системе отсчета складывается из ее энергии покоя и кинетической энергии. Мы это получили для достаточно медленно движущейся системы; но разность равна кинетической энергии тела и в любой другой движущейся системе отсчета, даже если используемое разложение нельзя оборвать на определенном близком слагаемом, т.е. энергия движения не обязательно равна , как это было в классической механике. Там рассматривалось только первое приближение кинетической энергии, при котором скорость и все члены приведенного разложения, содержащие , пренебрежимо малы. Если же не пренебрегать высшими степенями разложения, то

и кинетическая энергия в общем виде будет представлена рядом:

Естественно, эту энергию удобно считать по формуле (1.13). Закон взаимосвязи массы и энергии (1.14) является одним из основных законов природы. Так, на основе этого подсчитывается энергия ядерных, в частности термоядерных, превращений.

Можно показать, что в изолированной системе тел выполняются законы сохранения, в частности релятивистского импульса и полной энергии (а значит, и релятивистской массы).

Из формулы следует: и , откуда

– величина, инвариантная при изменении системы отсчета.

Следовательно, для тел, имеющих отличную от нуля массу покоя , невозможно движение со скоростью света, при которой импульс тела численно равен . Такое движение со скоростью света не только не возможно, но и единственно возможно для тел, не имеющих массы покоя: . Действительно, , откуда . Такими телами являются фотоны и, может быть, некоторые виды нейтрино.

Массу (релятивистскую!) фотона можно узнать, используя закон взаимосвязи массы и энергии. Как известно, энергия фотона , отсюда

Импульс фотона , отсюда длина волны

Французский физик де Бройль предположил в 1924 г., что такую же длину волны имеет любая частица, импульс которой . Это предположение было блестяще подтверждено опытами по дифракции электронов и привело в дальнейшем к созданию квантовой механики.