2. Интервалы длины и времени

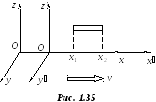
При переходе от одной системы отсчета к другой могут изменяться пространственные и временные характеристики объектов. Мы хотим измерить длину тела, неподвижного в неподвижной системе отсчета (рис.1.35). Для этого нужно зафиксировать координаты и начала и конца тела, причем безразлично когда (тело неподвижно в этой системе отсчета). Длина тела в данной системе

Длину этого же тела в подвижной системе определим как разность координат конца и начала тела, измеренных одновременно :

(разность координат любых точек, измеренных не одновременно в подвижной системе отсчета больше зависит от разновременности, чем от расстояния между этими точками).

В соответствии с преобразованиями Лоренца,

Т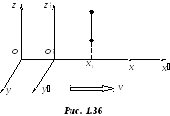аким образом, размеры тела (эталон длины, само пространство) сокращаются в направлении движения:

Исследуем длительность события, например, падения тела, причем координата тела в неподвижной системе не изменяется (, рис. 1.36). Длительность события можно определить, засекая моменты начала и конца этого события в соответствующей системе отсчета: Используя преобразования Лоренца, находим

Следовательно, длительность события в движущейся системе отсчета увеличивается:

Важно представить себе равноправность систем: каждый из наблюдателей «нормально» измеряет «свои» расстояния и времена, но подвижный наблюдатель видит все размеры в неподвижной системе укороченными в направлении движения и все часы в неподвижной системе – отстающими. Неподвижный наблюдатель видит все размеры в подвижной системе укороченными в направлении движения и все часы подвижной системы – отстающими. И бессмысленным является вопрос: а как же на самом деле?

Именно на самом деле укорачиваются размеры в направлении движения и возрастает длительность событий при увеличении скорости движения системы отсчета, в которой рассматриваются объекты. Эти размеры и длительность относительны.

3. Закон сложения скоростей

Пусть материальная точка движется в некоторый момент времени вдоль оси со скоростью относительно неподвижной системы отсчета. Ее скорость в подвижной системе , причем

, а .

Следовательно,

Мы получили закон сложения скоростей в виде:

Легко видеть, что закон сложения скоростей по Галилею есть частный случай этого закона при

Рассмотрим соответствие закона сложения скоростей второму постулату Эйнштейна. Обозначим скорость света в неподвижной системе, относительно которой подвижная система движется с произвольной постоянной скоростью . Скорость света в последней системе

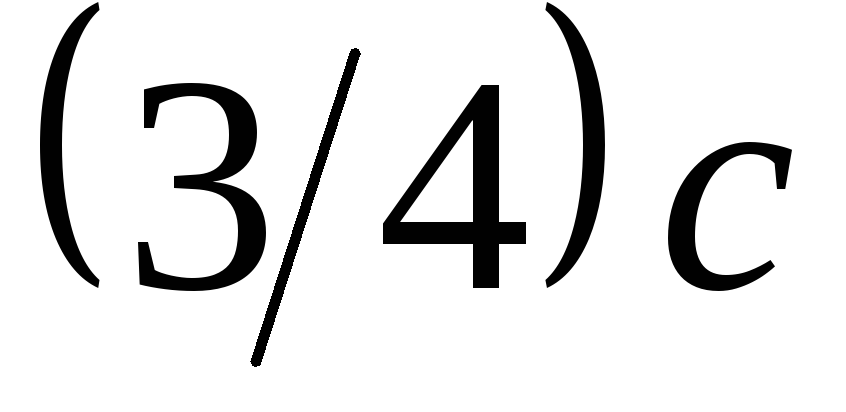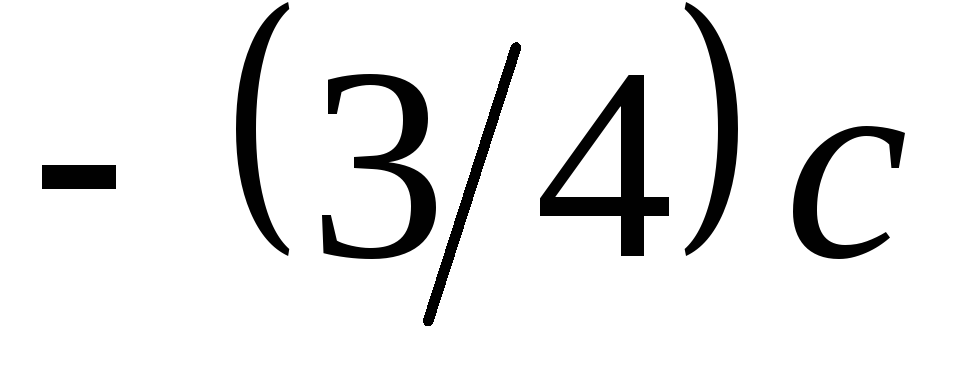31. Пусть два звездолета движутся навстречу друг другу со скоростями и относительно Земли. Какова их скорость сближения

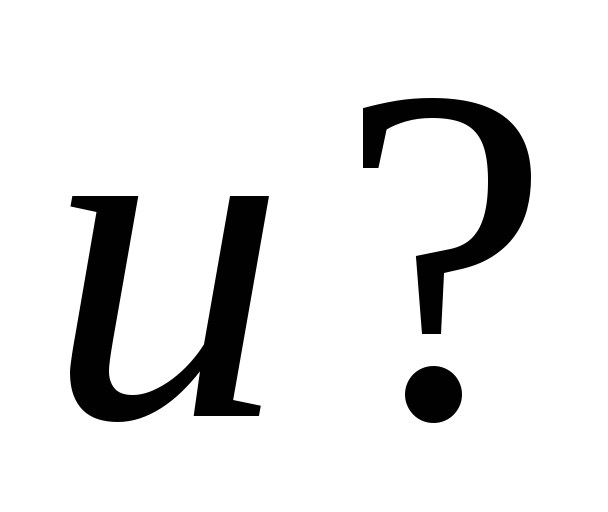
По всем формулам теории относительности видно, что релятивистские эффекты становятся заметными только при движении со скоростью, по порядку величины приближающейся к скорости света.

4. Масса

С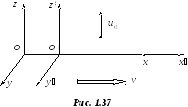нова рассмотрим две инерциальные системы отсчета (рис. 1.37), причем подвижная система движется относительно неподвижной со скоростью ~.

Пусть материальная точка движется вдоль оси в неподвижной системе отсчета со скоростью Тогда масса точки практически равна ее массе покоя , а импульс (т.е. направлен вдоль оси ). В подвижной системе отсчета импульс той же материальной точки имеет другое значение и направление, но его проекция на ось равна проекции импульса на ось : .

Действительно в процессе установления скорости должны были действовать силы, изменяющие импульс точки по второму закону Ньютона только в направлении этой скорости, т.е. вдоль оси . Следовательно, составляющие импульса, перпендикулярные осям и , не изменились: , где масса той же точки в подвижной системе отсчета – ее релятивистская масса.

Проекция скорости материальной точки на ось

,

где перемещение вдоль оси , перпендикулярной скорости движения системы, его величина не зависит от скорости . Время движения по этому отрезку , значит, скорости и неодинаковы.

Релятивистская масса

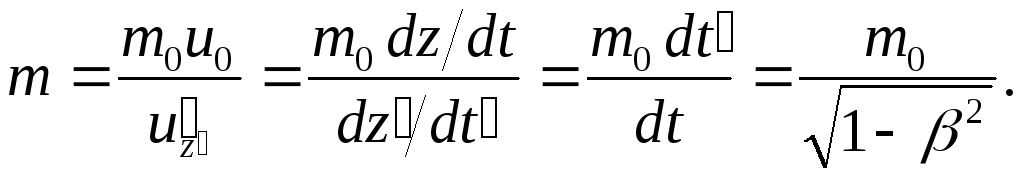
Таким образом, масса тела в движущейся системе отсчета

(1.12)

т.е. больше массы покоя, и только при движении с достаточно малыми скоростями может считаться не зависящей от скорости. Последняя формула многократно подтверждена опытами на ускорителях, где массы частиц увеличиваются в десятки раз.