3. Элементы динамики вращательного движения абсолютно твердого тела относительно неподвижной оси

   1. Момент силы и момент инерции

Основной задачей динамики вращательного движения является определение угловых координат точек вращающегося тела в любой момент времени по известным начальным угловым координатам, угловым скоростям и по заданным моментам внешних сил, действующих на тело.

Абсолютно твердое тело, имеющее закрепленную ось вращения, без воздействия моментов внешних сил не изменяет скорости вращательного движения. Если, например, к телу с осью вращения (рис. 1.16) в точке , находящейся на расстоянии от оси вращения, приложена внешняя сила , то ее составляющая , лежащая в плоскости, перпендикулярной к оси вращения, и перпендикулярная к радиусу точки приложения внешней силы, приводит к изменению вращательного движения тела. Составляющие и (рис. 1.16) не влияют на вращательное движение, а способны лишь вызвать ускорение поступательного движения или деформацию тела.

Плечом силы относительно оси называется кратчайшее расстояние d от оси вращения до линии действия силы. На рисунке 1.17 показаны плечи d₁, d₂ и d₃ сил и , приложенных к телу в точках 1, 2 и 3 (ось вращения перпендикулярна плоскости рисунка и проходит через точку О).

Моментом силы называется векторная величина , модуль которой определяется выражением:

,

где – модуль приложенной к телу силы;

d – плечо этой силы относительно данной оси.

м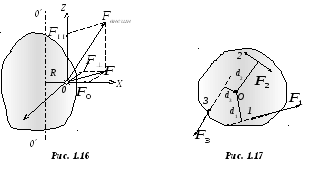 омент силы совпадает с осью вращения, а его направление определяется по правилу правого винта.

Суммарный момент нескольких сил, действующих на тело, равен алгебраической сумме моментов всех сил относительно данной оси:

.

При этом моменты сил, вращающие тело вокруг данной оси по часовой стрелке и против, берутся с разными знаками. Например, моменты сил и (рис. 1.17) считаются положительными, а момент силы – отрицательным.

19. Как Вы думаете, почему дверная ручка располагается именно в этом месте двери?

20. Почему канатоходец для равновесия использует длинный тонкий шест?

Моментом инерции материальной точки относительно данной оси называется скалярная величина , равная произведению массы точки на квадрат ее расстояния от оси:

.

Моментом инерции тела относительно оси называется величина , равная сумме моментов инерции всех точек тела, массами , на которые оно разбивается:

.

Причем это выражение тем точнее, чем больше и меньше , т.е.

.

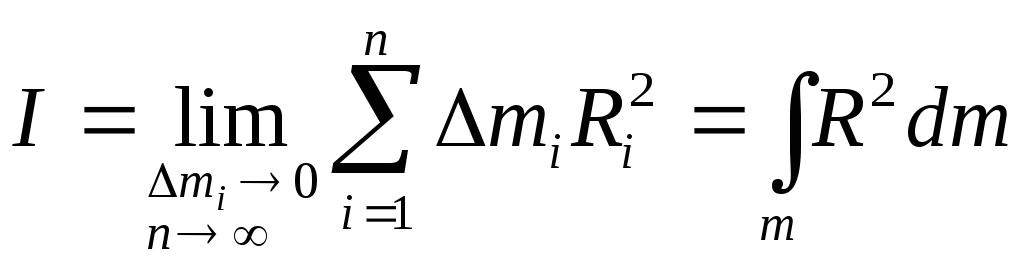Момент инерции является мерой инертности тела при вращательном движении. Он играет такую же роль, что и масса при описании поступательного движения. Но если масса данного тела в задачах ньютоновской механике считается величиной постоянной, то момент инерции данного тела зависит от распределения его массы относительно оси вращения.

Моменты инерции некоторых однородных тел простейшей формы (т – масса тела)
Сплошной шар радиуса R, ось вращения проходит через центр масс шара
Сплошной цилиндр (диск) радиуса R, ось вращения совпадает с продольной осью цилиндра и проходит через центр масс
Полый тонкостенный цилиндр (обруч) радиуса R, ось вращения совпадает с продольной осью цилиндра и проходит через центр масс
Прямолинейный тонкий стержень длинной l, ось вращения перпендикулярна к продольной оси стержня и проходит через центр масс
Прямолинейный тонкий стержень длинной l, ось вращения перпендикулярна к продольной оси стержня и проходит через конец стержня

21. Объясните: почему моменты инерции для стержня относительно осей, показанных в таблице (пункты 4 и 5) различны?