
- •Лекция 1 предел последовательности
- •1 Понятие числовой последовательности. Предел числовой последовательности. Свойства сходящихся числовых последовательностей
- •Свойства сходящихся последовательностей
- •2 Бесконечно большие и бесконечно малые числовые последовательности. Основные способы вычисления пределов
- •Свойства бесконечно больших и бесконечно малых последовательностей:
- •Основные способы вычисления пределов:
- •Лекция 2 предел функции
- •1 Предел функции в точке. Односторонние пределы. Предел функции в бесконечности
- •2 Бесконечно малые и бесконечно большие функции. Замечательные пределы
- •Свойства бесконечно малых и бесконечно больших функций
- •Первый и второй замечательные пределы
- •3 Непрерывность функции в точке и на отрезке. Точки разрыва функции и их классификация
- •Свойства функций, непрерывных в точке:
- •Непрерывность функции на отрезке
- •Свойства функций, непрерывных на отрезке
- •Точки разрыва функции и их классификация
- •Лекция 3 производная функции
- •1 Производная функции, ее геометрический и экономический смысл. Основные правила дифференцирования. Производные основных элементарных функций
- •Основные правила дифференцирования
- •2 Логарифмическое дифференцирование. Производная неявной функции. Производные высших порядков
- •Лекция 4 правило лопиталя. Дифференциал функции
- •1 Раскрытие неопределенностей при помощи правила Лопиталя
- •2 Дифференциал функции, его геометрический смысл. Применение дифференциала в приближенных вычислениях
- •Лекция 5 исследование функций
- •1 Локальные экстремумы функции. Достаточные условия экстремума функции
- •2 Исследование функций на выпуклость и вогнутость. Точка перегиба
- •3 Асимптоты графика функции
- •4 Общая схема построения графика функции
- •Лекция 6 функции нескольких переменных
- •1 Предел и непрерывность функции двух переменных
- •2 Частные производные первого порядка. Полный дифференциал. Частные производные высших порядков
- •3 Экстремум функции нескольких переменных. Необходимые и достаточные условия существования экстремума
- •Лекция 7 НеоПределенный иНтеграл
- •1 Первообразная и неопределенный интеграл. Таблица основных неопределенных интегралов
- •Основные свойства неопределенного интеграла
- •2 Основные методы интегрирования
- •Лекция 8 НеоПределенный иНтеграл (продолжение)
- •1 Интегрирование выражений, содержащих квадратный трехчлен
- •2 Интегрирование простейших рациональных дробей. Интегрирование простейших иррациональных функций
- •Интегрирование простейших иррациональных функций
- •3 Интегрирование тригонометрических функций
- •Лекция 9 оПределенный иНтеграл
- •1 Определенный интеграл и его геометрический смысл. Основные свойства определенного интеграла
- •Геометрический смысл определенного интеграла
- •Основные свойства определенного интеграла
- •Формула Ньютона-Лейбница
- •2 Основные способы вычисления определенного интеграла Замена переменной в определенном интеграле
- •Интегрирование по частям
- •Доказательство
- •3 Вычисление площадей плоских фигур, объемов тел вращения, длин дуг плоских кривых Площадь криволинейной трапеции
- •Объем тела вращения
- •Длина дуги плоской кривой
- •Лекция 10 несобственные интегралы
- •1 Несобственные интегралы с бесконечными пределами интегрирования
- •2 Несобственные интегралы от неограниченных функций
- •Лекция 11 дифференциальные уравнения первого порядка
- •1 Дифференциальные уравнения первого порядка. Задача Коши
- •2 Дифференциальные уравнения с разделяющимися переменными
- •3 Линейные дифференциальные уравнения первого порядка
- •1 Метод подстановки (метод Бернулли).
- •2 Метод вариации произвольной постоянной (метод Лагранжа)
- •Лекция 12 дифференциальные уравнения высших порядков
- •1 Интегрирование дифференциальных уравнений высших порядков, допускающих понижение порядка
- •2 Однородные и неоднородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Лекция 13 числовые ряды
- •Числовой ряд. Сходимость. Признаки сходимости
- •1 Определение числового ряда. Сходимость. Основные свойства числовых рядов
- •Основные свойства числовых рядов
- •2 Ряды с положительными членами. Признаки сходимости
- •3 Знакочередующиеся и знакопеременные ряды
- •Лекция 14 степенные ряды
- •Ключевые понятия
- •1 Определение степенного ряда. Теорема Абеля
- •2 Свойства степенных рядов
- •3. Ряды Тейлора, Маклорена для функций
- •Разложение некоторых элементарных функций в ряд Маклорена
- •Приложения степенных рядов
- •Список литературы
- •Содержание
- •Лекция 13 Числовые ряды………….……………………………………..93
- •Лекция 14 Степенные ряды……………………...……….………………103
- •Список литературы…………..…………….……...………………………..112
- •220086, Минск, ул. Славинского, 1, корп. 3.
Лекция 4 правило лопиталя. Дифференциал функции
План
1 Раскрытие неопределенностей при помощи правила Лопиталя.
2 Дифференциал функции, его геометрический смысл. Применение дифференциала в приближенных вычислениях.
Ключевые понятия
Правило Лопиталя.
Дифференциал функции.
Раскрытие неопределенностей.
1 Раскрытие неопределенностей при помощи правила Лопиталя
При вычислении пределов функции часто возникают неопределенности следующих видов:
![]()
Раскрыть эти неопределенности помогает правило Лопиталя. Пусть функции f(x) и g(x) имеют производные в окрестности точки х0. Тогда:
-
Если
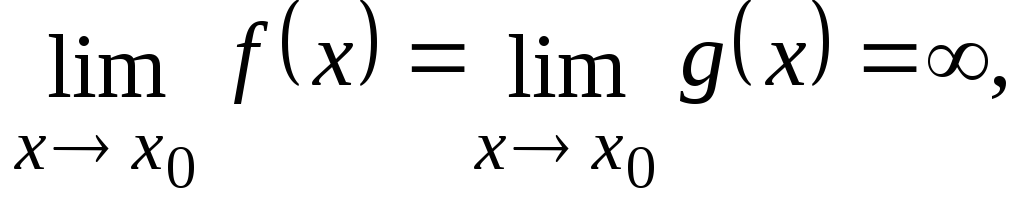 то
то
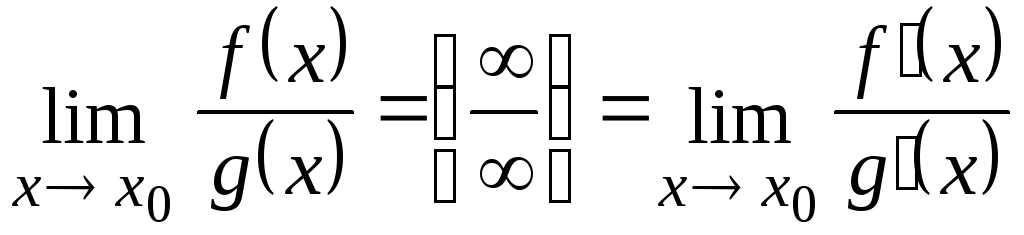 ,
при условии, что последний предел
существует.
,
при условии, что последний предел
существует. -
Если
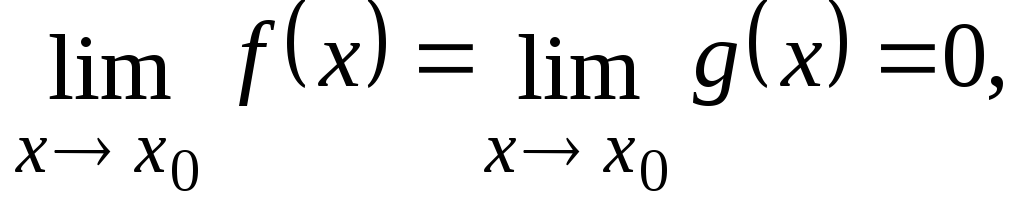 то
то
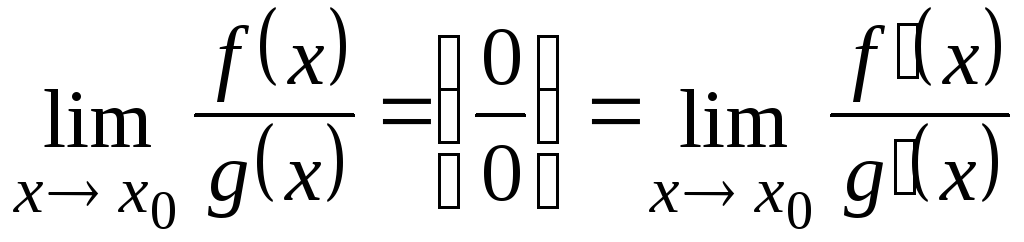 ,
при условии, что последний предел
существует.
,
при условии, что последний предел
существует.
Следовательно,
если мы имеем неопределенности
![]() воспользоваться правилом Лопиталя
означает найти
производные числителя и знаменателя,
а затем вычислить новый предел.
воспользоваться правилом Лопиталя
означает найти
производные числителя и знаменателя,
а затем вычислить новый предел.
Пример 1:
а)
![]() ;
;
б)
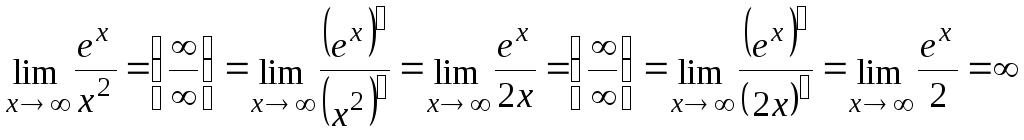 ;
;
в)
![]()
так
как
![]() (первый замечательный предел).
(первый замечательный предел).
Рассмотрим остальные неопределенности:
1)
![]() .
Пусть
.
Пусть
![]() ,
тогда
,
тогда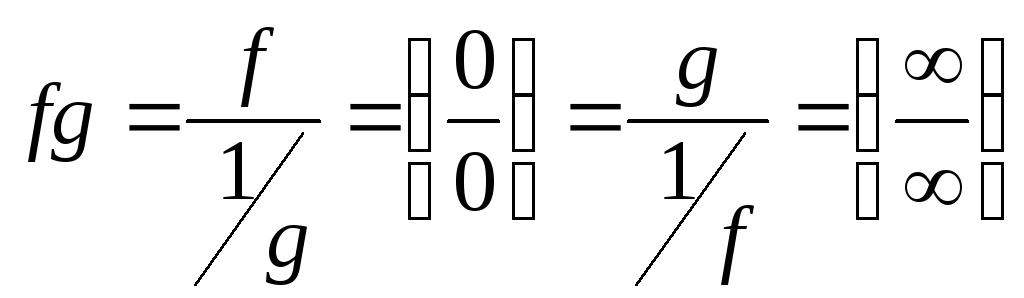 ,
т. е. мы свели данную неопределенность
к
,
т. е. мы свели данную неопределенность
к
![]() или
или
![]() ,
после чего можно применять правило
Лопиталя;
,
после чего можно применять правило
Лопиталя;
2)
![]() ,
тогда
,
тогда
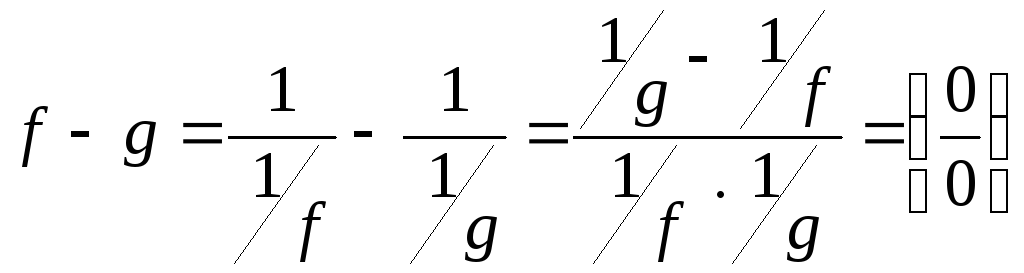 ;
;
3)
![]() .
Данные неопределенности также сводятся
к неопределенностям
.
Данные неопределенности также сводятся
к неопределенностям
![]() или
или
![]() .
Для этого можно воспользоваться формулой
.
Для этого можно воспользоваться формулой
![]()
Так,
если
![]() то получаем неопределенность
то получаем неопределенность
![]() (так как
(так как
![]() ,
после чего можно получить
,
после чего можно получить
![]() или
или
![]() (смотри выше).
(смотри выше).
Пример 2
а)
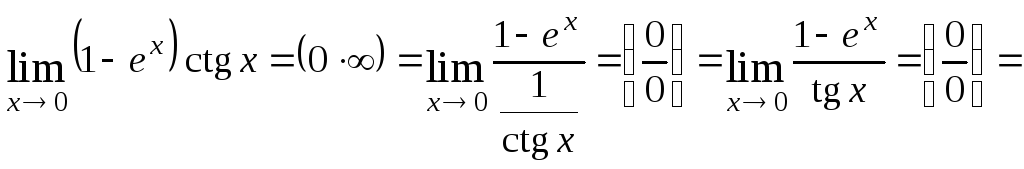
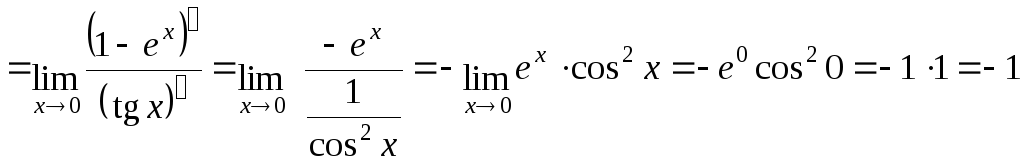 ;
;
б)
![]()
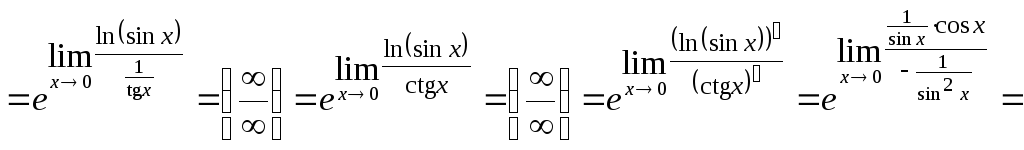
![]() .
.
2 Дифференциал функции, его геометрический смысл. Применение дифференциала в приближенных вычислениях
Определение 1 Функция f (х) называется дифференцируемой в точке х0, если ее приращение в этой точке можно представить в виде
![]() (1)
(1)
где А
![]() R,
(Δх)
– бесконечно малая функция более
высокого порядка малости, чем Δх
при Δх
→ 0, т.е.
R,
(Δх)
– бесконечно малая функция более
высокого порядка малости, чем Δх
при Δх
→ 0, т.е.
![]() .
.
Теорема: для того, чтобы функция f (x) была дифференцируемой в точке х0, необходимо и достаточно, чтобы в точке х0 существовала производная f(x0) = А.
Следовательно, из формулы (1) имеем
![]() .
(2)
.
(2)
Определение
2 Функция
![]() (от х)
есть главная
линейная часть приращения функции
f (x)
в точке х0.
Эту главную линейную часть приращения
функции f (x)
и называют дифференциалом
функции f (x)
в точке х0
и обозначают
(от х)
есть главная
линейная часть приращения функции
f (x)
в точке х0.
Эту главную линейную часть приращения
функции f (x)
и называют дифференциалом
функции f (x)
в точке х0
и обозначают
![]() (3)
(3)
В
частности, для f (x)
= х
имеем
![]()
Следовательно, из формулы (3) получаем:
![]() .
(4)
.
(4)
Выясним геометрический смысл дифференциала (см. рисунок):
ВД
= ВС + СД;
ВД
=
![]() ВС
=
ВС
=
![]() А
=
=
А
=
=
![]() ,
так как АВ
=
,
так как АВ
=
![]() ,
,
![]() А
=
А
=
![]() .
.
Следовательно,
из уравнения (2) имеем СД
= α(![]() ).
).
Таким
образом, ВС
=
![]()
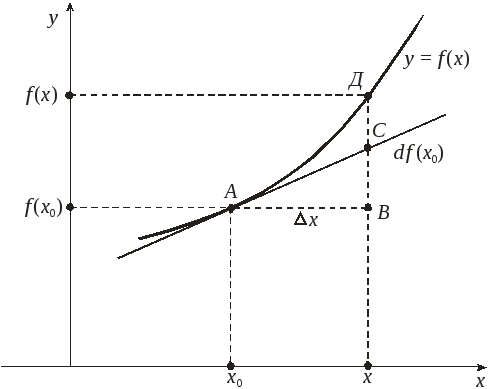
Следовательно,
с геометрической
точки зрения,
дифференциал функции равен приращению
ординаты касательной, проведенной к
графику функции в точке с абсциссой
х0,
при приращении аргумента
![]() .
.
Для дифференциалов функций f и g справедливы формулы, подобные формулам для производных функций:
1)
![]() ;
;
2)
![]() ;
;
3)
![]()
Пример 3 Найти дифференциалы функций:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]()
![]() .
.
Заметим,
что dx
= d(x
+ c),
с
![]() R,
d(ax
+ в) = adx
dx
=
R,
d(ax
+ в) = adx
dx
=
![]()
Данные формулы будут широко применяться при вычислении интегралов функций. С помощью дифференциала можно также приближенно вычислить значения функции f для х, близких к х0. Так, отбросив бесконечно малую функцию в формуле (2), получаем
![]() .
(5)
.
(5)
Пример 4 Вычислить приближенно:
а)
![]() ;
б)
;
б)
![]() .
.
Решение. Воспользуемся формулой (5):
а)
![]() ;
;
х0
= 64,
![]() = 0,05;
= 0,05;
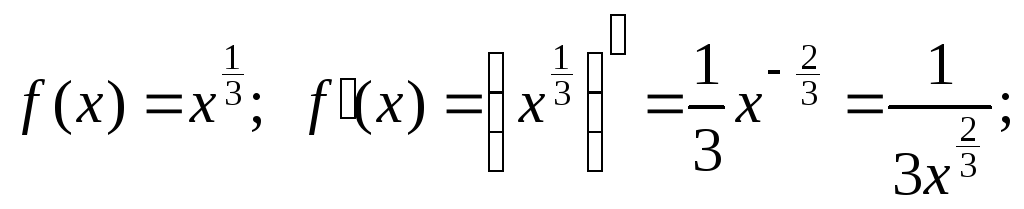
![]()
![]()
Следовательно,
![]()
Заметим,
что
![]() ;
;
б)
![]()
![]()
![]()
![]()
![]()
Заметим,
что
![]()
