2 Несобственные интегралы от неограниченных функций

Пусть функция непрерывна на конечном промежутке , но неограничена при x  b – 0, т.е. .

Определение 2 Несобственным интегралом от функции у=f(x) на промежутке называется предел , т.е.

. (4)

Если предел, стоящий в правой части равенства (4), конечный, то несобственный интеграл называется сходящимся, в противном случае – расходящимся. Интеграл (4) иногда называют несобственным интегралом II рода.

Аналогично вводится понятие несобственного интеграла от функции непрерывной, но не ограниченной на промежутке :

. (5)

Если функция не ограничена при , где , и непрерывна при и , то несобственный интеграл от функции у=f(x) на отрезке обозначается и определяется равенством

. (6)

Несобственный интеграл (6) называется сходящимся, если сходятся оба несобственных интеграла в правой части равенства (6). В противном случае данный интеграл называется расходящимся.

Пример 2 Исследовать на сходимость несобственные интегралы:

а) ; б) .

Решение: а) данный интеграл является интегралом от неограниченной функции (подынтегральная функция не определена в точке , при эта функция неограниченно возрастает).

По определению 2 имеем

[замена: ] = ,

следовательно, данный интеграл сходится;

б) по формуле 5

.

Значит, данный интеграл является расходящимся.

Лекция 11 дифференциальные уравнения первого порядка

План

1 Дифференциальные уравнения первого порядка. Задача Коши.

2 Дифференциальные уравнения с разделяющимися переменными.

3 Линейные дифференциальные уравнения первого порядка.

Ключевые понятия

Дифференциальное уравнение. Порядок дифференциального уравнения. Интегральная кривая. Общее и частное решения дифференциального уравнения. Общий и частный интегралы дифференциального уравнения.

Задача Коши. Уравнение с разделяющимися переменными. Линейные дифференциальные уравнения. Метод подстановки. Метод вариации произвольной постоянной.

1 Дифференциальные уравнения первого порядка. Задача Коши

Определение 1 Уравнение

,

(1)

связывающее независимую переменную х, неизвестную функцию и ее производные (наличие хотя бы одной производной обязательно), называется дифференциальным уравнением.

Если уравнение (1) можно записать в виде

,

(2)

где f – известная функция, то будем говорить, что дифференциальное уравнение разрешено относительно старшей производной . Оно называется дифференциальным уравнением в нормальной форме.

Определение 2 Дифференциальное уравнение, в котором неизвестная функция у зависит от одной переменной х, называется обыкновенным (ОДУ). Если же дифференциальное уравнение содержит неизвестную функцию нескольких переменных и ее частные производные, то оно называется уравнением в частных производных.

Определение 3 Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение.

Определение 4 Решением (интегралом) дифференциального уравнения n-го порядка называется любая функция, которая задана на промежутке, имеет на этом промежутке производную порядка n и обращает уравнение в верное равенство в каждой точке данного промежутка.

Определение 5 График решения дифференциального уравнения называется интегральной кривой.

Процесс нахождения решения дифференциального уравнения называется интегрированием этого уравнения. Решение может быть задано в неявном виде . В этом случае его называют интегралом дифференциального уравнения.

Определение 6 Общим решением дифференциального уравнения (1) называется функция

,

(3)

зависящая от х и n произвольных независимых постоянных , обращающая это уравнение в тождество при любых значениях . Заметим, что число произвольных постоянных равно порядку дифференциального уравнения.

Определение 7 Общее решение, заданное в неявном виде

,

называется общим интегралом.

Определение 8 Частным решением дифференциального уравнения (1) называется решение, которое получается из формулы (3), если придать определенные значения произвольным постоянным, т. е.

,

где – фиксированные числа.

Определение 9 Частным интегралом называется интеграл, полученный из общего путем фиксирования произвольных постоянных

,

где – фиксированные числа.

В некоторых случаях дифференциальное уравнение может не иметь решения. Поэтому есть ряд теорем существования, которые накладывают условия на правую часть дифференциального уравнения, при выполнении которых решение существует.

Общий вид дифференциального уравнения первого порядка:

.

(4)

Если это уравнение разрешимо относительно , то

.

(5)

Следовательно, общим решением дифференциального уравнения (4) называется функция

,

зависящая от х и произвольной постоянной С, обращающая это уравнение в тождество.

Общее решение, заданное в неявном виде

,

называется общим интегралом.

Геометрически общее решение представляет собой семейство интегральных кривых на плоскости, зависящих от одного параметра С. Частное решение и частный интеграл имеют соответственно вид:

; .

Уравнение имеет бесконечное число решений. Чтобы из этого множества решений выделить одно, т. е. частное решение, надо задать некоторые дополнительные условия. Таким условием, определяющим частное решение, является начальное условие, или условие Коши:

,

(6)

где х₀ – заданный элемент из области определения.

Задача отыскания частного решения уравнения (5), удовлетворяющего начальному условию (6), называется задачей Коши для этого уравнения.

Рассмотрим простейшее дифференциальное уравнение первого порядка

,

(7)

где – непрерывная на некотором промежутке функция.

Решение ОДУ (7) находится интегрированием его левой и правой частей:

.

Пример 1 Решить уравнение и построить семейство интегральных кривых.

Решение. – общее решение данного уравнения, где С = const.

Задавая конкретные значения постоянной С, будем иметь частные решения исходного уравнения.

Таким образом, интегральные кривые – это множество парабол. Построим их:

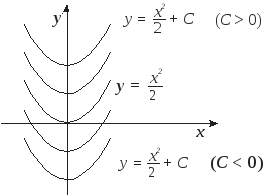
Если для данного уравнения задана задача Коши, т. е. необходимо найти решение исходного уравнения, удовлетворяющего начальному условию, например:

,

то для ее решения необходимо в общее решение задачи вместо х и у подставить , и найти конкретное значение произвольной постоянной С. Так как , то .

Следовательно, решением данной задачи Коши будет функция

.

Заметим, что график этой функции проходит через точку .

С геометрической точки зрения, решить задачу Коши – значит, из бесконечного множества интегральных кривых найти ту, которая проходит через точку с координатами .

Пример 2 Решить задачу Коши

, .

Решение:

;

– общее решение данного уравнения.

Для решения задачи Коши найдем константу С. Подставим в общее решение , :

.

Таким образом, решением задачи Коши будет функция

.

Следовательно, интегральная кривая имеет вид: