Частный институт управления и предпринимательства

В. М. Метельский

Ю. В. Минченков

М. И. Овсеец

Е. М. Светлая

ВЫСШАЯ МАТЕМАТИКА

ОСНОВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА

Учебно-методическое пособие

М

инск 2010

УДК 51

ББК 22.1

М 54

Рекомендовано к изданию редакционно-издательским советом Частного института управления и предпринимательства

А в т о р ы:

доцент кафедры высшей математики и статистики

Частного института управления и предпринимательства

кандидат физико-математических наук В. М. Метельский;

заведующий кафедрой высшей математики и статистики

Частного института управления и предпринимательства

кандидат физико-математических наук, доцент Ю. В. Минченков;

профессор кафедры высшей математики и статистики

Частного института управления и предпринимательства

кандидат физико-математических наук, доцент М. И. Овсеец;

старший преподаватель кафедры высшей математики и статистики

Частного института управления и предпринимательства Е. М. Светлая

Р е ц е н з е н т ы:

доцент кафедры высшей математики и математической физики БГУ

кандидат физико-математических наук, доцент А.А. Егоров;

доцент кафедры экономики и управления бизнесом ГИУСТ БГУ

кандидат физико-математических наук, доцент Н.Н. Рачковский

Рассмотрено и одобрено на заседании

кафедры высшей математики и статистики,

протокол № 7 от 12.02.2010 г.

Метельский, В. М.

М 54 Высшая математика. Основы математического анализа: учеб. – метод. пособие / В.М. Метельский [и др.]. – Минск: Частн. ин-т упр. и предпр., 2010. – 115 с.

ISBN 978-985-6971-08-5.

Подготовлено в соответствии с рабочей программой ЧИУиП данной дисциплины, стандартом и типовой программой Минобразования Республики Беларусь. Содержит лекции по математическому анализу и дифференциальным уравнениям.

Предназначено для студентов Частного института управления и предпринимательства.

УДК 51

ББК 22.1

© Метельский В.М., Минченков Ю.В., Овсеец М.И., Светлая Е.М., 2010

ISBN 978-985-6971-08-5 © Частный институт управления и предпринимательства, 2010

Лекция 1 предел последовательности

План

1. Понятие числовой последовательности. Предел числовой последовательности. Свойства сходящихся числовых последовательностей.

2. Бесконечно большие и бесконечно малые числовые последовательности. Основные способы вычисления пределов.

Ключевые понятия

Бесконечная числовая последовательность.

Предел бесконечной числовой последовательности.

Бесконечно большие числовые последовательности.

Бесконечно малые числовые последовательности.

Монотонные последовательности.

Второй замечательный предел.

1 Понятие числовой последовательности. Предел числовой последовательности. Свойства сходящихся числовых последовательностей

Определение 1 Бесконечной числовой последовательностью (последовательностью) называется числовая функция

(1)

определенная на множестве натуральных чисел N. Каждое значение называют элементом (или членом) последовательности, а число п – номером элемента последовательности. Заметим, что последовательность всегда содержит бесконечное число членов. Числовую последовательность будем обозначать .

Приведем примеры числовых последовательностей:

1. ;

2. ;

3. ;

4. ;

5. .

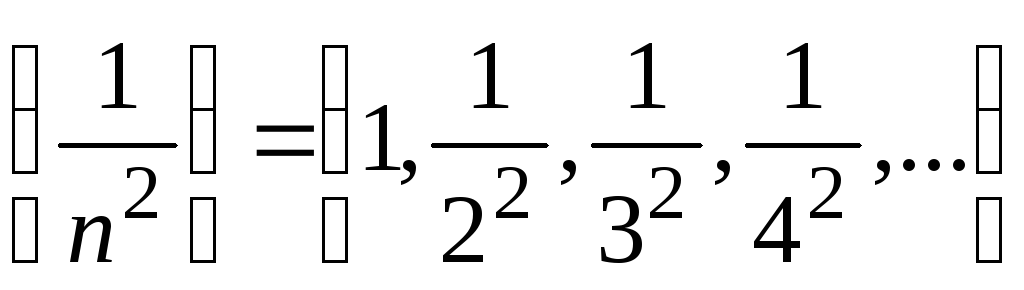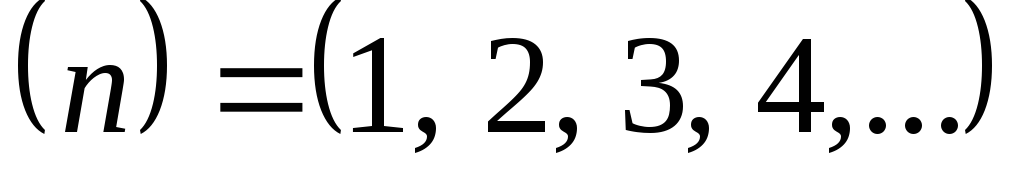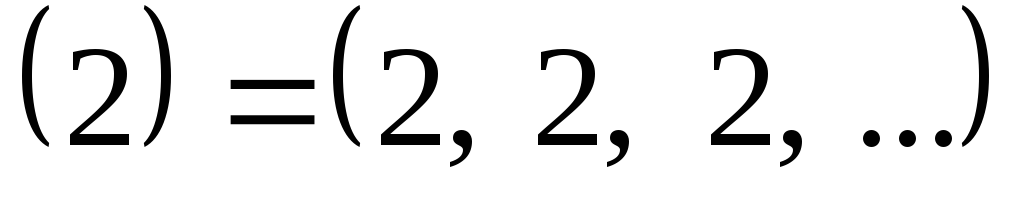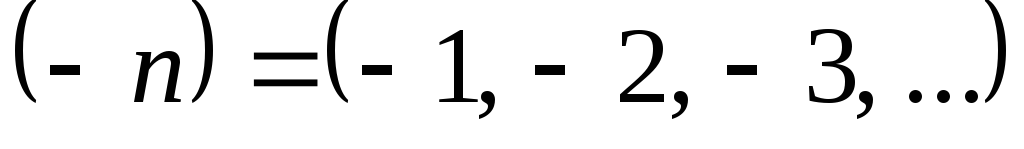Определение 2 Последовательность называется ограниченной снизу (сверху), если и ,

Определение 3 Последовательность называется ограниченной, если она ограничена сверху и снизу.

В приведенных выше примерах:

1. – ограничена, например, число для ;

2. ограничена снизу, например, (или любое число ;

3. – ограничена, например,

4. – ограничена, например, ;

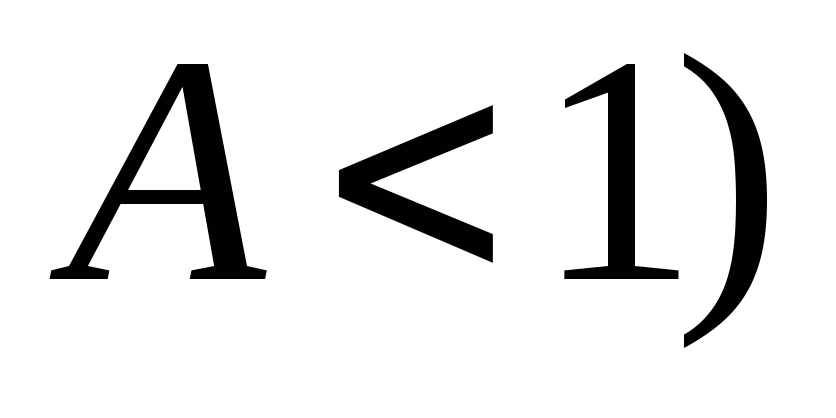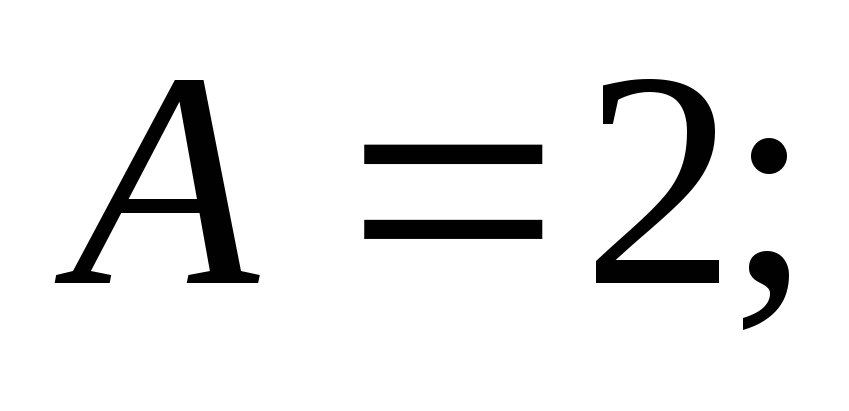
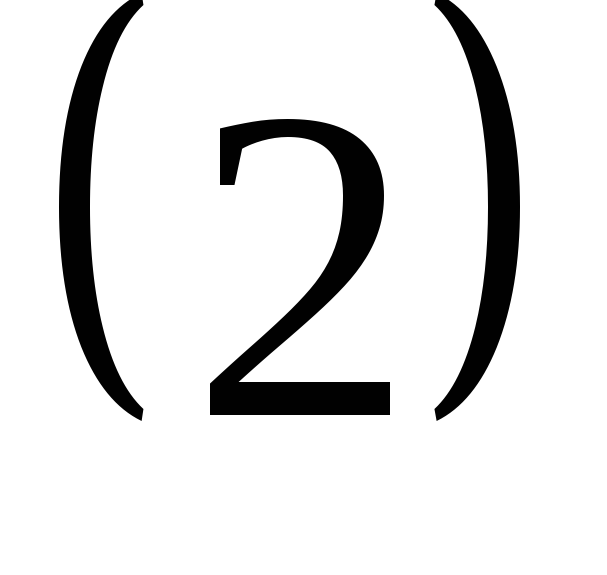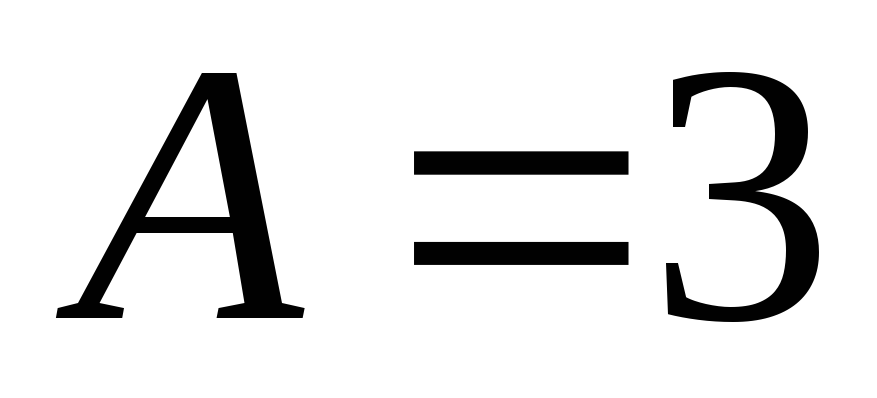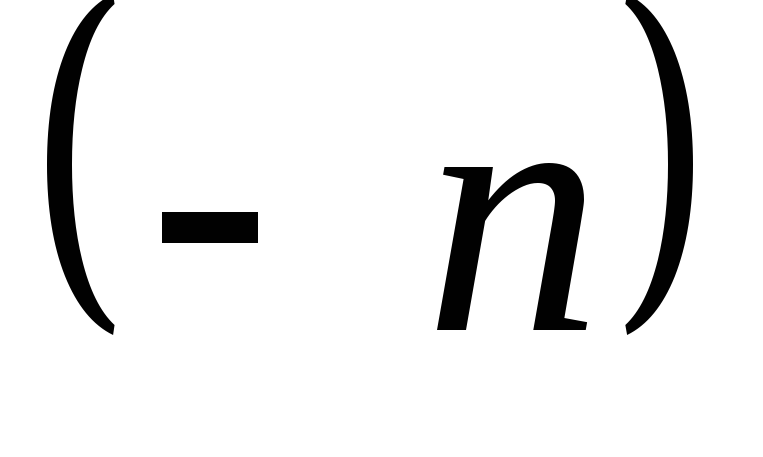5. – ограничена сверху, например, .

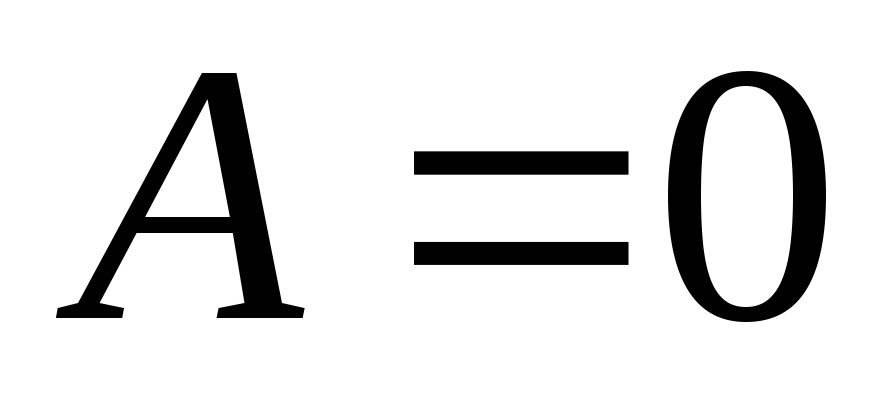Определение 4 – окрестностью («эпсилон»-окрестностью) точки а называют любой интервал , :

Если убрать точку а, то такая окрестность будет называться проколотой.

Определение 5 Число а называется пределом числовой последовательности при , если для любого положительного сколько угодно малого числа существует номер , такой, что для всех выполняется неравенство

. (2)

Предел числовой последовательности обозначается .

Используя логические символы, данное определение можно записать в виде:

 .

Неравенство (2) равносильно неравенству

т. е., с геометрической точки зрения, число а будет пределом числовой последовательности , если в любой -окрестности точки а содержатся все члены последовательности, за исключением конечного их числа (ровно элементов находится за пределами данной -окрестности):

Определение 6 Последовательность, имеющая конечный предел, называется сходящейся. Последовательность, не имеющая предела, называется расходящейся. Если х_n стремится (при n  ) к –  или + , то говорят, что последовательность сходится к бесконечности, т.е.

.

Пример. Доказать, что число является пределом последовательности . Найти, сколько элементов данной последовательности не попало в -окрестность числа , если .

Решение. Из неравенства (2) следует

Таким образом, (целая часть числа, так как – это номер элемента,  достаточно мало). Следовательно, при , т. е. число является пределом данной числовой последовательности.

Пусть Следовательно, ровно 1999 элементов находится за пределами интервала =:

,

.