МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Частный институт управления и предпринимательства
Н.Н.Рачковский
ЭКОНОМИКО-МАТЕМЕТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ
Сборник задач по линейному программированию
Учебно-методическое пособие
Минск 2005
УДК 51
ББК
Автор
Н.Н.Рачковский, доцент кафедры высшей математики и статистики,
кандидат физико-математических наук, доцент
Рецензенты:
В.А.Янцевич, доцент кафедры алгебры и геометрии Белорусского государственного педагогического университета имени Максима Танка, кандидат физико-математических наук, доцент;
В.К.Пономаренко, доцент кафедры прикладной математики и информатики Белорусского государственного педагогического университета имени Максима Танка, кандидат физико-математических наук, доцент.
Обсуждено и одобрено на заседании
кафедры высшей математики и статистики,
протокол №5 от 23 ноября 2005 г.
Рачковский Н.Н.
Экономико-математические методы и модели. Сборник задач по линейному программированию: Учеб.-метод. пособие / Н.Н.Рачковский. – Мн.: Частн. Ин-т упр. и предпр., 2005. – 41 с.
ISBN
Пособие включает типовые задачи по линейному программированию.
Предназначено для студентов дневной и заочной форм обучения Частного института управления и предпринимательства.
УДК 51
ББК
ISBN © Н.Н.Рачковский. 2005
© Частный институт управления и предпринимательства. 2005
Графический метод решения задач линейного программирования
Графический метод особенно удобен при решении задач линейного программирования, содержащих только две переменные, т.е. задач вида
Здесь символ
означает, что рассматривается как задача
максимизации, так и задача минимизации,
а символ
означает, что знак неравенства в
ограничениях задачи может быть любой.
Заметим также, что мы не рассматриваем
здесь задачи, в которых присутствуют
ограничения-равенства, с одной стороны,
в силу их достаточной тривиальности,
а с другой стороны, из-за того, что
равенства можно рассматривать как
систему двух нестрогих неравенств,
отличающихся друг от друга только знаком
неравенства (например, равенство
равносильно системе неравенств
).
Графическое решение задачи линейного программирования осуществляется в четыре этапа. На первом этапе па координатной плоскости строится множество допустимых решений данной задачи, т.е. множество решений системы неравенств из условия задачи. Для этого строится множество решений каждого неравенства этой системы, а затем рассматривается пересечение всех этих множеств.
На втором этапе
на той же координатной плоскости
изображается вектор
,
указывающий направление наискорейшего
роста целевой функции
данной задачи. Напомним, что для
построения вектора
нужно построить точку с этими координатами
,
соединить ее с началом координат отрезком
и взять направление от начала координат.
На третьем этапе
строится линия уровня
целевой функции, т.е. прямая, задаваемая
уравнением
.
При этом бывает полезным учитывать, что
эта прямая перпендикулярна вектору
и проходит через начало координат.
На четвертом этапе
через каждую точку множества допустимых
решений мысленно проводится прямая,
параллельная линии уровня целевой
функции
(заметим, что таких прямых, как правило,
бесконечно много, так как обычно множество
допустимых решений содержит бесконечно
много точек; именно поэтому и следует
эти прямые проводить мысленно). Если
решается задача максимизации целевой
функции, то среди всех этих мысленно
проведенных прямых выбирается крайняя
в направлении вектора
(например, если вектор
направлен вверх, то выбирается самая
верхняя прямая, если этот вектор направлен
вправо, то – самая правая и т. д.). Если
же решается задача минимизации целевой
функции, то среди всех этих мысленно
проведенных прямых выбирается крайняя
в направлении, противоположном вектору
(например, если вектор
направлен вверх, то выбирается самая
нижняя прямая, если этот вектор направлен
вправо, то – самая левая и т. д.). Координаты
всех точек пересечения множества
допустимых решений с этой крайней прямой
являются решениями рассматриваемой
задачи.
Может оказаться, что такой крайней прямой нет из-за неограниченности множества допустимых решений; в этом случае данная задача не имеет оптимального решения из-за неограниченности целевой функции на множестве допустимых решений. Может также случиться, что множество допустимых решений пусто, т.е. система неравенств из условия задачи несовместна; понятно, что и в этом случае задача не имеет оптимального решения.
Замечание. Если множество допустимых решений ограничено т.е. целиком содержится в некотором круге (это означает, что множество допустимых решений является либо точкой, либо отрезком, либо выпуклым многоугольником), то на четвертом этапе решения задачи достаточно провести прямые, параллельные линии уровня целевой функции только через крайние (угловые) точки множества допустимых решений, и только среди них выбирать крайние.
Пример 1. Решить графически следующую задачу линейного программирования:
Решение.
1. Изобразим множество допустимых решений данной задачи. Для этого изобразим множество решений каждого неравенства этой задачи.
Начнем с первого
неравенства:
.
Заменим знак неравенства знаком
равенства:
.
Получили уравнение некоторой прямой;
построим эту прямую по двум точкам,
например, по точкам пересечения ее с
осями координат. Взяв
,
получим
,
а взяв
,
получим
.
Таким образом, получили две точки данной
прямой: (0;1) и (–5;0). Изобразим эти точки
и проведем через них прямую:
Построенная прямая
является решением уравнения
.
Эта прямая делит плоскость на две
полуплоскости. Решением данного
неравенства
является одна из этих полуплоскостей;
чтобы указать, какая именно, возьмем
любую точку, не лежащую на этой
прямой, и подставим ее координаты в
данное неравенство. Если в результате
такой подстановки получится верное
числовое неравенство, то заштрихуем
полуплоскость, содержащую эту взятую
нами точку. Если же в результате указанной
подстановки получится неверное
числовое неравенство, то заштрихуем
полуплоскость, не содержащую эту
взятую нами точку. При этом бывает удобно
брать точку на какой-либо координатной
оси. В нашем случае, например, точка
О(0;0) не лежит на построенной нами
прямой; подставим ее координаты в
рассматриваемое неравенство и получим
числовое неравенство
или
.
Это числовое неравенство не является
верным, поэтому заштрихуем полуплоскость,
не содержащую точку О(0;0); поскольку
эта точка лежит ниже построенной нами
прямой, то заштрихуем полуплоскость,
лежащую выше этой прямой.
Аналогично решается
второе неравенство
.
Заменим знак неравенства знаком равенства
и получим уравнение прямой
.
Построим эту прямую по двум точкам: если
,
то
,
а если
,
то
.
Таким образом, получили две точки
пересечения данной прямой с осями
координат: (0;7) и (4;0). На той же координатной
плоскости изобразим эти точки и проведем
через них прямую.
Чтобы указать
полуплоскость, являющуюся решением
данного неравенства
,
возьмем точку О(0;0), не лежащую на
построенной прямой, и подставим ее
координаты в данное неравенство:
,
т.е.
.
Получилось верное числовое неравенство,
поэтому заштрихуем полуплоскость,
лежащую ниже построенной прямой, так
как именно нижняя полуплоскость содержит
точку О(0;0).
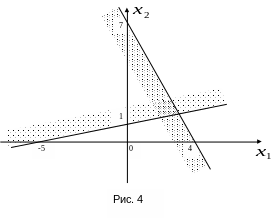
Рассмотрим теперь
третье неравенство
.
Заменим знак неравенства знаком равенства
и получим уравнение прямой
.
Построим эту прямую по двум точкам: если
,
то
,
а если
,
то
.
Таким образом, получили две точки данной
прямой: (0;0) и (2;7). На той же координатной
плоскости изобразим эти точки и проведем
через них прямую.
Чтобы указать
полуплоскость, являющуюся решением
данного неравенства
,
возьмем точку (1;0), не лежащую на построенной
прямой, и подставим ее координаты в
данное неравенство:
,
т.е.
.
Получилось неверное числовое неравенство,
поэтому заштрихуем полуплоскость,
лежащую выше построенной прямой, так
как именно верхняя полуплоскость не
содержит точку (1;0).
Наконец, рассмотрим
последнее неравенство
.
Решением этого неравенства является
полуплоскость, лежащая справа от
вертикальной координатной оси. Заштрихуем
ее и выделим область координатной
плоскости, содержащую все четыре
нанесенные нами штриховки. Нетрудно
видеть, что этой областью является
выпуклый четырехугольник ABCD.
2. Изобразим теперь
вектор
,
указывающий направление наискорейшего
роста целевой функции
данной задачи (координаты этого вектора
равны коэффициентам при переменных в
целевой функции).
3. Построим прямую
,
т.е.
– линию уровня целевой функции. Для
этого также найдем две точки этой прямой:
если
,
то
,
а если
,
то
.
Таким образом, линия уровня целевой
функции
проходит через точки (0;0) и (3;2). Заметим,
что эту прямую можно построить, не находя
точки, через которые она проходит;
достаточно вспомнить, что она
перпендикулярна вектору
и проходит через начало координат, но
при этом нужно учитывать, что ее
перпендикулярность вектору
имеет место лишь в случае, когда на
координатных осях выбрана одна и та же
единица измерения.
4. Поскольку
построенное на первом этапе множество
допустимых решений данной задачи
ограничено, то через каждую его угловую
точку проведем прямую, параллельную
линии уровня целевой функции
(на
рисунке они проведены пунктиром). Выделим
среди этих прямых крайние; в нашем случае
это прямые, проходящие через точку B
и через точку D. Крайнюю
в направлении вектора
прямую (в нашем случае это пунктирная
прямая, проходящая через точку B)
обозначим через
,
а крайнюю в противоположном направлении
прямую (в нашем случае это пунктирная
прямая, проходящая через точку D)
обозначим через
.
Прямая
пересекает множество допустимых решений
в точке D(0;7), поэтому
решением задачи минимизации целевой
функции на множестве допустимых решений
являются координаты точки D,
т.е. пара чисел (0;7). Прямая
пересекает множество допустимых решений
в точке В, поэтому решением задачи
максимизации целевой функции на множестве
допустимых решений являются координаты
точки В.
Координаты точки В неизвестны. Найдем их, решив систему, составленную из уравнений прямых, ограничивающих множество допустимых решений и проходящих через точку В:
Решением этой
системы является пара чисел
.
Следовательно, эта пара чисел и является
решением задачи максимизации целевой
функции на множестве допустимых решений.
В рассмотренном выше примере множество допустимых решений ограничено, поэтому обе задачи (и минимизации, и максимизации целевой функции на множестве допустимых решений) имеют оптимальное решение. Ниже будет рассмотрен случай, когда из-за того, что множество допустимых решений неограничено, одна из этих задач имеет оптимальное решение, а другая – нет.
Пример 2. Решить графически следующую задачу линейного программирования:
Решение.
1. Изобразим множество допустимых решений данной задачи. Для этого изобразим множество решений каждого неравенства этой задачи. Действуя так же, как в примере 1, получим следующее множество допустимых решений:
2. Изобразим теперь
вектор
(1;5),
указывающий направление наискорейшего
роста целевой функции
данной задачи.
3. Построим линию
уровня целевой функции
,
т.е. прямую
.
4. Заметим, что в данном примере множество допустимых решений неограничено, поэтому мы не можем ограничиться рассмотрением прямых, параллельных линии уровня целевой функции , проходящих только через угловые точки множества допустимых решений. Таким образом, через каждую точку множества допустимых решений мысленно проведем прямую, параллельную линии уровня целевой функции . Вектор направлен вверх, поэтому при решении задачи максимизации целевой функции попытаемся найти среди этих мысленно проведенных прямых самую верхнюю; заметим, что в силу неограниченности множества допустимых решений такой самой верхней прямой нет. Следовательно, данная задача максимизации целевой функции не имеет оптимальных решений из-за того, что целевая функция неограниченно возрастает на множестве допустимых решений.
Для решения задачи минимизации целевой функции попытаемся найти среди мысленно проведенных прямых самую нижнюю; заметим, что такая прямая существует – это прямая, проходящая через точку С. Обозначим эту прямую через . Прямая пересекает множество допустимых решений в единственной точке С; следовательно, оптимальным решением задачи минимизации целевой функции являются координаты точки С. Координаты этой точки неизвестны; чтобы найти их, решим систему, составленную из уравнений прямых, ограничивающих множество допустимых решений и проходящих через точку С:
Решением этой
системы является пара чисел
.
Следовательно, эта пара чисел и является
решением задачи минимизации целевой
функции на множестве допустимых решений.
Рассмотрим теперь случай, когда обе задачи (и минимизации, и максимизации) не имеют оптимальных решений из-за неограниченности целевой функции на множестве допустимых решений.
Пример 3. Решить графически следующую задачу линейного программирования:
Решение.
1. Изобразим множество допустимых решений данной задачи. Для этого изобразим множество решений каждого неравенства этой задачи. Действуя так же, как в предыдущих примерах, получим следующее множество допустимых решений:
2. Изобразим теперь
вектор
(2;–2),
указывающий направление наискорейшего
роста целевой функции
данной задачи.
3. Построим линию
уровня целевой функции
,
т.е. прямую
.
4. Заметим, что и в этом примере множество допустимых решений неограничено, поэтому мы не можем ограничиться рассмотрением прямых, параллельных линии уровня целевой функции , проходящих только через угловые точки множества допустимых решений. Таким образом, через каждую точку множества допустимых решений мысленно проведем прямую, параллельную линии уровня целевой функции . Вектор направлен вниз, поэтому при решении задачи максимизации целевой функции попытаемся найти среди этих мысленно проведенных прямых самую нижнюю; заметим, что такой самой нижней прямой нет. Следовательно, данная задача максимизации целевой функции не имеет оптимальных решений из-за того, что целевая функция неограниченно возрастает на множестве допустимых решений. Заметим также, что нет и самой верхней прямой; следовательно, задача минимизации целевой функции не имеет оптимальных решений из-за того, что целевая функция неограниченно убывает на множестве допустимых решений.
Теперь приведем пример, показывающий, что задача линейного программирования может иметь бесконечное множество оптимальных решений.
Пример 4. Решить графически следующую задачу линейного программирования:
Решение.
1. Изобразим множество допустимых решений данной задачи. Для этого изобразим множество решений каждого неравенства этой задачи. Действуя так же, как в предыдущих примерах, получим следующее множество допустимых решений – четырехугольник ОABC:
2. Изобразим теперь
вектор
(4;6),
указывающий направление наискорейшего
роста целевой функции
данной задачи.
3. Построим линию
уровня целевой функции
,
т.е. прямую
.
Заметим, что линия уровня целевой функции параллельна стороне ВС множества допустимых решений.
4. Поскольку
множество допустимых решений данной
задачи ограничено, то через каждую его
угловую точку проведем прямую, параллельную
линии уровня целевой функции
(на рисунке они проведены пунктиром).
Выделим среди этих прямых крайние; в
нашем случае это прямая, проходящая
через точку А и прямая ВС. Крайнюю
в направлении вектора
прямую (в нашем случае это пунктирная
прямая ВС) обозначим через
,
а крайнюю в противоположном направлении
прямую (в нашем случае это пунктирная
прямая, проходящая через точку А)
обозначим через
.
Прямая
пересекает множество допустимых решений
по отрезку ВС, поэтому решением
задачи максимизации целевой функции
на множестве допустимых решений являются
координаты всех точек отрезка ВС.
Прямая ВС, как видно из наших
построений, задается уравнением
;
поэтому координаты всех точек отрезка
ВС также удовлетворяют этому
уравнению. Осталось только указать
диапазон изменений, например, первой
координаты
для точек этого отрезка. Для этого найдем
первые координаты точек В и С,
решив соответствующие системы линейных
уравнений. Решая систему
,
найдем координаты
точки
.
Решая систему
,
найдем координаты
точки
.
Таким образом, множество оптимальных
решений задачи максимизации целевой
функции выглядит следующим образом:
.
Прямая
пересекает множество допустимых решений
в точке А, поэтому решением задачи
минимизации целевой функции на множестве
допустимых решений являются координаты
точки А, т.е. пара чисел
.
Выше мы рассматривали случаи, когда множество допустимых решений имеет непустую внутренность, т.е. является либо выпуклым многоугольником, либо неограниченной многогранной областью. Однако, достаточно часто встречаются случаи, когда множество допустимых решений в этом смысле вырождено, а именно является отрезком прямой, лучом, прямой или даже пустым множеством. Итак, сначала рассмотрим случай, когда множество допустимых решений является отрезком прямой. В этом случае обе задачи (и минимизации, и максимизации целевой функции на множестве допустимых решений) имеют оптимальное решение. Следующий пример показывает, что эти оптимальные решения могут быть различными для каждой из обеих указанных задач.
Пример 5. Решить графически следующую задачу линейного программирования:
Решение.
1. Изобразим множество допустимых решений данной задачи. Для этого изобразим множество решений каждого неравенства этой задачи. Действуя так же, как в предыдущих примерах, получим следующее множество допустимых решений – отрезок АВ.
2. Изобразим теперь
вектор
(4;3),
указывающий направление наискорейшего
роста целевой функции
данной задачи.
3. Построим линию
уровня целевой функции
,
т.е. прямую
.
4. Поскольку множество допустимых решений данной задачи – отрезок АВ – ограничено, то через его крайние точки А и В проведем прямые, параллельные линии уровня целевой функции (на рисунке они проведены пунктиром). Из них крайнюю в направлении вектора (в нашем случае это пунктирная прямая, проходящая через точку А) обозначим через , а крайнюю в противоположном направлении (в нашем случае это пунктирная прямая, проходящая через точку В) обозначим через .
Прямая пересекает множество допустимых решений в точке А, поэтому решением задачи максимизации целевой функции на множестве допустимых решений являются координаты точки А, т.е. пара чисел (0;6).
Прямая пересекает множество допустимых решений в единственной точке В; следовательно, оптимальным решением задачи минимизации целевой функции являются координаты точки В. Координаты этой точки неизвестны; чтобы найти их, решим систему, составленную из уравнений прямых, ограничивающих множество допустимых решений и проходящих через точку В:
Решением этой
системы является пара чисел
.
Следовательно, эта пара чисел и является
решением задачи минимизации целевой
функции на множестве допустимых решений.
Пример 6. Решить графически следующую задачу линейного программирования:
Решение.
1. Изобразим множество допустимых решений данной задачи. Для этого изобразим множество решений каждого неравенства этой задачи. Действуя так же, как в предыдущих примерах, получим следующее множество допустимых решений – отрезок АВ.
2. Изобразим теперь
вектор
(3;–3),
указывающий направление наискорейшего
роста целевой функции
данной задачи.
3. Построим линию
уровня целевой функции
,
т.е. прямую
.
4. Заметим, что
линия уровня целевой функции
параллельна отрезку АВ – множеству
допустимых решений данной задачи,
поэтому обе прямые
и
совпадают с прямой АВ. Следовательно,
координаты всех точек отрезка АВ
являются оптимальными решениями и
задачи максимизации, и задачи минимизации
целевой функции на множестве допустимых
решений. Прямая АВ, как видно из
наших построений, задается уравнением
;
поэтому координаты всех точек отрезка
АВ также удовлетворяют этому
уравнению. Осталось только указать
диапазон изменений, например, первой
координаты
для точек этого отрезка. Для этого найдем
первые координаты точек А и В,
решив соответствующие системы линейных
уравнений. Решая систему
,
найдем координаты точки А(1,5;–0,5). Решая систему
,
найдем координаты
точки В(3,2;1,2). Таким образом, множество
оптимальных решений обеих задач и
максимизации, и минимизации целевой
функции выглядит следующим образом:
.
Теперь мы рассмотрим случай, когда множество допустимых решений является лучом. В этом случае либо одна из задач (то ли минимизации, то ли максимизации целевой функции на множестве допустимых решений) имеет оптимальное решение, а другая – нет (из-за неограниченности целевой функции на множестве допустимых решений), либо обе эти задачи имеют одно и то же бесконечное множество оптимальных решений, совпадающее с этим лучом.
Пример 7. Решить графически следующую задачу линейного программирования:
Решение.
1. Изобразим множество допустимых решений данной задачи. Для этого изобразим множество решений каждого неравенства этой задачи. Действуя так же, как в предыдущих примерах, получим следующее множество допустимых решений – луч АВ.
2. Изобразим теперь
вектор
(5;–2),
указывающий направление наискорейшего
роста целевой функции
данной задачи.
3
.
Построим линию уровня целевой функции
,
т.е. прямую
.
4. Заметим, что в
этом примере множество допустимых
решений – луч АВ – неограничено,
поэтому через каждую точку множества
допустимых решений мысленно проведем
прямую, параллельную линии уровня
целевой функции
.
Вектор
направлен вправо, поэтому при решении
задачи максимизации целевой функции
попытаемся найти среди этих мысленно
проведенных прямых самую правую; заметим,
что такой самой правой прямой нет.
Следовательно, данная задача максимизации
целевой функции не имеет оптимальных
решений из-за того, что целевая функция
неограниченно возрастает на множестве
допустимых решений. Для определения
оптимального решения задачи минимизации
целевой функции среди указанных выше
мысленно проведенных прямых найдем
самую левую; очевидно, это прямая,
проходящая через точку А (на рисунке
она проведена пунктиром и обозначена
через
).
Следовательно, оптимальным решением
задачи минимизации целевой функции
являются координаты точки А. Найдем
эти координаты. Для этого решим систему,
составленную из уравнений прямых,
проходящих через точку А:
.
Решением этой системы является пара
чисел (1,6;2,8). Таким образом, эта пара
чисел и является решением задачи
минимизации целевой функции на множестве
допустимых решений.
Пример 8. Решить графически следующую задачу линейного программирования:
Решение.
1. Изобразим множество допустимых решений данной задачи. Для этого изобразим множество решений каждого неравенства этой задачи. Действуя так же, как в предыдущих примерах, получим следующее множество допустимых решений – луч АВ.
2. Изобразим теперь
вектор
(2;–4),
указывающий направление наискорейшего
роста целевой функции
данной задачи.
3. Построим линию
уровня целевой функции
,
т.е. прямую
.
4. Заметим, что
линия уровня целевой функции
параллельна лучу АВ – множеству
допустимых решений данной задачи,
поэтому обе прямые
и
совпадают с прямой АВ. Следовательно,
координаты всех точек луча АВ
являются оптимальными решениями и
задачи максимизации, и задачи минимизации
целевой функции на множестве допустимых
решений. Прямая АВ, как видно из
наших построений, задается уравнением
;
поэтому координаты всех точек луча АВ
также удовлетворяют этому уравнению.
Нетрудно видеть, что для первой координаты
каждой точки луча АВ справедливо
неравенство
.
Таким образом, множество оптимальных
решений обеих задач и максимизации, и
минимизации целевой функции выглядит
следующим образом:
.
Рассмотрим теперь случай, когда множеством допустимых решений является прямая. Как мы увидим ниже, в этом случае В этом случае либо обе задачи (и минимизации, и максимизации целевой функции на множестве допустимых решений) не имеют оптимального решения из-за неограниченности целевой функции на множестве допустимых решений, либо обе эти задачи имеют одно и то же бесконечное множество оптимальных решений, совпадающее с этой прямой.
Пример 9. Решить графически следующую задачу линейного программирования:
Решение.
1. Изобразим множество допустимых решений данной задачи. Для этого изобразим множество решений каждого неравенства этой задачи. Действуя так же, как в предыдущих примерах, получим следующее множество допустимых решений – прямая АВ.
2. Изобразим теперь
вектор
(4;1),
указывающий направление наискорейшего
роста целевой функции
данной задачи.
3. Построим линию
уровня целевой функции
,
т.е. прямую
.
4. Заметим, что в этом примере множество допустимых решений – прямая АВ – неограничено, поэтому через каждую точку множества допустимых решений мысленно проведем прямую, параллельную линии уровня целевой функции . Вектор направлен вправо, поэтому при решении задачи максимизации целевой функции попытаемся найти среди этих мысленно проведенных прямых самую правую; заметим, что такой самой правой прямой нет. Следовательно, данная задача максимизации целевой функции не имеет оптимальных решений из-за того, что целевая функция неограниченно возрастает на множестве допустимых решений. Заметим также, что нет и самой левой прямой; следовательно, задача минимизации целевой функции не имеет оптимальных решений из-за того, что целевая функция неограниченно убывает на множестве допустимых решений.
Пример 10. Решить графически следующую задачу линейного программирования:
Решение.
1. Изобразим множество допустимых решений данной задачи. Для этого изобразим множество решений каждого неравенства этой задачи. Действуя так же, как в предыдущих примерах, получим следующее множество допустимых решений – прямая АВ.
2. Изобразим теперь
вектор
(1;2),
указывающий направление наискорейшего
роста целевой функции
данной задачи.
3. Построим линию
уровня целевой функции
,
т.е. прямую
.
4. Заметим, что
линия уровня целевой функции
параллельна прямой АВ – множеству
допустимых решений данной задачи,
поэтому обе прямые
и
совпадают с прямой АВ. Следовательно,
координаты всех точек прямой АВ
являются оптимальными решениями и
задачи максимизации, и задачи минимизации
целевой функции на множестве допустимых
решений. Прямая АВ, как видно из
наших построений, задается уравнением
;
поэтому множество оптимальных решений
обеих задач и максимизации, и минимизации
целевой функции выглядит следующим
образом:
.
Следующий пример показывает, что множество допустимых решений может состоять из одной точки. Понятно, что в таком случае координаты этой точки при любой целевой функции являются оптимальным решением как задачи максимизации, так и задачи минимизации целевой функции на множестве допустимых решений; поэтому необходимость в проведении последних трех этапов решения задачи исчезает.
Пример 11. Решить графически следующую задачу линейного программирования:
Решение.
1. Изобразим множество допустимых решений данной задачи. Для этого изобразим множество решений каждого неравенства этой задачи. Действуя так же, как в предыдущих примерах, получим следующее множество допустимых решений – точку А.
Следовательно,
координаты точки А являются
оптимальным решением и задачи максимизации,
и задачи минимизации целевой функции
на множестве допустимых решений. Найдем
эти координаты; для этого решим систему
,
составленную из уравнений прямых,
проходящих через точку А (поскольку
все три прямые проходят через точку А,
то мы выбрали из них те две, которые
задаются более простыми уравнениями).
Решением этой системы является пара
чисел (2;1). Таким образом эта пара чисел
является оптимальным решением и задачи
максимизации, и задачи минимизации
целевой функции.
Наконец, заключительный пример показывает, что множество допустимых решений может быть пустым. Очевидно, в этом случае и задача максимизации, и задача минимизации целевой функции не имеет оптимальных решений.
Пример 12. Решить графически следующую задачу линейного программирования:
Решение.
1. Изобразим множество допустимых решений данной задачи. Для этого изобразим множество решений каждого неравенства этой задачи. Действуя так же, как в предыдущих примерах, получим пустое множество допустимых решений.
Следовательно, и задача максимизации, и задача минимизации целевой функции не имеет оптимальных решений.