
- •Частный институт управления и предпринимательства
- •Определенный интеграл Минск 2007
- •М 54 Высшая математика. Определенный интеграл: учеб.-метод. Посо-бие / в. М. Метельский. – Минск: Частн. Ин-т упр. И предпр., 2007. – 29 с.
- •Ключевые понятия
- •Понятие определенного интеграла
- •Геометрический смысл определенного интеграла
- •3. Основные свойства определенного интеграла
- •4. Формула Ньютона–Лейбница
- •5. Замена переменной в определенном интеграле
- •Интегрирование по частям
- •Доказательство
- •Задачи и упражнения Определенный интеграл
- •Объем тела вращения
- •Длина дуги плоской кривой
- •Несобственные интегралы с бесконечными пределами интегрирования
- •Несобственные интегралы от неограниченных функций
- •Задачи и упражнения Применение определенных интегралов. Несобственные интегралы
- •Литература
- •Ответы к задачам и упражнениям Определенный интеграл
- •Применение определенных интегралов. Несобственные интегралы
- •Содержание
- •Метельский Василий Михайлович высшая математика Определенный интеграл
- •220086, Г. Минск, ул. Славинского 1, корп. 3.
Частный институт управления и предпринимательства
В. М. Метельский
ВЫСШАЯ МАТЕМАТИКА
Определенный интеграл Минск 2007
Частный институт управления и предпринимательства
В. М. Метельский
ВЫСШАЯ МАТЕМАТИКА
Определенный интеграл
Учебно-методическое пособие

Минск 2007
УДК 51(075.8):33
ББК 22.1я73
М 54
Рекомендовано к изданию редакционно-издательским советом Частного института управления и предпринимательства
А в т о р
доцент кафедры высшей математики и статистики
Частного института управления и предпринимательства
кандидат физико-математических наук В. М. Метельский
Р е ц е н з е н т ы:
профессор кафедры высшей математики Белорусского государственного экономического университета доктор физико-математических наук, профессор Н. С. Коваленко;
доцент кафедры высшей математики Белорусского национального технического университета кандидат физико-математических наук, доцент Т. И. Чепелева
Рассмотрено и одобрено на заседании кафедры высшей математики и статистики,
протокол № 10 от 11.05.2007 г.
Метельский, В. М.
М 54 Высшая математика. Определенный интеграл: учеб.-метод. Посо-бие / в. М. Метельский. – Минск: Частн. Ин-т упр. И предпр., 2007. – 29 с.
Пособие подготовлено в соответствии с учебной программой ЧИУиП по дисциплине «Высшая математика», стандартом и типовой программой Министерства образования Республики Беларусь. Оно включает лекции, задачи, упражнения и индивидуальные задания по теме «Определенный интеграл».
Для студентов дневной и заочной форм обучения Частного института управления и предпринимательства.
УДК 51(075.8):33
Б БК
22.1я73
БК
22.1я73
Метельский В. М., 2007
Частный институт управления и предпринимательства, 2007
Лекция 1. оПРЕДЕЛЕННЫЙ иНТЕГРАЛ
План
-
Понятие определенного интеграла.
-
Геометрический смысл определенного интеграла.
-
Основные свойства определенного интеграла.
-
Формула Ньютона–Лейбница.
-
Замена переменной в определенном интеграле.
6. Интегрирование по частям.
Ключевые понятия
Интегральная сумма. Определенный интеграл. Пределы интегрирования. Интегрируемая функция. Криволинейная трапеция. Формула Ньютона–Лейбница. Теорема о среднем.
-
Понятие определенного интеграла
Пусть функция
![]() определена на отрезке
определена на отрезке
![]() ,
,
![]() .
Выполним следующие операции:
.
Выполним следующие операции:
-
разобьем отрезок
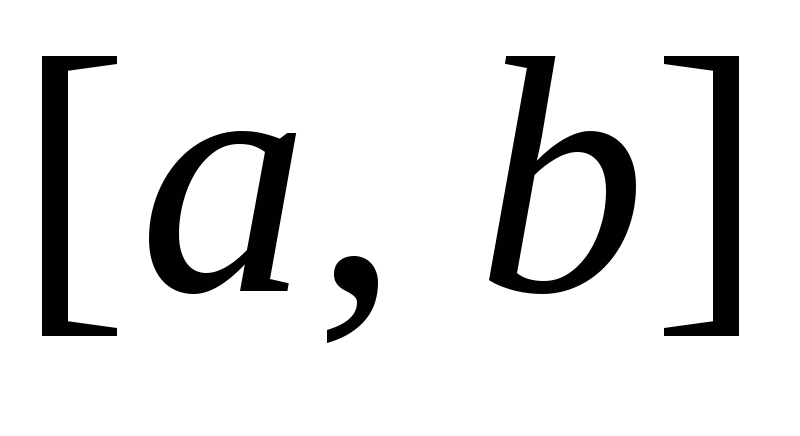 точками
точками
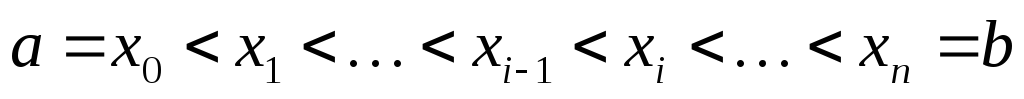 на n
частичных отрезков
на n
частичных отрезков
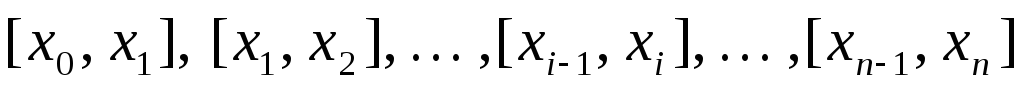 ;
; -
в каждом из частичных отрезков
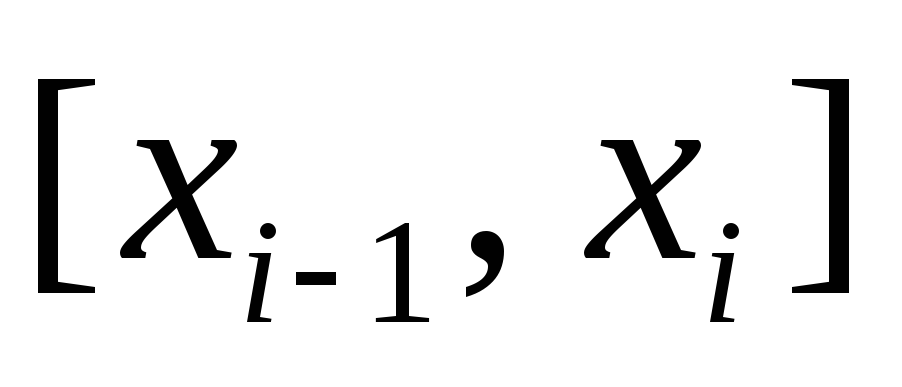 ,
,
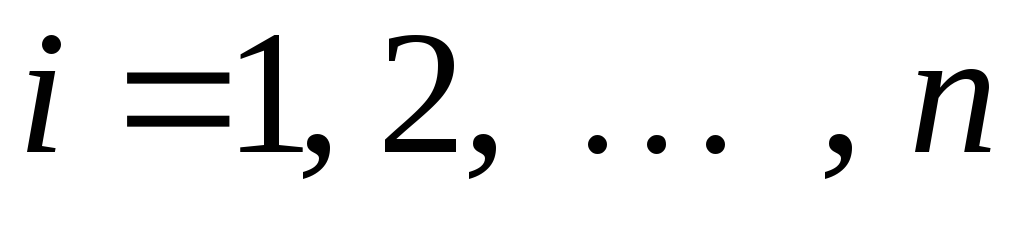 выберем произвольную точку
выберем произвольную точку
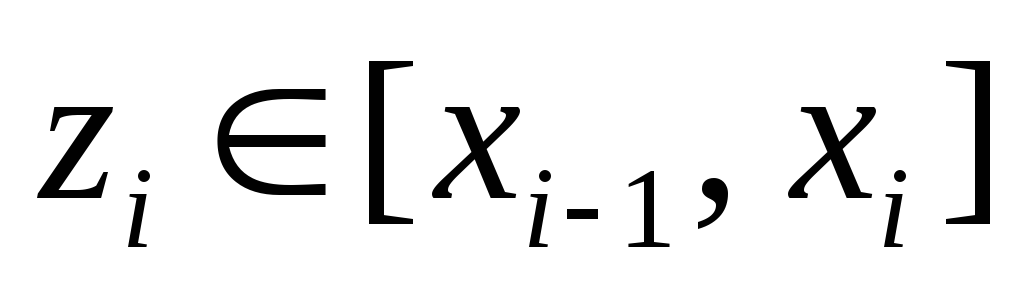 и вычислим значение функции в этой
точке:
и вычислим значение функции в этой
точке:
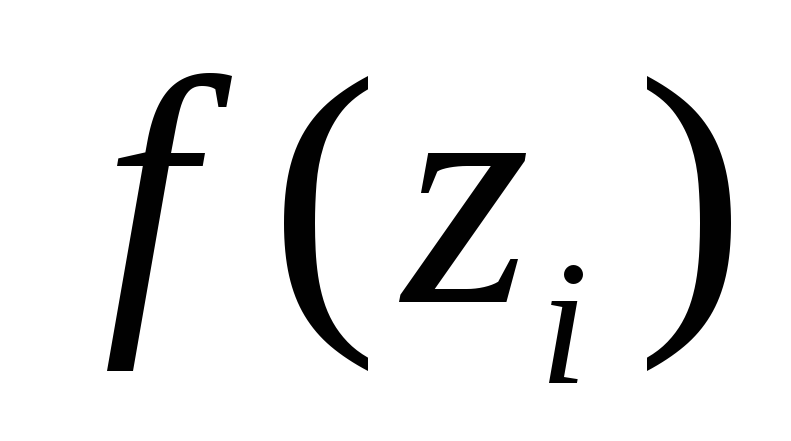 ;
; -
найдем произведения
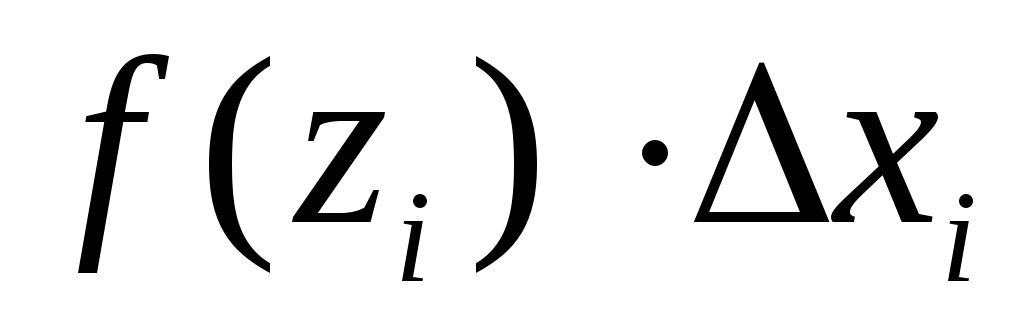 ,
где
,
где
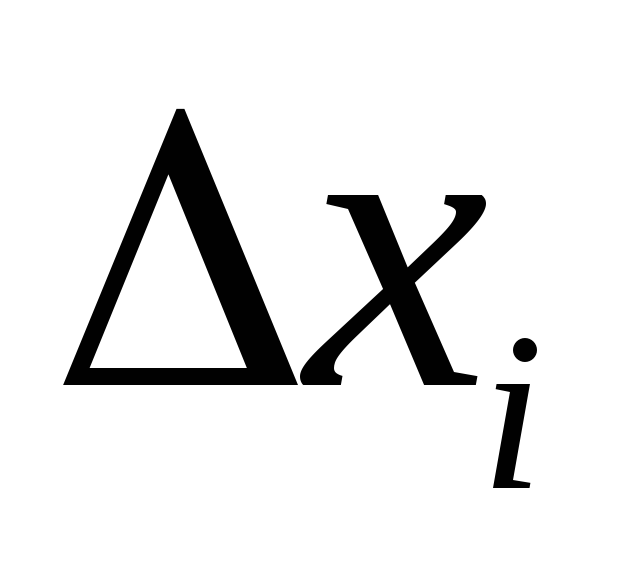 – длина частичного отрезка
– длина частичного отрезка
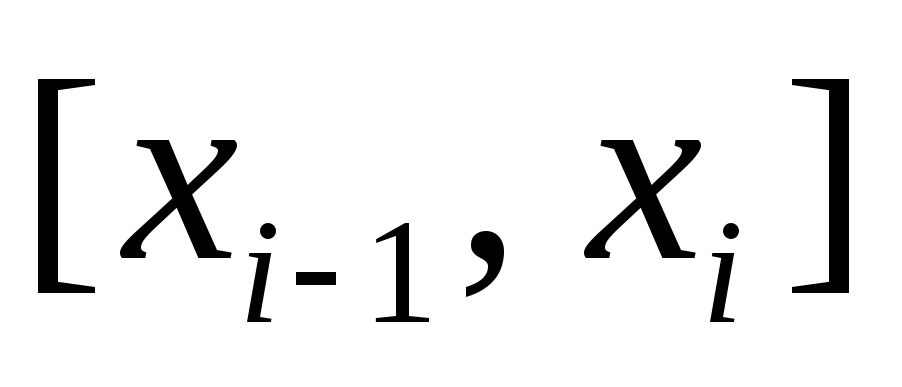 ,
,
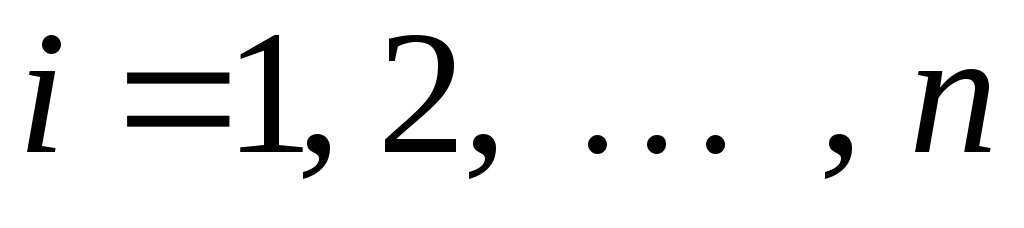 ;
; -
составим сумму
![]() ,
(1)
,
(1)
которая называется
интегральной
суммой функции y
= f(x)
на отрезке
[а,
b].
С геометрической точки зрения интегральная
сумма
![]() представляет собой сумму площадей
прямоугольников, основаниями которых
являются частичные отрезки
представляет собой сумму площадей
прямоугольников, основаниями которых
являются частичные отрезки
![]() ,
а высоты равны
,
а высоты равны
![]() соответственно (рис. 1). Обозначим через
соответственно (рис. 1). Обозначим через
![]() длину наибольшего частичного отрезка
длину наибольшего частичного отрезка
![]() ;
;
-
найдем предел интегральной суммы, когда
 .
.
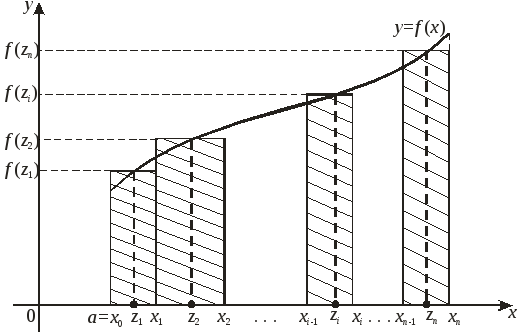
Рис. 1
Определение.
Если существует
конечный предел интегральной суммы (1)
и он не зависит ни от способа разбиения
отрезка
![]() на частичные отрезки, ни от выбора точек
на частичные отрезки, ни от выбора точек
![]() в них, то этот предел называется
определенным интегралом от функции
в них, то этот предел называется
определенным интегралом от функции
![]() на отрезке
на отрезке
![]() и обозначается
и обозначается
![]() .
.
Таким образом,
![]() .
.
В этом случае
функция
![]() называется интегрируемой на
называется интегрируемой на
![]() .
Числа а и
b
называются соответственно нижним и
верхним пределами интегрирования,
.
Числа а и
b
называются соответственно нижним и
верхним пределами интегрирования,
![]() – подынтегральной функцией,
– подынтегральной функцией,
![]() – подынтег-ральным выражением,
– подынтег-ральным выражением,
![]() – переменной интегрирования; отрезок
– переменной интегрирования; отрезок
![]() называется
промежутком интегрирования.
называется
промежутком интегрирования.
Теорема
1. Если
функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() ,
то она интегрируема на этом отрезке.
,
то она интегрируема на этом отрезке.
