
- •Частный институт управления и предпринимательства
- •Определенный интеграл Минск 2007
- •М 54 Высшая математика. Определенный интеграл: учеб.-метод. Посо-бие / в. М. Метельский. – Минск: Частн. Ин-т упр. И предпр., 2007. – 29 с.
- •Ключевые понятия
- •Понятие определенного интеграла
- •Геометрический смысл определенного интеграла
- •3. Основные свойства определенного интеграла
- •4. Формула Ньютона–Лейбница
- •5. Замена переменной в определенном интеграле
- •Интегрирование по частям
- •Доказательство
- •Задачи и упражнения Определенный интеграл
- •Объем тела вращения
- •Длина дуги плоской кривой
- •Несобственные интегралы с бесконечными пределами интегрирования
- •Несобственные интегралы от неограниченных функций
- •Задачи и упражнения Применение определенных интегралов. Несобственные интегралы
- •Литература
- •Ответы к задачам и упражнениям Определенный интеграл
- •Применение определенных интегралов. Несобственные интегралы
- •Содержание
- •Метельский Василий Михайлович высшая математика Определенный интеграл
- •220086, Г. Минск, ул. Славинского 1, корп. 3.
-
Геометрический смысл определенного интеграла
Пусть на отрезке
![]() задана
непрерывная неотрицательная функция
задана
непрерывная неотрицательная функция
![]() .
Криволинейной
трапецией называется фигура, ограниченная
сверху графиком функции y
= f(x),
снизу – осью Ох, слева и справа – прямыми
x
= a
и x
= b
(рис. 2).
.
Криволинейной
трапецией называется фигура, ограниченная
сверху графиком функции y
= f(x),
снизу – осью Ох, слева и справа – прямыми
x
= a
и x
= b
(рис. 2).

Рис. 2
Определенный
интеграл
![]() от неотрицательной функции
от неотрицательной функции
![]() с геометрической точки зрения численно
равен площади криволинейной трапеции,
ограниченной сверху графиком функции
с геометрической точки зрения численно
равен площади криволинейной трапеции,
ограниченной сверху графиком функции
![]() ,
слева и справа – отрезками прямых
,
слева и справа – отрезками прямых
![]() и
и
![]() ,
снизу – отрезком
,
снизу – отрезком
![]() оси Ох.
оси Ох.
3. Основные свойства определенного интеграла
-
Значение определенного интеграла не зависит от обозначения переменной интегрирования:
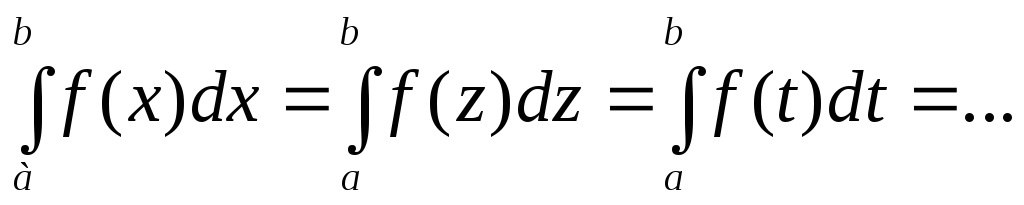 .
.
2.
Определенный
интеграл с одинаковыми пределами
интегрирования равен нулю:
![]()
-
Если
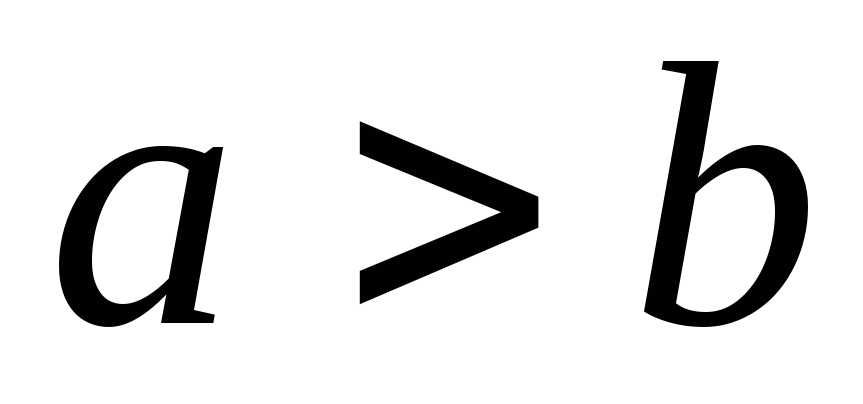 ,
то, по определению, полагаем
,
то, по определению, полагаем
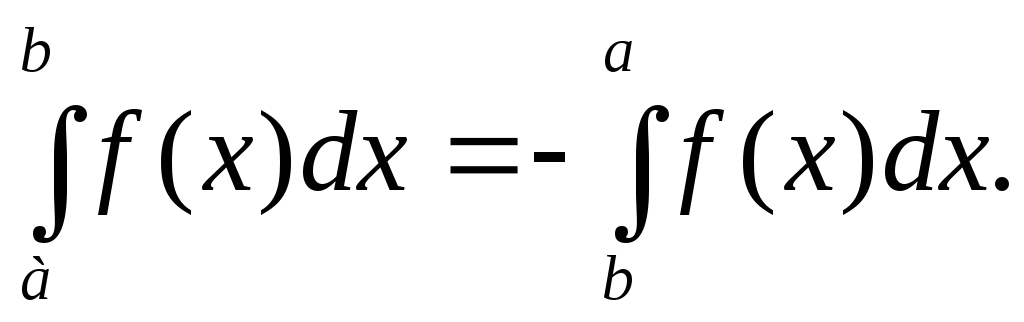
-
Постоянный множитель можно выносить за знак определенного интеграла:
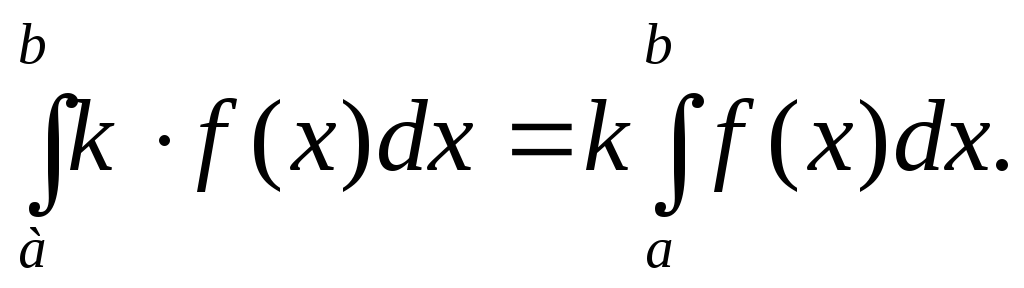
-
Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме определенных интегралов от этих функций:
![]() .
.
-
Если функция
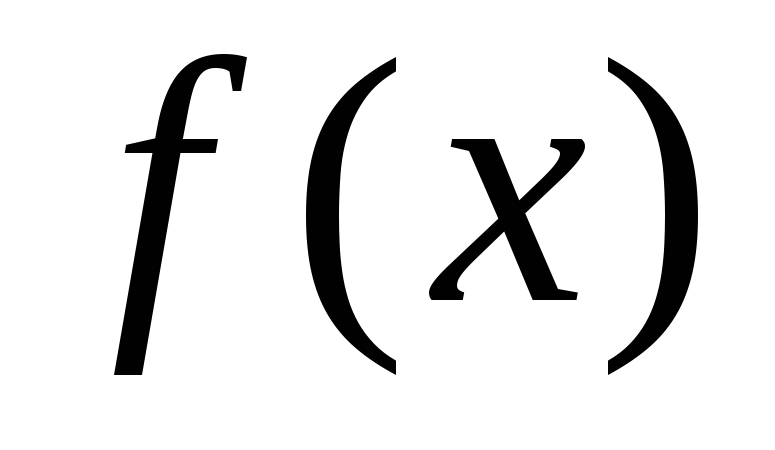 интегрируема
на
интегрируема
на
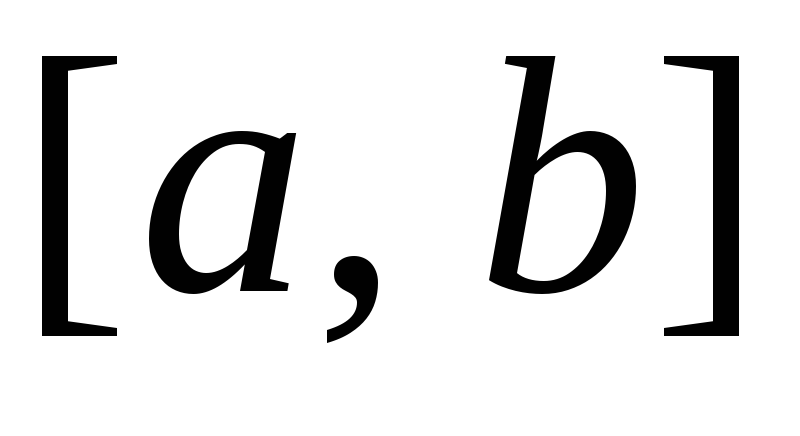 и
и
 ,
то
,
то
![]() .
.
-
(теорема о среднем). Если функция
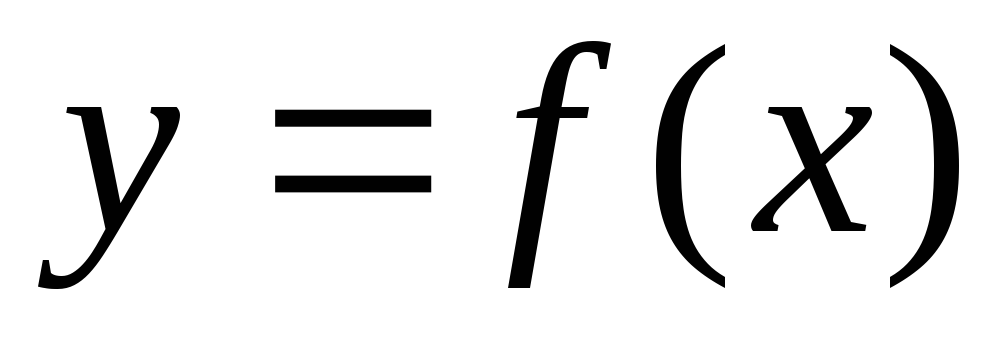 непрерывна на отрезке
непрерывна на отрезке
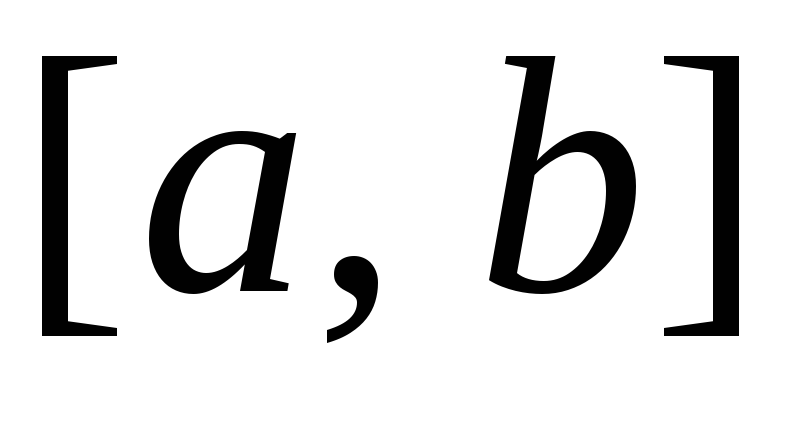 ,
то на этом отрезке существует точка
,
то на этом отрезке существует точка
 ,
такая, что
,
такая, что
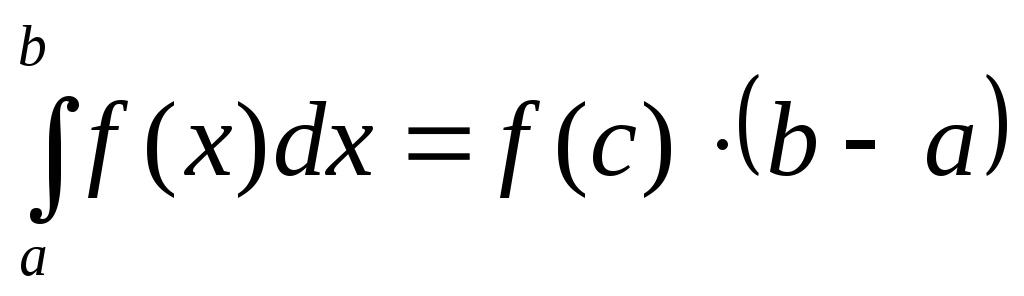 .
.
4. Формула Ньютона–Лейбница
Вычисление определенных интегралов через предел интегральных сумм связано с большими трудностями. Поэтому существует другой метод, основанный на тесной связи, существующей между понятиями определенного и неопределенного интегралов.
Теорема
2. Если
функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() и
и
![]() – какая-либо ее первообразная на этом
отрезке, то справедлива следующая
формула:
– какая-либо ее первообразная на этом
отрезке, то справедлива следующая
формула:
![]() ,
(2)
,
(2)
которая называется
формулой
Ньютона–Лейбница.
Разность
![]() принято записывать следующим образом:
принято записывать следующим образом:
![]() ,
,
где символ![]() называется знаком двойной подстановки.
называется знаком двойной подстановки.
Таким образом, формулу (2) можно записать в виде:
![]() .
.
Нахождение
определенных интегралов с помощью
формулы Ньютона-Лейбница осуществляется
в два этапа: на первом этапе находят
некоторую первообразную
![]() для подынтегральной функции
для подынтегральной функции
![]() ;
на втором –находится разность
;
на втором –находится разность
![]() значений этой первообразной на концах
отрезка
значений этой первообразной на концах
отрезка
![]() .
.
Пример
1.
Вычислить интеграл
![]() .
.
Решение.
Для подынтегральной функции
![]() произвольная первообразная имеет вид
произвольная первообразная имеет вид
![]() .
Так как в формуле Ньютона-Лейбни-ца
можно использовать любую первообразную,
то для вычисления ин-
теграла возьмем
первообразную, имеющую наиболее простой
вид:
.
Так как в формуле Ньютона-Лейбни-ца
можно использовать любую первообразную,
то для вычисления ин-
теграла возьмем
первообразную, имеющую наиболее простой
вид:
![]() .
Тогда
.
Тогда
![]() .
.
Пример
2.
Вычислить интеграл
 .
.
Решение. По формуле Ньютона-Лейбница имеем:
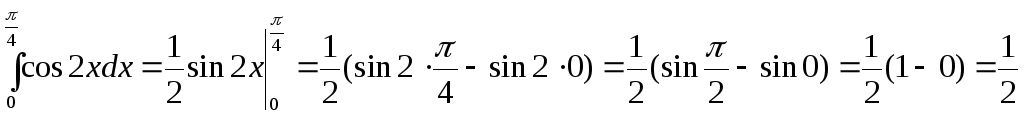 .
.
5. Замена переменной в определенном интеграле
Теорема
3. Пусть
функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() .
Тогда, если:
1) функция
.
Тогда, если:
1) функция
![]() и ее производная
и ее производная
![]() непрерывны при
непрерывны при
![]() ;
2) множеством
значений функции
;
2) множеством
значений функции
![]() при
при
![]() является отрезок
является отрезок
![]() ;
3)
;
3)
![]() ,
,
![]() ,
то справедлива
формула
,
то справедлива
формула
![]() ,
(3)
,
(3)
которая называется формулой замены переменной в определенном интеграле.
Заметим, что как
и в случае неопределенного интеграла,
использование замены переменной
позволяет упростить исходный интеграл,
приблизив его к табличному. При этом в
отличие от неопределенного интеграла
в данном случае нет необходимости
возвращаться к исходной переменной
интегрирования – достаточно лишь найти
новые пределы интегрирования
![]() и
и
![]() (для этого надо решить относительно
переменной t
уравнения
(для этого надо решить относительно
переменной t
уравнения
![]() и
и
![]() )).
)).
На практике часто
вместо подстановки
![]() используют подстановку
используют подстановку
![]() .
В этом случае нахождение новых пределов
интегрирования по переменной t
упрощается:
.
В этом случае нахождение новых пределов
интегрирования по переменной t
упрощается:
![]() ,
,
![]() .
.
Пример
3.
Вычислить интеграл
![]()
Решение.
Введем новую переменную по формуле
![]() .
Определим
.
Определим
![]() и
и
![]() .
Возведя в квадрат обе части равенства
.
Возведя в квадрат обе части равенства
![]() ,
получим
,
получим
![]() ,
откуда
,
откуда
![]()
![]() .
Находим новые пределы интегрирования.
Для этого в формулу
.
Находим новые пределы интегрирования.
Для этого в формулу![]() подставим старые пределы
подставим старые пределы
![]() и
и
![]() .
Получим:
.
Получим:
![]() ,
откуда
,
откуда
![]() и, следовательно,
и, следовательно,
![]() ;
;
![]() ,
откуда
,
откуда
![]() и, следовательно,
и, следовательно,
![]() .
Таким образом:
.
Таким образом:
![]()
![]() .
.
Пример
4.
Вычислить интеграл
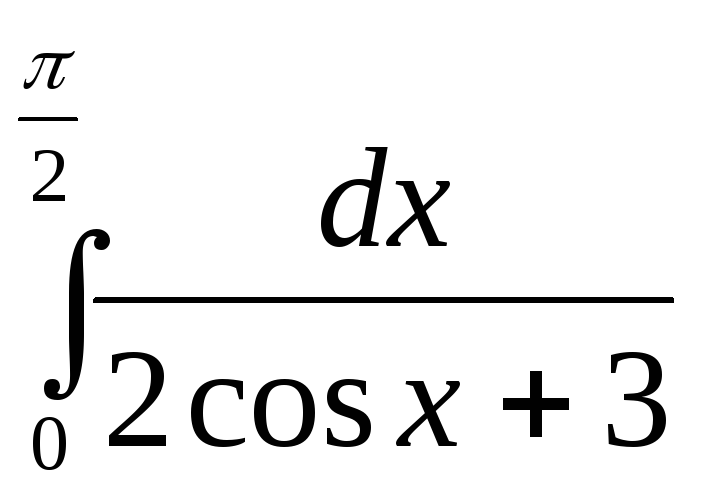 .
.
Решение.
Воспользуемся
универсальной тригонометрической
подстановкой. Положим
![]() ,
откуда
,
откуда
![]()
![]() ,
,
![]() .
Найдем новые пределы интегрирования:
если
.
Найдем новые пределы интегрирования:
если
![]() ,
то
,
то
![]() ;
если
;
если
![]() ,
то
,
то
![]() .
Значит,
.
Значит,
![]() .
Следовательно:
.
Следовательно:
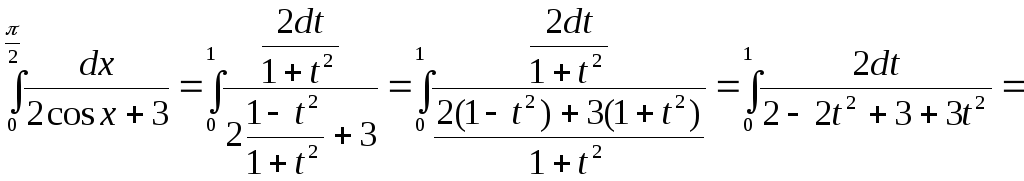
![]()
![]() .
.
Пример
5.
Вычислить интеграл
![]() .
.
Решение.
Положим
![]() ,
тогда
,
тогда
![]() ,
откуда
,
откуда
![]() .
Находим новые пределы интегрирования:
.
Находим новые пределы интегрирования:
![]() ;
;
![]() .
Имеем:
.
Имеем:
![]() .
Следовательно:
.
Следовательно:
![]()
![]() .
.
