
- •Лекция 1 предел последовательности
- •1 Понятие числовой последовательности. Предел числовой последовательности. Свойства сходящихся числовых последовательностей
- •Свойства сходящихся последовательностей
- •2 Бесконечно большие и бесконечно малые числовые последовательности. Основные способы вычисления пределов
- •Свойства бесконечно больших и бесконечно малых последовательностей:
- •Основные способы вычисления пределов:
- •Лекция 2 предел функции
- •1 Предел функции в точке. Односторонние пределы. Предел функции в бесконечности
- •2 Бесконечно малые и бесконечно большие функции. Замечательные пределы
- •Свойства бесконечно малых и бесконечно больших функций
- •Первый и второй замечательные пределы
- •3 Непрерывность функции в точке и на отрезке. Точки разрыва функции и их классификация
- •Свойства функций, непрерывных в точке:
- •Непрерывность функции на отрезке
- •Свойства функций, непрерывных на отрезке
- •Точки разрыва функции и их классификация
- •Лекция 3 производная функции
- •1 Производная функции, ее геометрический и экономический смысл. Основные правила дифференцирования. Производные основных элементарных функций
- •Основные правила дифференцирования
- •2 Логарифмическое дифференцирование. Производная неявной функции. Производные высших порядков
- •Лекция 4 правило лопиталя. Дифференциал функции
- •1 Раскрытие неопределенностей при помощи правила Лопиталя
- •2 Дифференциал функции, его геометрический смысл. Применение дифференциала в приближенных вычислениях
- •Лекция 5 исследование функций
- •1 Локальные экстремумы функции. Достаточные условия экстремума функции
- •2 Исследование функций на выпуклость и вогнутость. Точка перегиба
- •3 Асимптоты графика функции
- •4 Общая схема построения графика функции
- •Лекция 6 функции нескольких переменных
- •1 Предел и непрерывность функции двух переменных
- •2 Частные производные первого порядка. Полный дифференциал. Частные производные высших порядков
- •3 Экстремум функции нескольких переменных. Необходимые и достаточные условия существования экстремума
- •Лекция 7 НеоПределенный иНтеграл
- •1 Первообразная и неопределенный интеграл. Таблица основных неопределенных интегралов
- •Основные свойства неопределенного интеграла
- •2 Основные методы интегрирования
- •Лекция 8 НеоПределенный иНтеграл (продолжение)
- •1 Интегрирование выражений, содержащих квадратный трехчлен
- •2 Интегрирование простейших рациональных дробей. Интегрирование простейших иррациональных функций
- •Интегрирование простейших иррациональных функций
- •3 Интегрирование тригонометрических функций
- •Лекция 9 оПределенный иНтеграл
- •1 Определенный интеграл и его геометрический смысл. Основные свойства определенного интеграла
- •Геометрический смысл определенного интеграла
- •Основные свойства определенного интеграла
- •Формула Ньютона-Лейбница
- •2 Основные способы вычисления определенного интеграла Замена переменной в определенном интеграле
- •Интегрирование по частям
- •Доказательство
- •3 Вычисление площадей плоских фигур, объемов тел вращения, длин дуг плоских кривых Площадь криволинейной трапеции
- •Объем тела вращения
- •Длина дуги плоской кривой
- •Лекция 10 несобственные интегралы
- •1 Несобственные интегралы с бесконечными пределами интегрирования
- •2 Несобственные интегралы от неограниченных функций
- •Лекция 11 дифференциальные уравнения первого порядка
- •1 Дифференциальные уравнения первого порядка. Задача Коши
- •2 Дифференциальные уравнения с разделяющимися переменными
- •3 Линейные дифференциальные уравнения первого порядка
- •1 Метод подстановки (метод Бернулли).
- •2 Метод вариации произвольной постоянной (метод Лагранжа)
- •Лекция 12 дифференциальные уравнения высших порядков
- •1 Интегрирование дифференциальных уравнений высших порядков, допускающих понижение порядка
- •2 Однородные и неоднородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Лекция 13 числовые ряды
- •Числовой ряд. Сходимость. Признаки сходимости
- •1 Определение числового ряда. Сходимость. Основные свойства числовых рядов
- •Основные свойства числовых рядов
- •2 Ряды с положительными членами. Признаки сходимости
- •3 Знакочередующиеся и знакопеременные ряды
- •Лекция 14 степенные ряды
- •Ключевые понятия
- •1 Определение степенного ряда. Теорема Абеля
- •2 Свойства степенных рядов
- •3. Ряды Тейлора, Маклорена для функций
- •Разложение некоторых элементарных функций в ряд Маклорена
- •Приложения степенных рядов
- •Список литературы
- •Содержание
- •Лекция 13 Числовые ряды………….……………………………………..93
- •Лекция 14 Степенные ряды……………………...……….………………103
- •Список литературы…………..…………….……...………………………..112
- •220086, Минск, ул. Славинского, 1, корп. 3.
1 Первообразная и неопределенный интеграл. Таблица основных неопределенных интегралов
Одной
из основных задач дифференциального
исчисления является отыскание производной
заданной функции. В интегральном
исчислении решается обратная задача:
по данной функции
![]() найти функцию
найти функцию
![]() ,
производная которой была бы равна
функции
,
производная которой была бы равна
функции
![]() ,
т.е.
,
т.е.
![]() .
Искомую функцию
.
Искомую функцию
![]() называют первообразной
для функции
называют первообразной
для функции
![]() .
.
Определение
1 Функция
![]() называется первообразной для функции
называется первообразной для функции
![]() на интервале
на интервале
![]() ,
если она дифференцируема на
,
если она дифференцируема на
![]() и для любого
и для любого
![]() выполняется равенство
выполняется равенство
![]() .
.
Теорема:
если функция
![]() является первообразной для функции
является первообразной для функции
![]() на интервале
на интервале
![]() ,
то множество всех первообразных для
,
то множество всех первообразных для
![]() задается формулой
задается формулой
![]() ,
где C
– произвольная постоянная.
,
где C
– произвольная постоянная.
Определение
2 Множество
всех первообразных функций
![]() для функции
для функции
![]() на интервале
на интервале
![]() называется неопределенным интегралом
от функции
называется неопределенным интегралом
от функции
![]() на этом интервале и обозначается
символом
на этом интервале и обозначается
символом
![]() ,
где
,
где
![]() –
знак интеграла;
–
знак интеграла;
![]() –
подынтегральная функция;
–
подынтегральная функция;
![]() –
подынтегральное
выражение;
–
подынтегральное
выражение;
![]() – переменная
интегрирования.
– переменная
интегрирования.
Таким образом:
![]() ,
,
где
![]() – некоторая первообразная для
– некоторая первообразная для
![]() на интервале
на интервале
![]() ;
;
C – произвольная постоянная.
Операция нахождения неопределенного интеграла от данной функции называется интегрированием этой функции. Интегрирование представляет собой операцию, обратную дифференцированию. Для того чтобы проверить, правильно ли выполнено интегрирование, достаточно продифференцировать результат и получить при этом подынтегральную функцию.
Пример
1 Проверить,
что
![]() .
.
Решение. Продифференцируем результат интегрирования:
![]() .
.
Получили подынтегральную функцию, следовательно, интегрирование выполнено верно.
Основные свойства неопределенного интеграла
Из определения неопределенного интеграла непосредственно вытекают следующие его свойства:
-
Производная от неопределенного интеграла равна подын-тегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению:
![]() .
.
-
Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
![]() .
.
-
Постоянный множитель можно выносить за знак неопределенного интеграла:
![]() (c
– const).
(c
– const).
-
Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме неопределенных интегралов:
![]() .
.
Заметим, что данное свойство справедливо для любого конечного числа слагаемых.
-
Если
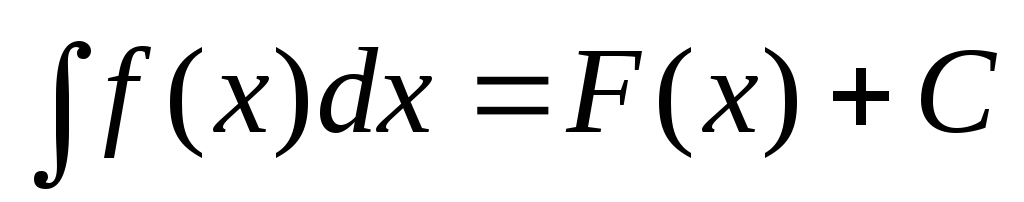 ,
а
,
а
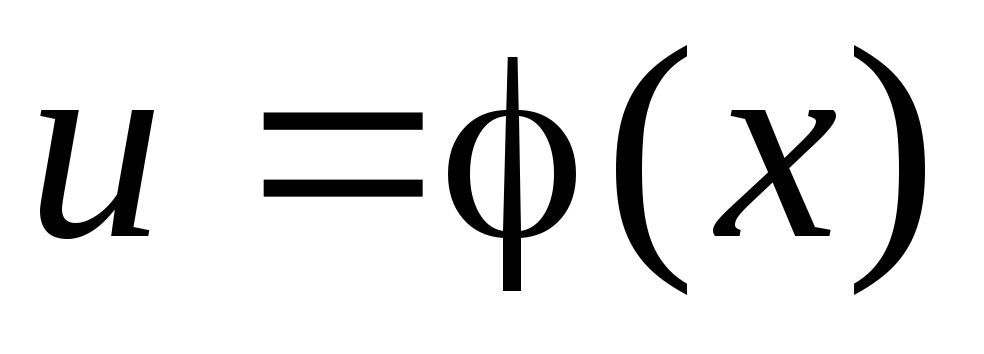 – произвольная функция, имеющая
непрерывную производную, то
– произвольная функция, имеющая
непрерывную производную, то .
.
Таблица основных неопределенных интегралов
Данную таблицу можно получить исходя из того, что интегрирование представляет собой операцию, противоположную дифференцированию. Часть формул этой таблицы непосредственно следует из таблицы производных основных элементарных функций. Справедливость остальных формул легко проверяется дифференцированием.
-
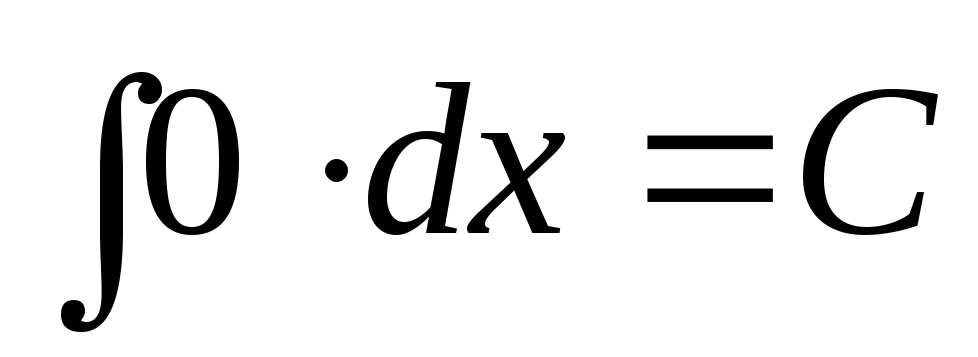 .
. -
 .
. -
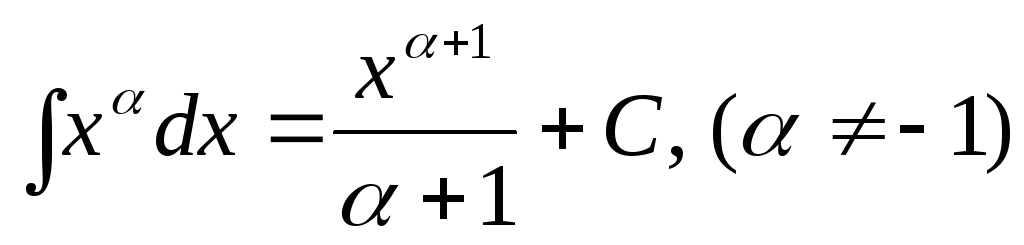 .
. -
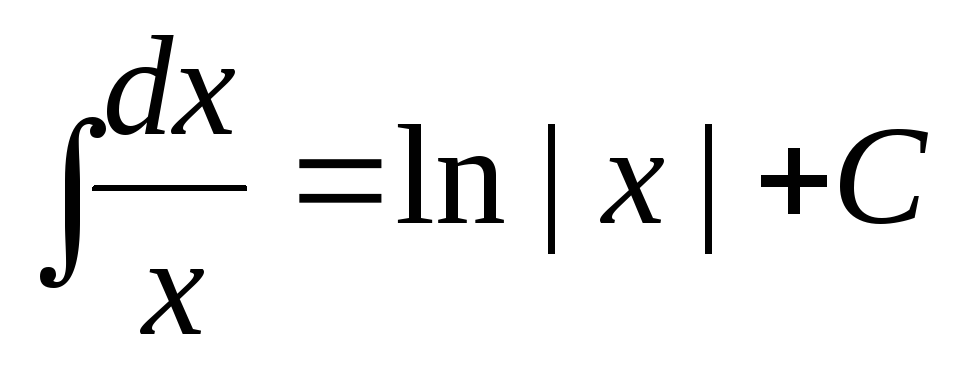 .
. -
 .
. -
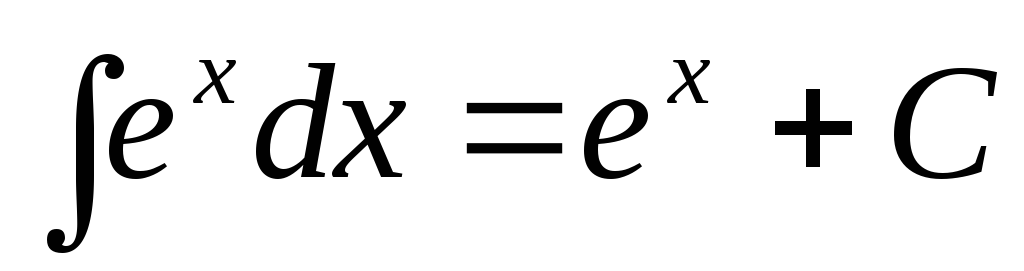 .
. -
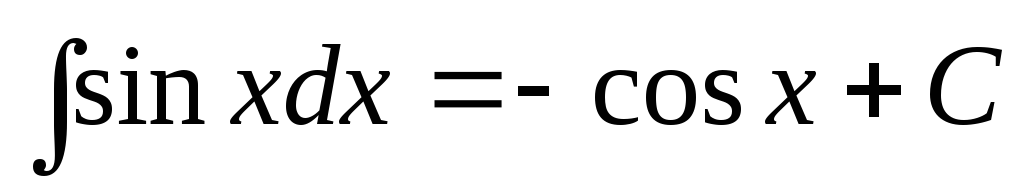 .
. -
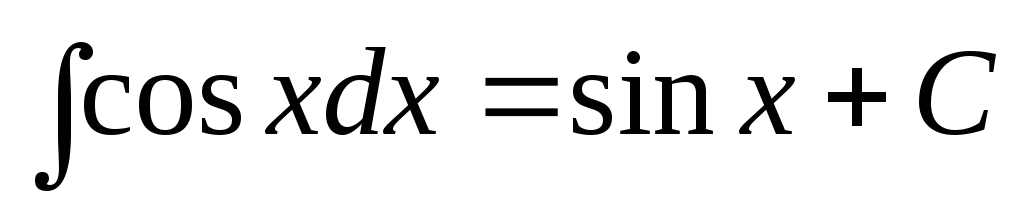 .
. -
 .
. -
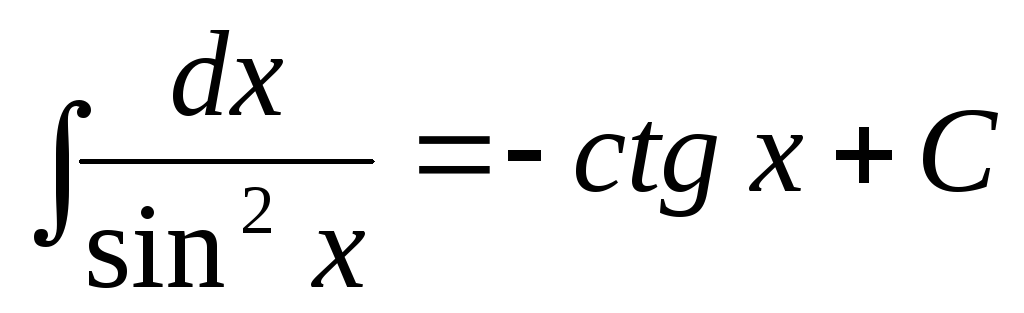 .
. -
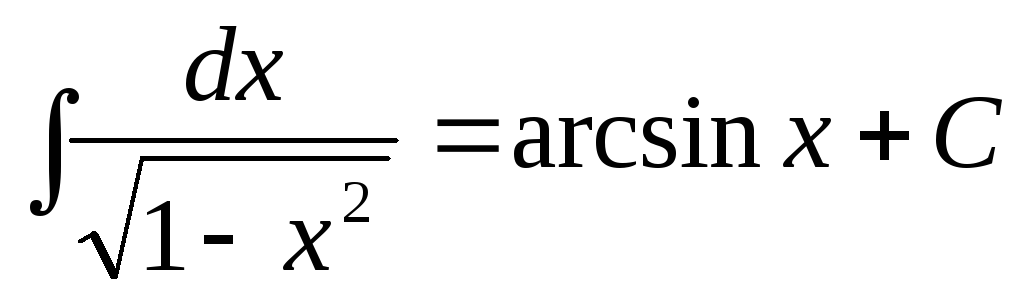 .
. -
 ,
а
0.
,
а
0. -
 ,
а
0.
,
а
0. -
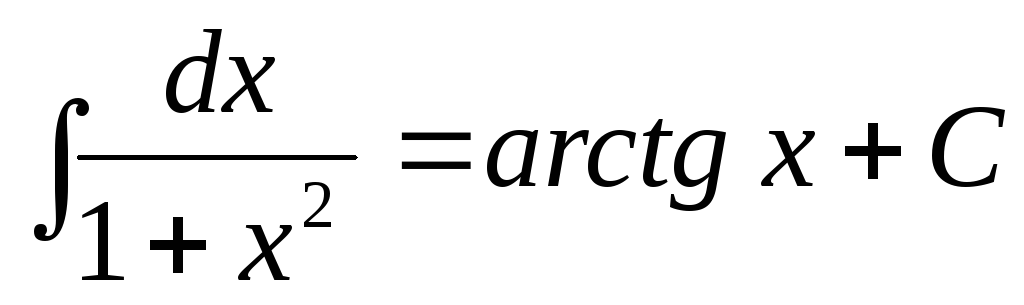 .
. -
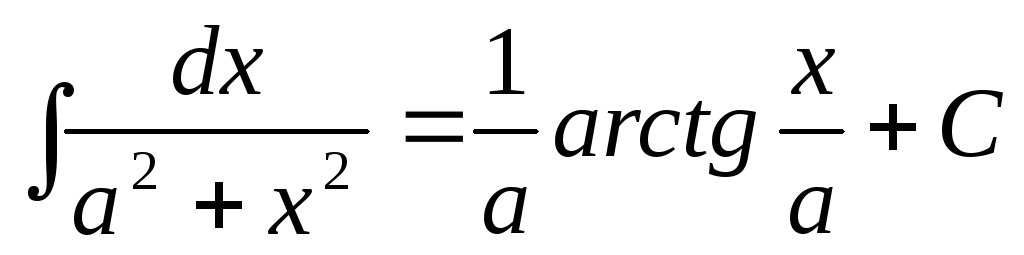 ,
а
0.
,
а
0. -
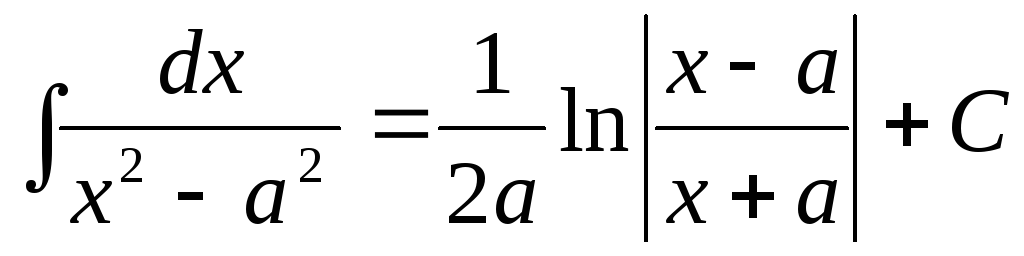 ,
а
0.
,
а
0.
