
- •Лекция 1 предел последовательности
- •1 Понятие числовой последовательности. Предел числовой последовательности. Свойства сходящихся числовых последовательностей
- •Свойства сходящихся последовательностей
- •2 Бесконечно большие и бесконечно малые числовые последовательности. Основные способы вычисления пределов
- •Свойства бесконечно больших и бесконечно малых последовательностей:
- •Основные способы вычисления пределов:
- •Лекция 2 предел функции
- •1 Предел функции в точке. Односторонние пределы. Предел функции в бесконечности
- •2 Бесконечно малые и бесконечно большие функции. Замечательные пределы
- •Свойства бесконечно малых и бесконечно больших функций
- •Первый и второй замечательные пределы
- •3 Непрерывность функции в точке и на отрезке. Точки разрыва функции и их классификация
- •Свойства функций, непрерывных в точке:
- •Непрерывность функции на отрезке
- •Свойства функций, непрерывных на отрезке
- •Точки разрыва функции и их классификация
- •Лекция 3 производная функции
- •1 Производная функции, ее геометрический и экономический смысл. Основные правила дифференцирования. Производные основных элементарных функций
- •Основные правила дифференцирования
- •2 Логарифмическое дифференцирование. Производная неявной функции. Производные высших порядков
- •Лекция 4 правило лопиталя. Дифференциал функции
- •1 Раскрытие неопределенностей при помощи правила Лопиталя
- •2 Дифференциал функции, его геометрический смысл. Применение дифференциала в приближенных вычислениях
- •Лекция 5 исследование функций
- •1 Локальные экстремумы функции. Достаточные условия экстремума функции
- •2 Исследование функций на выпуклость и вогнутость. Точка перегиба
- •3 Асимптоты графика функции
- •4 Общая схема построения графика функции
- •Лекция 6 функции нескольких переменных
- •1 Предел и непрерывность функции двух переменных
- •2 Частные производные первого порядка. Полный дифференциал. Частные производные высших порядков
- •3 Экстремум функции нескольких переменных. Необходимые и достаточные условия существования экстремума
- •Лекция 7 НеоПределенный иНтеграл
- •1 Первообразная и неопределенный интеграл. Таблица основных неопределенных интегралов
- •Основные свойства неопределенного интеграла
- •2 Основные методы интегрирования
- •Лекция 8 НеоПределенный иНтеграл (продолжение)
- •1 Интегрирование выражений, содержащих квадратный трехчлен
- •2 Интегрирование простейших рациональных дробей. Интегрирование простейших иррациональных функций
- •Интегрирование простейших иррациональных функций
- •3 Интегрирование тригонометрических функций
- •Лекция 9 оПределенный иНтеграл
- •1 Определенный интеграл и его геометрический смысл. Основные свойства определенного интеграла
- •Геометрический смысл определенного интеграла
- •Основные свойства определенного интеграла
- •Формула Ньютона-Лейбница
- •2 Основные способы вычисления определенного интеграла Замена переменной в определенном интеграле
- •Интегрирование по частям
- •Доказательство
- •3 Вычисление площадей плоских фигур, объемов тел вращения, длин дуг плоских кривых Площадь криволинейной трапеции
- •Объем тела вращения
- •Длина дуги плоской кривой
- •Лекция 10 несобственные интегралы
- •1 Несобственные интегралы с бесконечными пределами интегрирования
- •2 Несобственные интегралы от неограниченных функций
- •Лекция 11 дифференциальные уравнения первого порядка
- •1 Дифференциальные уравнения первого порядка. Задача Коши
- •2 Дифференциальные уравнения с разделяющимися переменными
- •3 Линейные дифференциальные уравнения первого порядка
- •1 Метод подстановки (метод Бернулли).
- •2 Метод вариации произвольной постоянной (метод Лагранжа)
- •Лекция 12 дифференциальные уравнения высших порядков
- •1 Интегрирование дифференциальных уравнений высших порядков, допускающих понижение порядка
- •2 Однородные и неоднородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Лекция 13 числовые ряды
- •Числовой ряд. Сходимость. Признаки сходимости
- •1 Определение числового ряда. Сходимость. Основные свойства числовых рядов
- •Основные свойства числовых рядов
- •2 Ряды с положительными членами. Признаки сходимости
- •3 Знакочередующиеся и знакопеременные ряды
- •Лекция 14 степенные ряды
- •Ключевые понятия
- •1 Определение степенного ряда. Теорема Абеля
- •2 Свойства степенных рядов
- •3. Ряды Тейлора, Маклорена для функций
- •Разложение некоторых элементарных функций в ряд Маклорена
- •Приложения степенных рядов
- •Список литературы
- •Содержание
- •Лекция 13 Числовые ряды………….……………………………………..93
- •Лекция 14 Степенные ряды……………………...……….………………103
- •Список литературы…………..…………….……...………………………..112
- •220086, Минск, ул. Славинского, 1, корп. 3.
Геометрический смысл определенного интеграла
Пусть
на отрезке
![]() задана
непрерывная неотрицательная функция
задана
непрерывная неотрицательная функция
![]() .
Криволинейной
трапецией называется фигура, ограниченная
сверху графиком функции y
= f(x),
снизу – осью Ох, слева и справа – прямыми
x
= a
и x
= b.
.
Криволинейной
трапецией называется фигура, ограниченная
сверху графиком функции y
= f(x),
снизу – осью Ох, слева и справа – прямыми
x
= a
и x
= b.
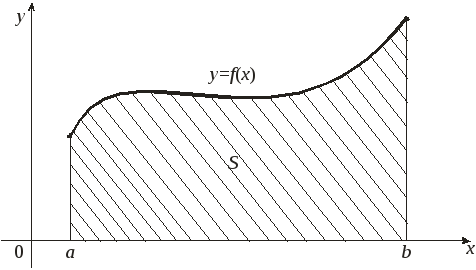
Определенный
интеграл
![]() от неотрицательной функции
от неотрицательной функции
![]() ,
с геометрической точки зрения, численно
равен площади криволинейной трапеции,
ограниченной сверху графиком функции
,
с геометрической точки зрения, численно
равен площади криволинейной трапеции,
ограниченной сверху графиком функции
![]() ,
слева и справа – отрезками прямых
,
слева и справа – отрезками прямых
![]() и
и
![]() ,
снизу – отрезком
,
снизу – отрезком
![]() оси Ох.
оси Ох.
Основные свойства определенного интеграла
1
Значение определенного интеграла не
зависит от обозначения переменной
интегрирования:
![]() .
.
2
Определенный интеграл с одинаковыми
пределами интегрирования равен нулю:
![]()
3
![]()
4
Постоянный
множитель можно выносить за знак
определенного интеграла:
![]() ,
с
– const.
,
с
– const.
5 Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме определенных интегралов от этих функций:
![]() .
.
6
Если функция
![]() интегрируема на отрезке
интегрируема на отрезке
![]() и
и
![]() ,
то
,
то
![]() .
.
7
(теорема о
среднем).
Если функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() ,
то на этом отрезке существует точка
,
то на этом отрезке существует точка
![]() ,
такая, что
,
такая, что
![]() .
.
Формула Ньютона-Лейбница
Теорема
2 Если функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() и
и
![]() – какая-либо ее первообразная на этом
отрезке, то справедлива следующая
формула:
– какая-либо ее первообразная на этом
отрезке, то справедлива следующая
формула:
![]() ,
(2)
,
(2)
которая называется формулой Ньютона-Лейбница.
Нахождение
определенных интегралов с помощью
формулы Ньютона-Лейбница осуществляется
в два этапа: на первом этапе находят
некоторую первообразную
![]() для подынтегральной функции
для подынтегральной функции
![]() ;
на втором –разность
;
на втором –разность
![]() значений этой первообразной на концах
отрезка
значений этой первообразной на концах
отрезка
![]() .
.
Пример
1 Вычислить
интеграл
![]() .
.
Решение.
Для подынтегральной функции
![]() произвольная первообразная имеет вид
произвольная первообразная имеет вид
![]() .
Так как в формуле Ньютона-Лейбница
можно использовать любую первообразную,
то для вычисления интеграла возьмем
первообразную, имеющую наиболее простой
вид:
.
Так как в формуле Ньютона-Лейбница
можно использовать любую первообразную,
то для вычисления интеграла возьмем
первообразную, имеющую наиболее простой
вид:
![]() .
Тогда
.
Тогда
![]() .
.
Пример
2 Вычислить
интеграл
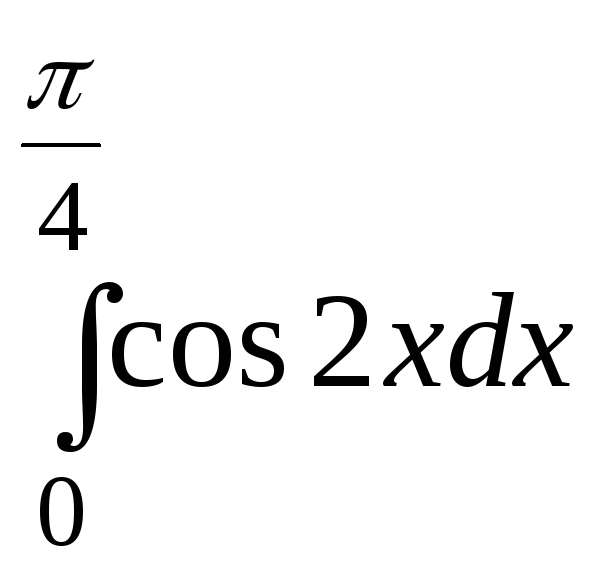 .
.
Решение. По формуле Ньютона-Лейбница имеем:
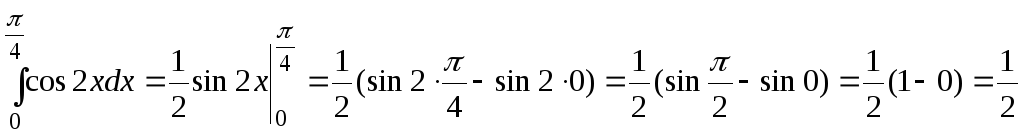 .
.
2 Основные способы вычисления определенного интеграла Замена переменной в определенном интеграле
Теорема
3 Пусть
функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() .
Тогда, если: 1) функция
.
Тогда, если: 1) функция
![]() и ее производная
и ее производная
![]() непрерывны при
непрерывны при
![]() ;
2) множеством значений функции
;
2) множеством значений функции
![]() при
при
![]() является отрезок
является отрезок
![]() ;
3)
;
3)
![]() ,
,
![]() ,
то справедлива формула
,
то справедлива формула
![]() ,
(3)
,
(3)
которая называется формулой замены переменной в определенном интеграле.
Заметим,
что как и в случае неопределенного
интеграла, использование замены
переменной позволяет упростить исходный
интеграл, приблизив его к табличному.
При этом в отличие от неопределенного
интеграла в данном случае нет необходимости
возвращаться к исходной переменной
интегрирования – достаточно лишь найти
новые пределы интегрирования
![]() и
и
![]() (для этого надо решить относительно
переменной t
уравнения
(для этого надо решить относительно
переменной t
уравнения
![]() и
и
![]() )).
)).
Пример
3 Вычислить
интеграл
![]() .
.
Решение.
Введем новую переменную по формуле
![]() .
Определим
.
Определим
![]() и
и
![]() .
Возведя в квадрат обе части равенства
.
Возведя в квадрат обе части равенства
![]() ,
получим
,
получим
![]() ,
откуда
,
откуда
![]()
![]() .
Находим новые пределы интегрирования.
Для этого в формулу
.
Находим новые пределы интегрирования.
Для этого в формулу![]() подставим исходные пределы
подставим исходные пределы
![]() и
и
![]() .
Получим:
.
Получим:
![]() ,
откуда
,
откуда
![]() и, следовательно,
и, следовательно,
![]() ;
;
![]() ,
откуда
,
откуда
![]() и, следовательно,
и, следовательно,
![]() .
Таким образом:
.
Таким образом:
![]()
![]() .
.
