Питання для самоперевірки

1) Як будуються графіки моделі та лінії тренду за допомогою Excel?

2) Яким чином будуються рівняння лінійної моделі ?

3) Як обчислюються коефіцієнти квадратичної моделі ?

4) Яким чином обчислюються відхилення даних точок от знайденої залежності ?

5) Як обчислюються коефіцієнти експонентної моделі ?

3. Лабораторна робота №3 „Пошук наближеного рішення нелінейного рівняння ”

Ціль роботи: вивчити наближені методи рішення нелінейних рівнянь , придбати навички рішення рівняння методом дотичних та з використанням Excel

3.1.Теоретичні відомості .

3.1.1. Постановка задачі.

Нехай дано рівняння . Необхідно знайти наближені значення коренів цього рівняння. Будемо припускати, що всі корені ізольовані, тобто кожний з коренів має окіл, що не містить інших коренів. Пошук наближених значень коренів здійснюється в 2 етапи:

1. Відділення відрізків, що містять ізольований корінь.

2. Відшукання наближеного значення кореня з заданою точністю на кожному виділеному відрізку.

Для відділення відрізків з ізольованим коренем, сформулюємо теорему з математичного аналізу:

Th. Якщо функція , неперервна на [a, b], має на кінцях відрізка значення протилежних знаків, тобто, то на [a, b] міститься принаймні один корінь рівняння (рис.3.1). Якщо, крім того, похідна на [a, b], зберігає постійний знак, то корінь єдиний (рис.3.2).

Рис. 3.1. Рис. 3.2.

2. Метод Ньютона (дотичних).

Хай [а, b] відрізок, що містить ізольований корінь рівняння і функція , неперервна на [а, b] разом з першою і другою похідними, причому обидві похідні зберігають постійний знак. Розглянемо окремий випадок.

Хай: ;;;

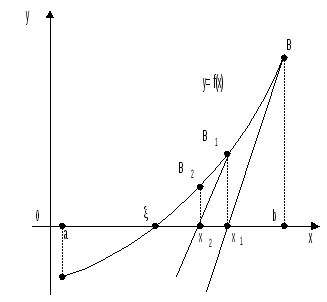
Рис. 3.3. Геометрична інтерпретація методу дотичних

В якості вибираємо точку відрізка [а, b], для якої виконана умова, тобто знак функції в точці співпадає із знаком другої похідної. (на прикладі ). В точці В () проведемо дотичну до кривої .

Як 1-е наближення виберемо абсцису точки перетину дотичної з віссю 0х . В точці В1 () проводимо дотичну і в якості вибираємо абсцису точки перетину дотичної з віссю Ох і т.д. В точці В_n() проводимо дотичну:

Абсциса точки перетину цієї дотичної з віссю Ох дає наближення, тобто підставляючи в рівняння (3), отримаємо .

Th. Нехай безперервна разом з і на відрізку [а,b], що містить єдиний корінь рівняння (1) і обидва похідні зберігають на [а, b] постійний знак. Тоді, виходячи з нульового наближення, що задовольняє умові, можна знайти, використовуючи метод Ньютона, наближене рішення з будь-яким степенем точності.

Похибку наближеного рішення , отриманого по методу Ньютона, визначається формулою:

, де , .

3.2. Приклад виконання лабораторної роботи №3

Відділити корінь рівняння графічно і знайти наближене рішення рівняння методом дотичних з точністю  = 0.005.

Відділимо корінь. Побудуємо графіки функцій і . Абсциса точки їх перетину - точне значення кореня.

Складемо таблицю значень:

x	-1	0	1	2
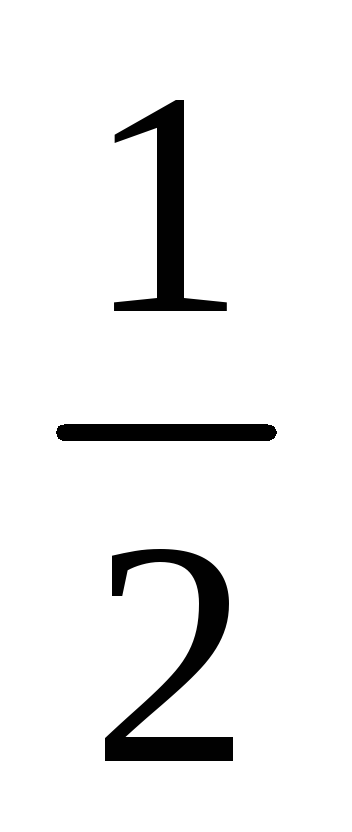
2x		1	2	4
4-х	5	4	3	2

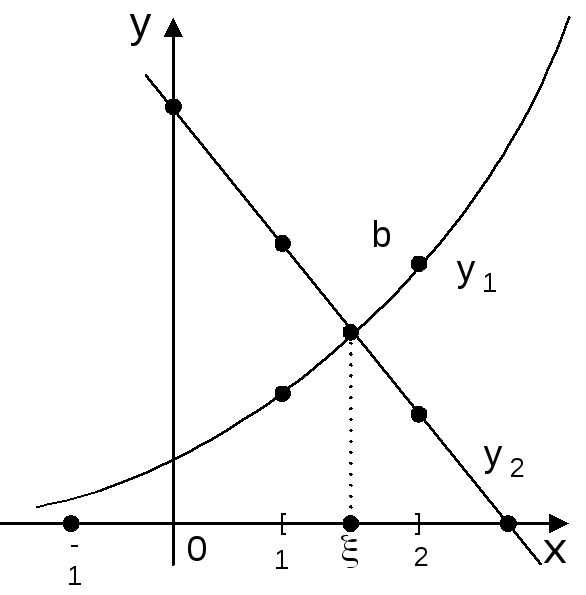
Рис.3. 4. Геометричний метод відділення кореня.

Як видно з рисунка, корінь рівняння укладений в інтервалі [1,2]. Перевіримо це.

Таким чином, відрізок [1,2] містить принаймні 1 корінь. Знайдемо похідні:

Обидві похідні зберігають на відрізку [1,2] постійний знак, отже, корінь єдиний. Виберемо нульове наближення з умови . Оскільки , то в якості вибираємо правий кінець відрізка . Знаходимо перше наближення:

Оцінимо похибку:

Оскільки монотонно зростаюча функція на відрізку [1,2], то

.

Оскільки - так само монотонно зростає на відрізку [1,2], то

.

Тоді .

Обчислимо друге наближення:

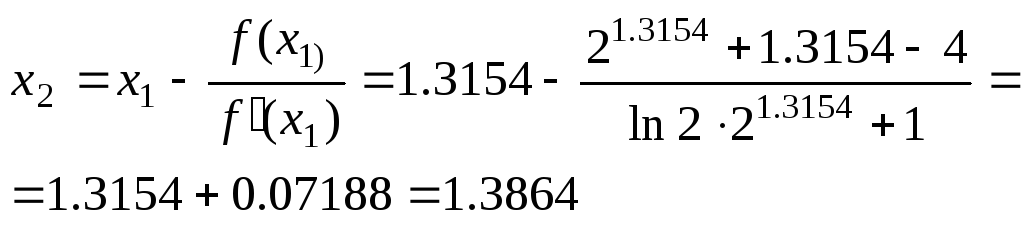
Оцінимо похибку:

.

Оскільки похибка менше заданої точності, то - шукане наближене значення кореня рівняння .