5.2. Приклад виконання лабораторної роботи №5

Знайти наближене рішення системи рівнянь, використовуючи методи ітерацій і Зейделя. Побудувати чотири наближення та знайти похибки наближених рішень.

Нехай дана система рівнянь в виду, зручному для ітерацій

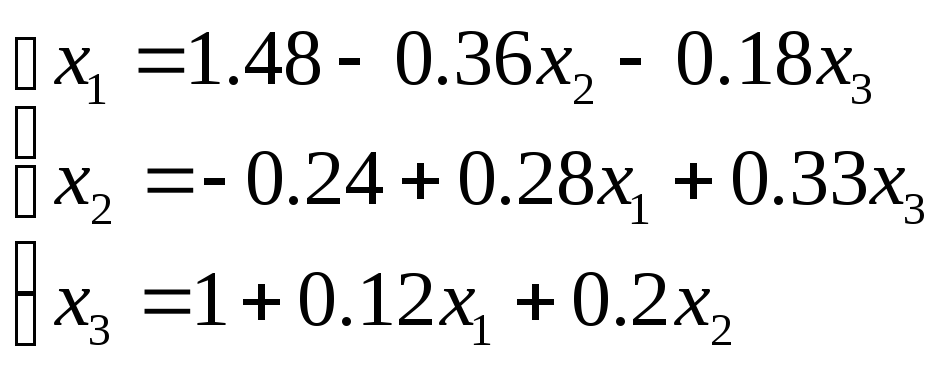
Матриця коефіцієнтів має вигляд:

Обчислимо норму :

.

Отже ітераційний процес буде сходитись до точного рішення .

Вибираємо нульове наближення:

За методом ітерацій побудуємо перше наближення.

Перше наближення :

Знайдемо похибку 1-го наближення :

Обчислимо друге наближення

Знайдемо похибку 2-го наближення

Обчислимо третє наближення

Знайдемо похибку 3-го наближення

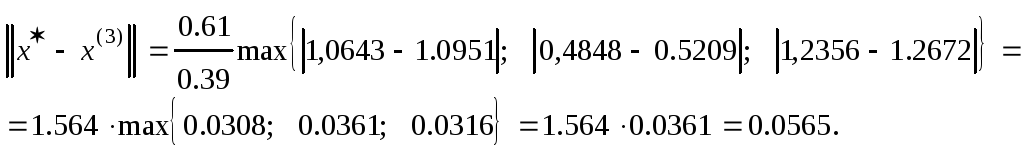
Обчислимо четверте наближення

Знайдемо похибку 4-го наближення

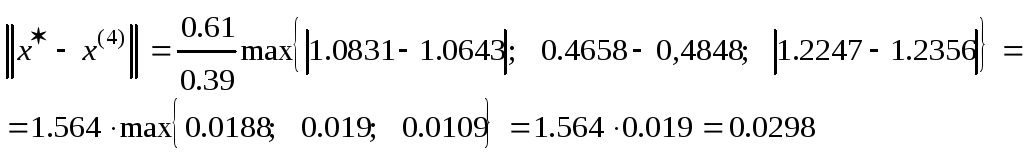
Знайдемо наближене рішення системи рівнянь, використовуючи метод Зейделя.

Вибираємо нульове наближення:

Побудуємо перше наближення:

Знайдемо похибку 1-го наближення :

.

Обчислимо друге наближення

Знайдемо похибку 2-го наближення

.

Обчислимо третє наближення

Знайдемо похибку наближення :

Обчислимо четверте наближення

Знайдемо похибку :

.

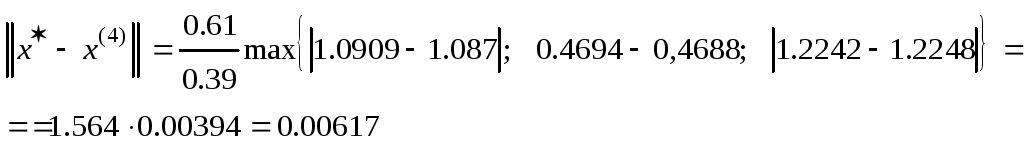
5.3. Завдання до лабораторної роботи №5

Знайти наближене рішення системи рівнянь. Побудувати чотири наближення та знайти похибки наближених рішень. Для парних номеров варантів використовувати метод ітерацій, для непарних номеров варантів - метод Зейделя.

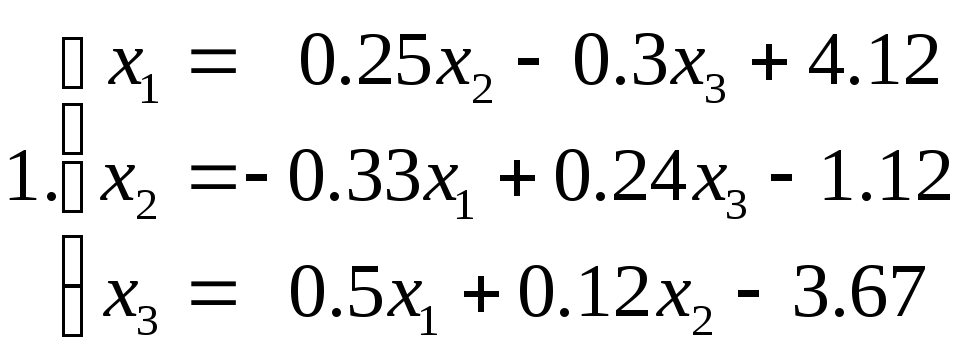
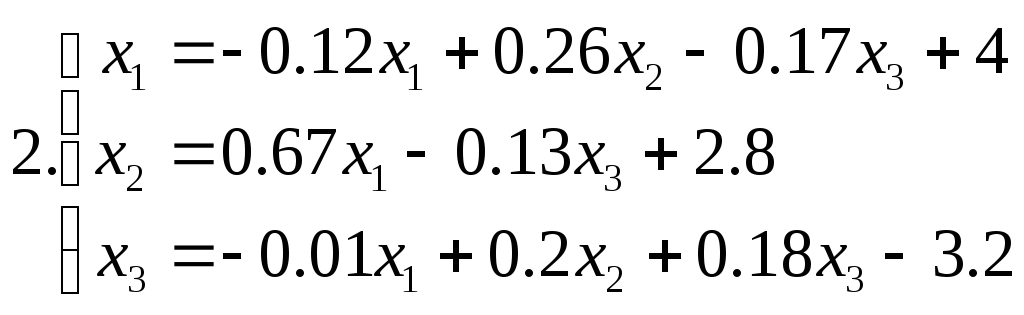
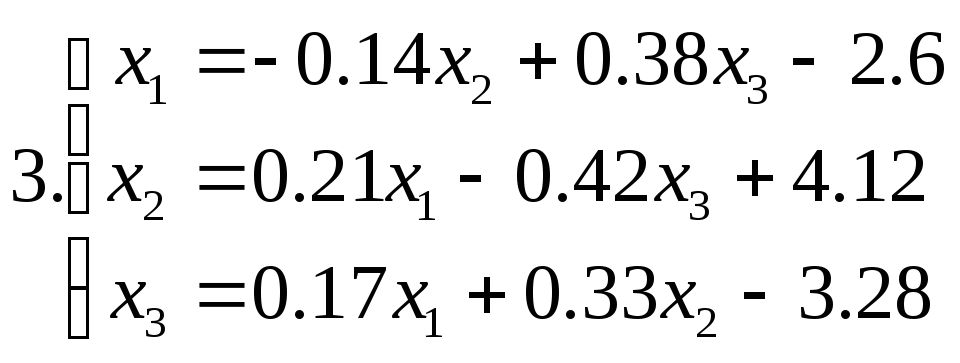
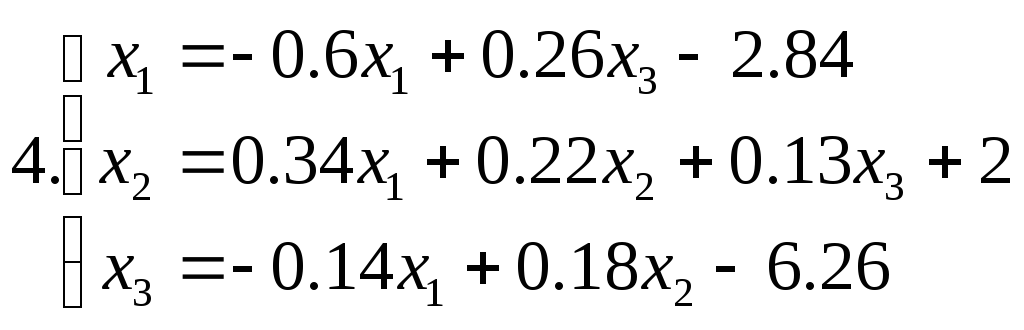
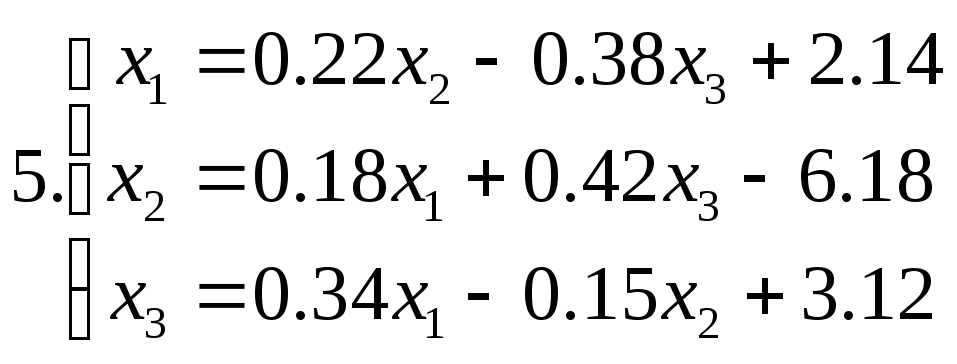
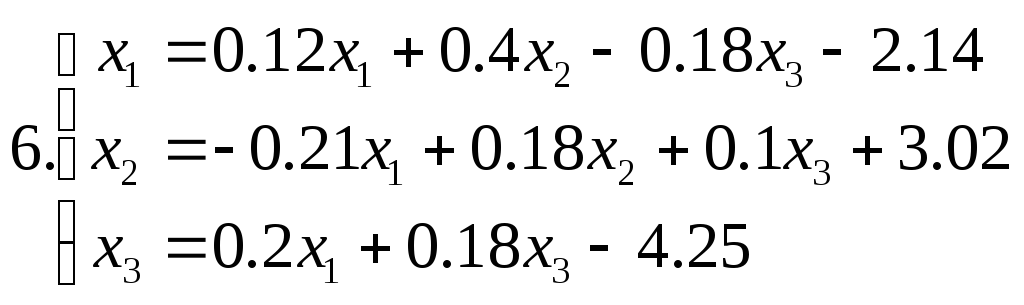
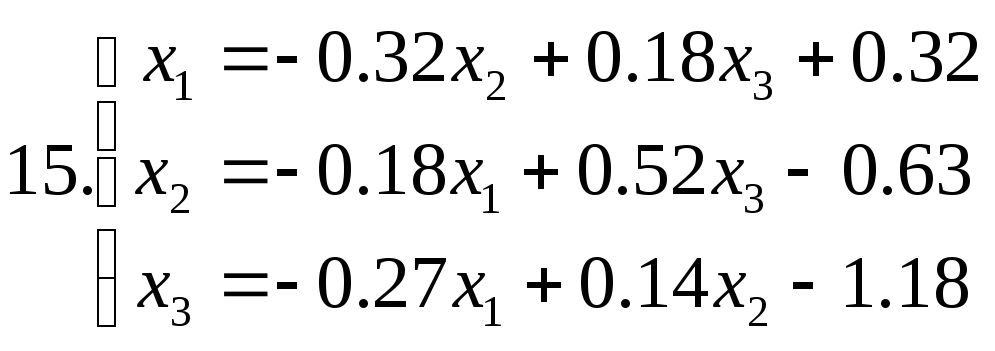
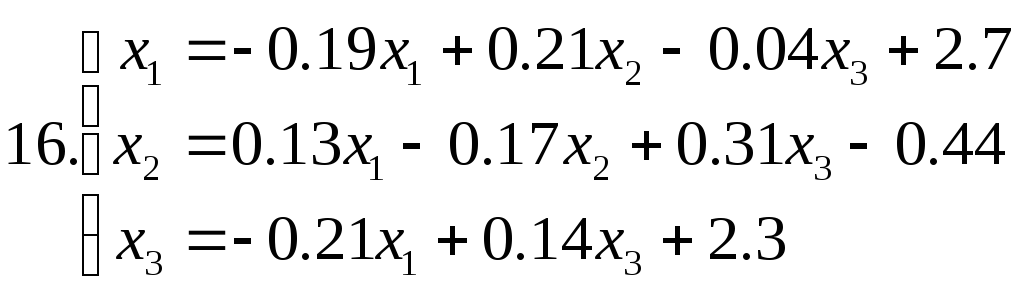
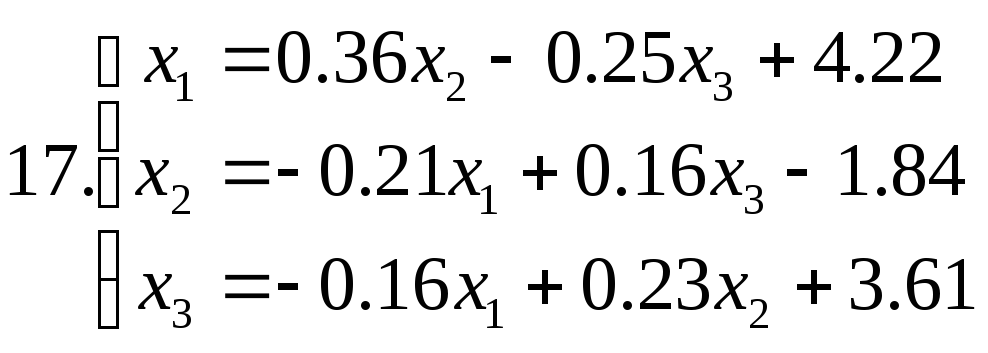
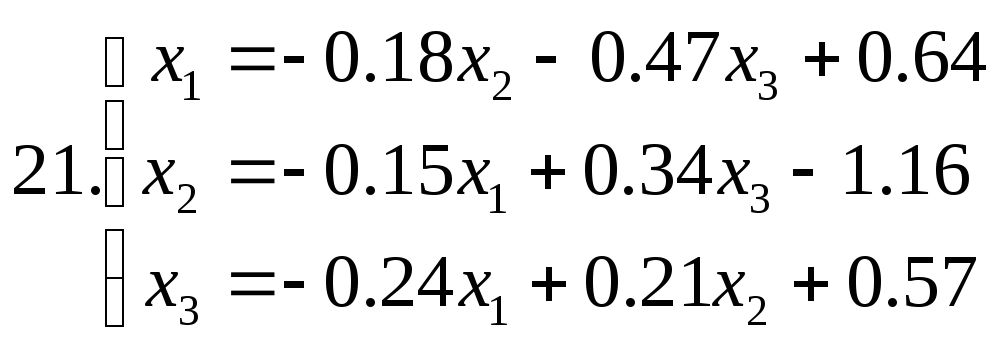
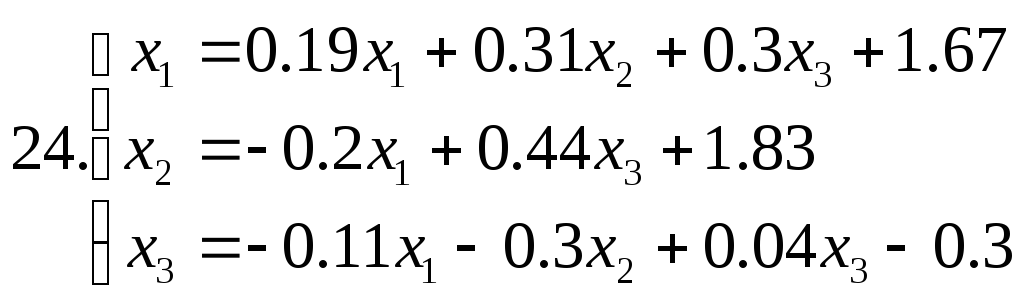
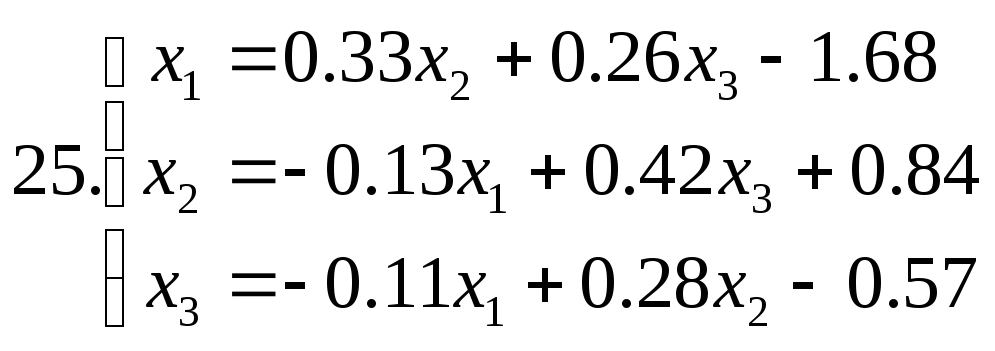
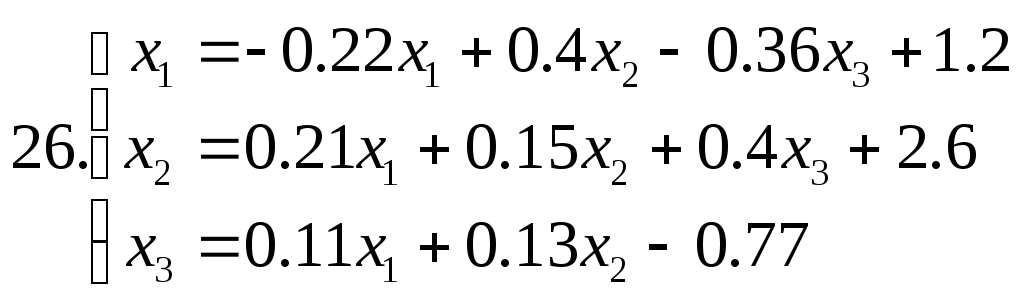
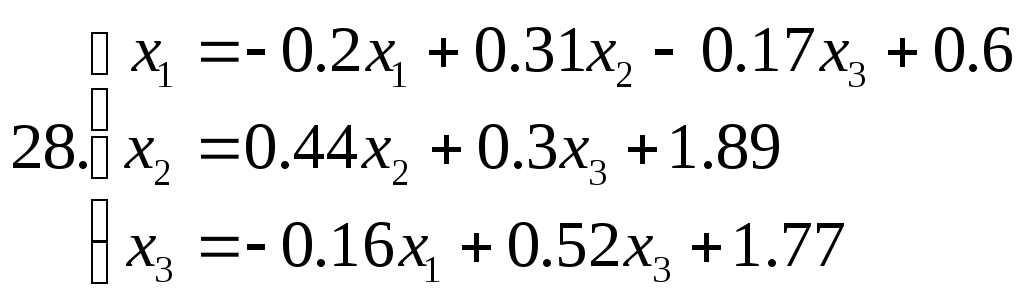
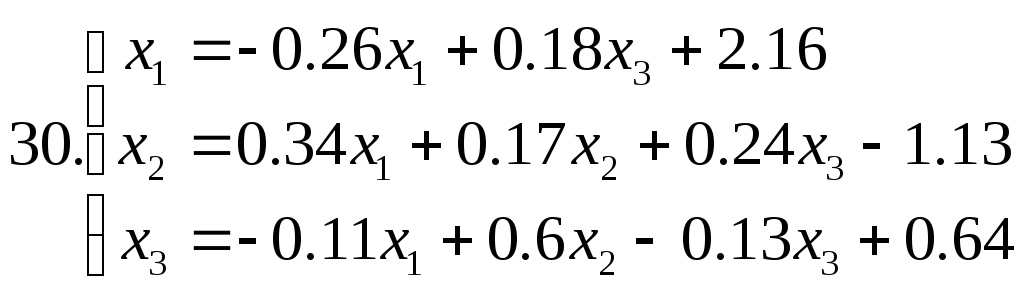
Питання для самоперевірки

1. Як визначаються і обчислюються норма вектора і норма матриці?

2. Яким чином приводиться система до виду, зручному для ітерацій?

3. Як реалізується метод ітерацій?

4. Яким чином оцінюється похибка рішення, отриманого методом ітерацій?

5. Чим відрізняється метод Зейделя від методу ітерацій ?

Використовувана література

1) [1] ст. 19-27; стр. 151-161

2) [2] ст. 4-6; стр. 49-54

3) [3] ст. 29-36

6. Лабораторна робота №6 „Побудува інтерполяційніх многочленів Лагранжа та Ньютона”

Ціль роботи: вивчити методи побудови інтерполяційних многочленів Лагранжа та Ньютона, придбати навички побудови інтерполяційних многочленів та побудови інтерполяційних многочленів з використанням системи MathCAD.

6.1.Теоретичні відомості

6.1.1. Постановка задачі.

Хай відомі значення деякої функції f в різних точках . Позначимо . Наприклад, вони отримані в результаті експерименту. Виникає задача наближеного відновлення функції f в довільній точці х. Для вирішення цієї задачі будується многочлен алгебри ступеня n, який в точках приймає значення , тобто (1)

і називається інтерполяційним. Точки - вузли інтерполяції.

Інтерполяційні многочлени також використовуються для отримання формул чисельного інтегрування і диференціювання.

Теорема існування і єдиності: Існує єдиний інтерполяційний многочлен ступеня n, що задовольняє умові (1).