Питання для самоперевірки

1. Як записується многочлен Лагранжа?

2. Яка погрішність інтерполяційного многочлена?

3. Як виводиться інтерполяційний многочлен Лагранжа для рівновіддалених вузлів?

4. Що називається кінцевою різницею функції 1-го і 2-го порядку?

5. Як будується інтерполяційний многочлен Ньютона через і для інтерполяції «вперед»?

6. Як будуються многочлени Ньютона для інтерполяції «назад через» і ?

Література, що використовується

1) [1] стор. 27-37;стор. 43-55

2) [2] стор. 109-118

3) [3] стор. 6-15

7. Лабораторна робота №7 „Рішення задачі лінійного програмування. ”

Ціль роботи: вивчити методи рішення задачі лінійного програмування, придбати навички рішення задачі лінійного програмування геометричним , симплексним методами та з використанням системи MathCAD.

7.1. Теоретичні відомості

7.1.1. Постановка задачі.

Лінійне програмування - наука, що вивчає методи пошуку мінімального і максимального значення лінійної функції, на невідомі якої накладені лінійні обмеження.

Розглянемо лінійну функцію: (1) Така функція називається цільовою функцією. Нехай на невідомі функції накладені обмеження:

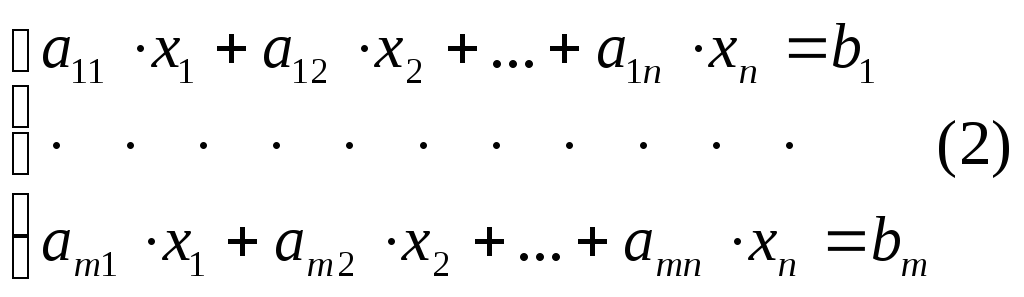
Потрібно знайти такий набір значень невідомих , який задовольняв би системі (2) і мінімізував (максимізував) цільову функцію. Визначення. Безліч значень X , що задовольняє системі обмежень (2), називається областю припустимих рішень. Рішення з цієї області називається планом. У векторному виді задача лінійного програмування має такий вигляд.

Нехай треба мінімізувати (максимізувати) лінійну форму: при обмеженнях: ; де ,

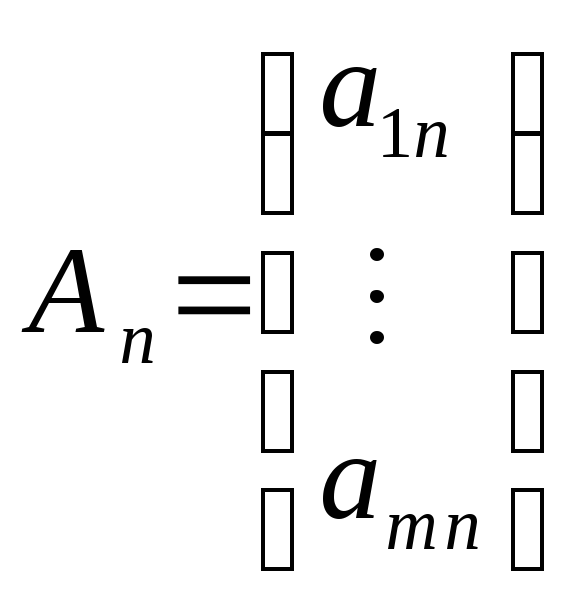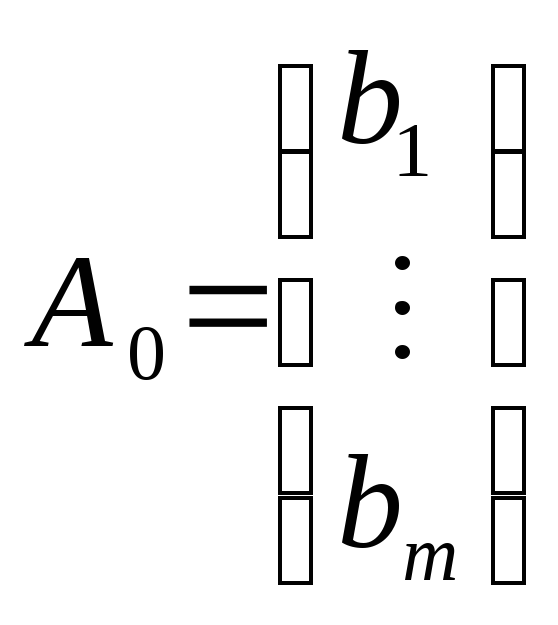,…, , (3)

Визначення. План називається опорним, якщо серед векторів векторів лінійно незалежні.

Визначення. Оптимальним називається план, що задовольняє системі (2) і мінімізує (максимізує) цільову функцію.

У реальних задачах система обмежень може містити нерівності. Тоді система обмежень має вид:

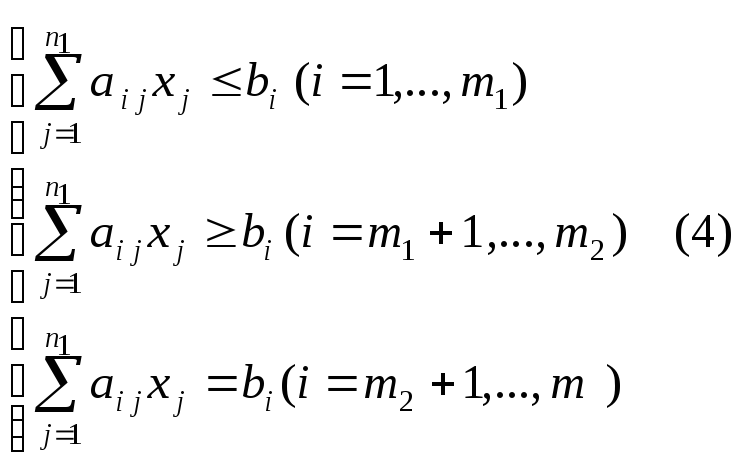
7.1.2. Геометричний метод рішення.

Цей метод використовується у випадку двох перемінних: и (на площині). Нехай потрібно мінімізувати (максимізувати) лінійну функцію: при обмеженнях:

Геометрично перші обмеження являють собою напівплощини з граничною прямою . Обмеження, що залишилися - прямі. Областю припустимих рішень є їхнє перетинання. Область припустимих рішень може являти собою замкнутий чи відкритий багатокутник, відрізок, точку і т.д. Нехай безліч припустимих рішень - обмежений замкнутий багатокутник. Лініями рівня цільової функції є набір паралельних прямих. Значення функції зростає в напрямку градієнта, убуває в напрямку антиградієнта. Будуємо лінію з нульовим рівнем: . У випадку мінімізації цільової функції будемо пересувати цю лінію паралельно самої собі в напрямку антиградієнта таким чином, щоб вона перетиналася з областю припустимих рішень. Тоді крайнє положення, що займе ця лінія, визначає точку мінімуму. При рішенні задачі максимізації нульову лінію рівня треба переміщати в напрямку градієнта.

7.1.3. Симплексний метод рішення.

Нехай потрібно мінімізувати цільову функцію при обмеженнях (4). Приведемо (4) до стандартного виду (2). Для цього до лівої частини кожного обмеження, що має вид нерівності ≤, добавляємо додатну змінну: . Якщо обмеження у виді нерівності ≥, то з лівої частини віднімаємо . Система прийме вигляд:

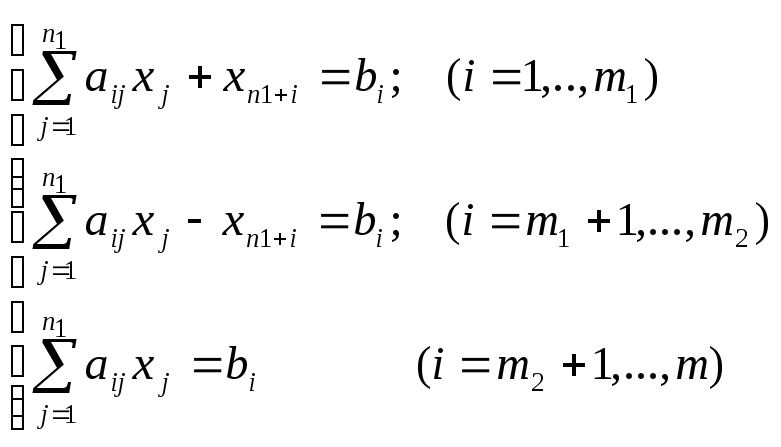
Усього змінних . Усі повинні бути додатними. Якщо , то дане рівняння потрібно помножити на (-1). Так як цільова функція не має стаціонарних точок, то своїх максимального і мінімального значень вона досягає на границі області.

Th. Нехай область припустимих рішень - обмежений замкнутий багатогранник, тоді мінімальне (максимальне) значення цільової функції досягається в кутовій точці.

Так як число невідомих більше числа рівнянь , то частина невідомих покладається базисними. Вільні змінні переносяться в праву частину. Система вирішується відносно базисних змінних. Така система сумісна, якщо визначник, що складається з коефіцієнтів при базисних невідомих у системі обмежень відмінний від нуля, чи якщо вектори , що відповідають базисним змінним, є незалежними.

Визначення. Рішення називається базисним, якщо вільні змінні рівні 0.

Кожне базисне рішення відповідає кутовій точці. Кількість базисних рішень:

Таким чином, щоб знайти оптимальне рішення, потрібно обчислити значення цільової функції у всіх кутових точках і вибрати точку, у якій значення цільової функції мінімально (максимально); якщо n велике, то кількість кутових точок велике число.

Визначення. Симплексний метод - упорядкований перехід від одного базисного рішення до іншого, при якому відбувається зменшення значення цільової функції. (Використовується для відшукання мінімального значення цільової функції )

Розглянемо побудову нульового базисного рішення. Припустимо, що система обмежень (3) містить одиничних векторів (така ситуація виникає, якщо всі обмеження визначаються нерівностями ≤; інакше перші перемінних вибираються в якості базисних і щодо них вирішується система лінійних рівнянь ). Тоді система обмежень має вигляд:

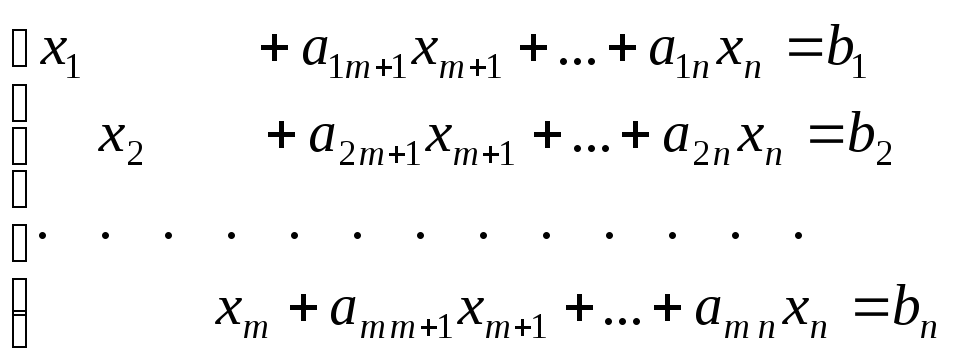
Базисні змінні: ; інші - вільні. Нехай вільні змінні рівні 0, отримуємо нульове базисне рішення: .

Далі виникає необхідність перевірити, чи не є знайдене базисне рішення оптимальним. Помітимо, що вектори системи обмежень мають вигляд:

; ;…;; ;…;.

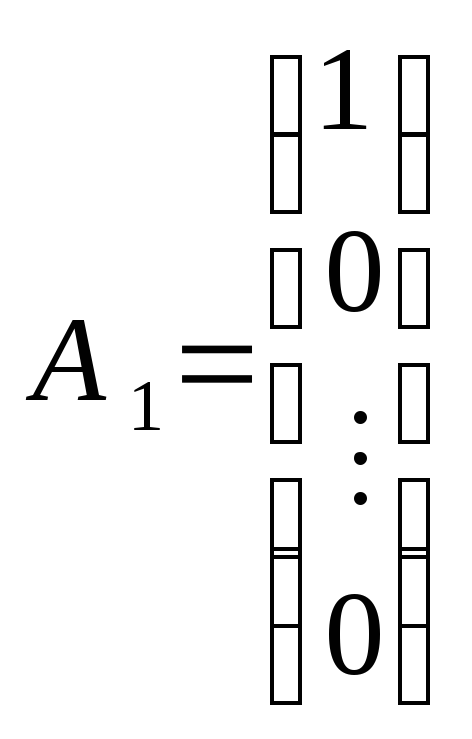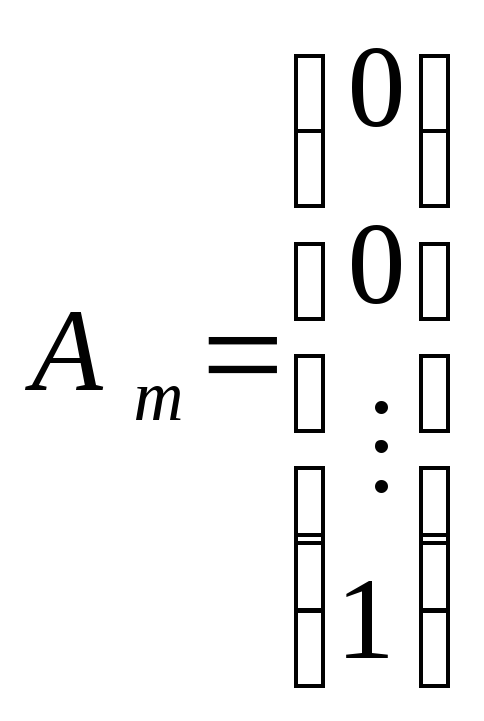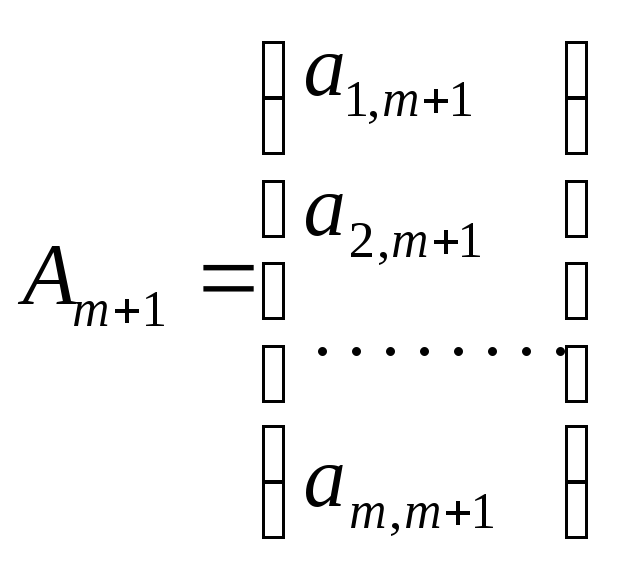Вектори ,…, – одиничні і утворюють базис у – вимірному просторі, тобто кожний з векторів можна розкласти за даним базисом:

Так як базис одиничний, то . Кожному розкладанню відповідає єдине значення :

Th: (критерій оптимальності) Якщо для деякого базисного рішення розкладання усіх векторів задовольняють умові , то план оптимальний, інакше потрібно вибрати новий базис і шукати нове базисне рішення.