
- •Питання до модульного контролю 1 з дисципліни
- •Питання до модульного контролю 2 з дисципліни
- •Текстовий редактор. Редактор формул.
- •Панель Programming
- •Панель Symbolic.
- •1.1.2. Створення й використання простих формул 7
- •1. 1.3. Абсолютні й відносні адреси чарунок 7
- •4. Лабораторна робота №4 „Основні прийоми роботи в Системе MathCad” 37
- •5.1.3. Метод ітерацій. 52
- •5.1.4. Метод Зейделя. 53
- •1.1. Теоретичні відомості
- •1.1. 1.Основні поняття електронних таблиць
- •1.1.2. Створення й використання простих формул
- •1. 1.3. Абсолютні й відносні адреси чарунок
- •Рекомендації й вимоги до виконання завдання 2
- •Питання для самоперевірки
- •2. Лабораторна робота №2 „Побудувати рівняння моделі методом найменших квадратів.”
- •2.1. Теоретичні відомості
- •2.2. Приклад виконання лабораторної роботи №2
- •2.3.Завдання до лабораторної роботи №2
- •Питання для самоперевірки
- •3.1.Теоретичні відомості .
- •3.1.1. Постановка задачі.
- •Метод Ньютона (дотичних).
- •3.2. Приклад виконання лабораторної роботи №3
- •3. 3. Завдання до лабораторної роботи №3
- •3.4. Використання Excel для развязку лабораторної роботи №3
- •Питання для самоперевірки
- •4.1. Теоретичні відомості
- •4.1.1. Призначення MathCad. Стандартний інтерфейс.
- •4.1.2. Панель інструментів Математика(Math).
- •4.1.3. Текстовий редактор.
- •4.1.4. Редактор формул.
- •4.1.6. Користувальницькі й стандартні функції.
- •4.1.7. Побудова графіків.
- •4.1.8. Робота з векторами й матрицями.
- •Обчислення визначника;
- •4.1.9. Панель Programming.
- •4.1.10. Панель Symbolic.
- •4. 2. Завдання та приклад виконання лабораторної роботи №4 Зробить завдання по наведеному зразку
- •Питання для самоперевірки
- •Використовувана література.
- •5.1. Теоретичні відомості
- •5.1.1. Норма вектора. Норма матриці.
- •5.1.2. Приведення системи до виду зручному для ітерацій.
- •5.1.3. Метод ітерацій.
- •5.1.4. Метод Зейделя.
- •5.2. Приклад виконання лабораторної роботи №5
- •5.3. Завдання до лабораторної роботи №5
- •Питання для самоперевірки
- •Використовувана література
- •6.1.Теоретичні відомості
- •6.1.1. Постановка задачі.
- •6.1.2. Інтерполяційний многочлен Лагранжа
- •6.1.2.1. Погрішність інтерполяції.
- •Інтерполяційний многочлен Лагранжа з рівновіддаленими вузлами.
- •6.1.3. Інтерполяційний многочлен Ньютона
- •6.1.3.1. Кінцеві різниці.
- •6.1.3.2. Формула Ньютона для інтерполяції «вперед».
- •6.1.3.3. Формула Ньютона для інтерполяції «назад».
- •6.2. Приклад виконання лабораторної роботи №6
- •6.3. Завдання до лабораторної роботи №6
- •Питання для самоперевірки
- •Література, що використовується
- •7. Лабораторна робота №7 „Рішення задачі лінійного програмування. ”
- •7.1. Теоретичні відомості
- •7.1.1. Постановка задачі.
- •7.1.2. Геометричний метод рішення.
- •7.1.3. Симплексний метод рішення.
- •7.1.4. Алгоритм симплексного методу.
- •7.2. Приклад виконання лабораторної роботи №7
- •Задачі лінійного програмування
- •7.3. Завдання до лабораторної роботи №7
- •Питання для самоперевірки
- •Використовувана література
- •8. Список літератури
- •Методичні вказівки до виконання лабораторних робіт з дисципліни
- •Для студентів денної форми навчання напряму підготовки
- •6.051301 „Хімічна технологія”.
- •1 Семестр.
4. 2. Завдання та приклад виконання лабораторної роботи №4 Зробить завдання по наведеному зразку

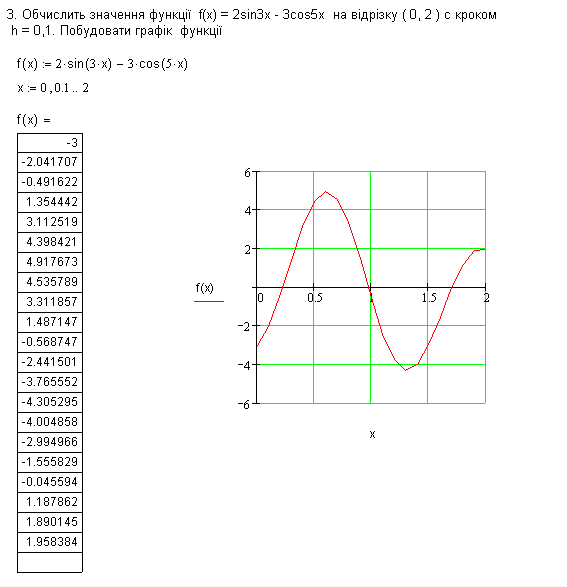
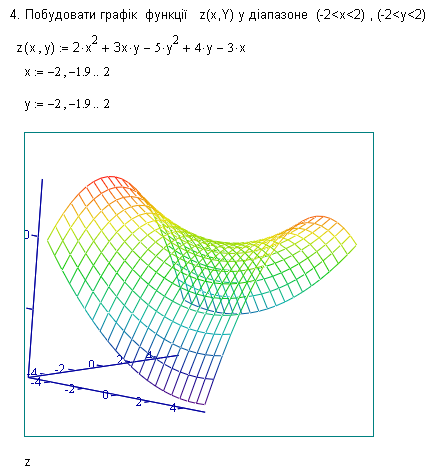
Питання для самоперевірки
-
Які елементи вікна MathCad?
-
Які палітри можна відкрити в панелі Math?
-
Як створюються текстові блоки?
-
Як уводяться формули?
-
Яким образом визначається ранжирована змінна?
-
Як увести в текст стандартну функцію?
-
Як будується графік на площині?
-
Як визначається матриця і які дії можна зробити над матрицями?
-
Які команди використовуються для побудови програмних блоків?
-
Які команди символьних перетворень можна ввести з панелі Symbolic?.
Використовувана література.
[6] стор. 55-98.
5. Лабораторна робота №5 „Пошук наближеного рішення системи рівнянь ”
Ціль роботи: вивчити наближені методи рішення системи рівнянь придбати навички рішення системи рівнянь методами ітерацій, Зейделя та з використанням системи MathCAD.
5.1. Теоретичні відомості
5.1.1. Норма вектора. Норма матриці.
Визн.
Нормою вектора називається відображення
в просторі
![]() ,
яке кожному вектору
,
яке кожному вектору
![]() ставить у відповідність число, що
позначається
ставить у відповідність число, що
позначається
![]() і задовольняє наступним властивостям.
і задовольняє наступним властивостям.
Властивості норми:
-
Норма вектора

-
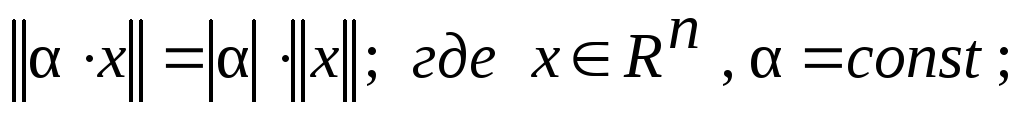
-

У
лінійному просторі
![]() - мірних векторів задамо норму двома
способами:
- мірних векторів задамо норму двома
способами:
1.
![]() 2.
2.
![]()
У
лінійному просторі квадратних
![]() - мірних матриць виду:
- мірних матриць виду:
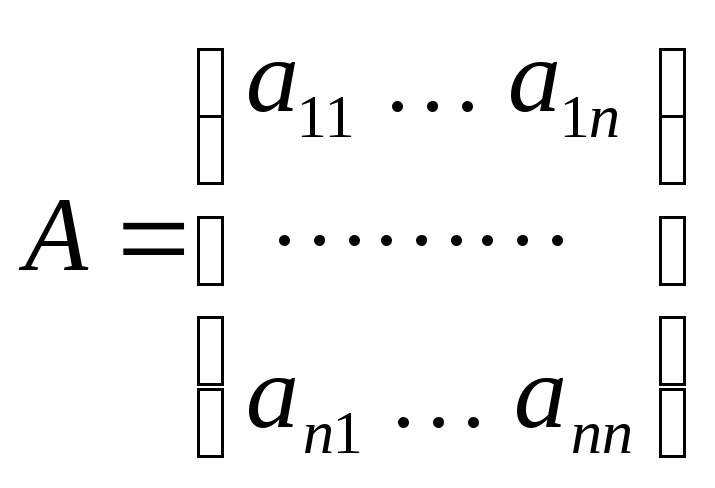 норму
визначимо в такий спосіб:
норму
визначимо в такий спосіб:
![]() ,
де
,
де
![]() - верхня грань.
- верхня грань.
Таким чином, одержуємо, що норма матриці погоджена з нормою вектора.
Будемо обчислювати норму матриці за формулами:
1.
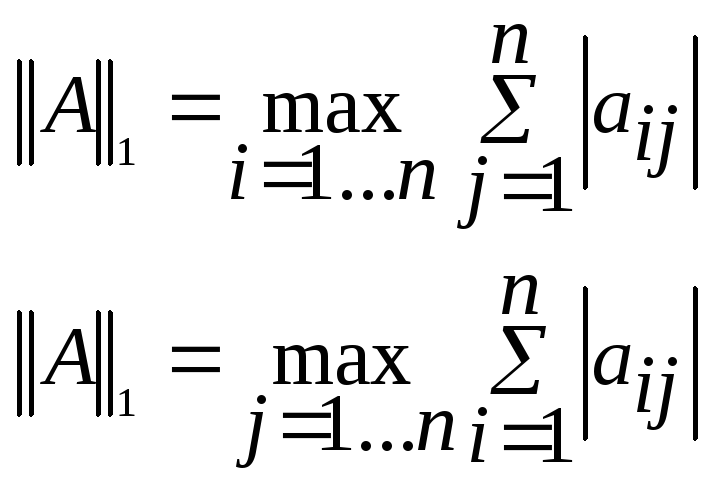 2.
2.
![]()
З визначення норми матриці випливає:
![]()
5.1.2. Приведення системи до виду зручному для ітерацій.
Розглянемо систему лінійних рівнянь:
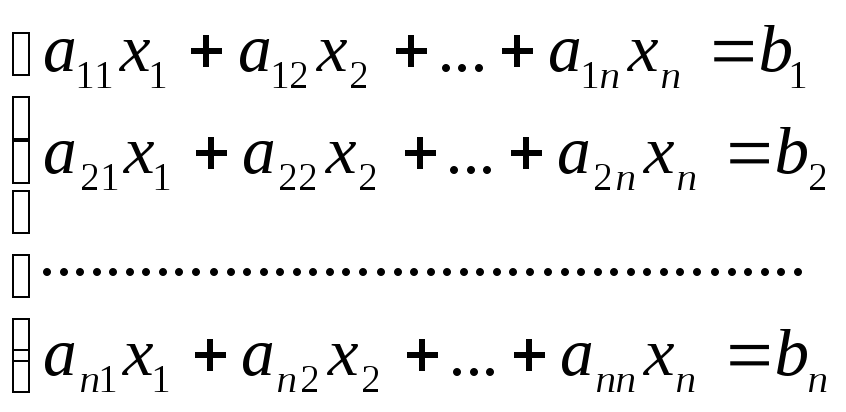
Матрична
форма запису
![]() (1)
(1)
Приведемо систему до виду, зручному для ітерацій:
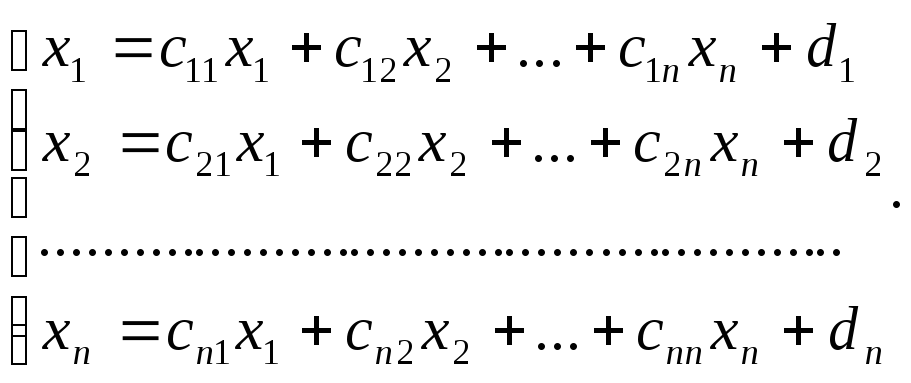
тобто
![]() (2).
(2).
Розглянемо два способи приведення системи до виду, зручному для ітерацій:
1)
У i-тому
рівнянні системи (1) усі доданки перенесемо
з лівої в праву частину, крім доданка,
що містить у собі
![]() і потім розділимо рівняння на
і потім розділимо рівняння на
![]() .
Коефіцієнти
.
Коефіцієнти
![]() визначаються за формулами:
визначаються за формулами:
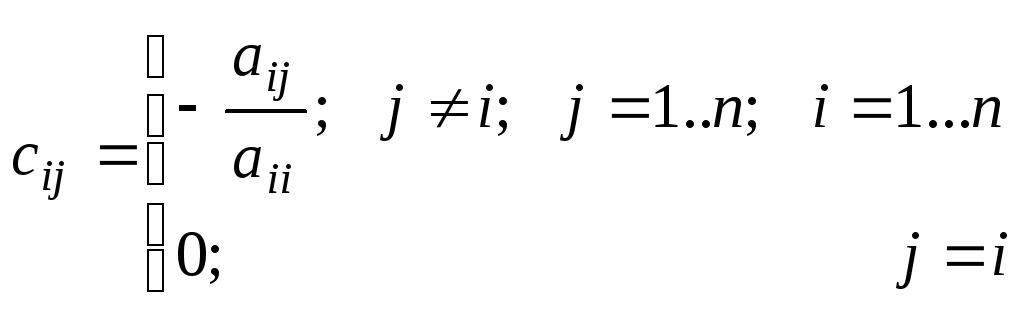
![]()
![]()
2)
Усі
доданки i-го
рівняння переносимо з лівої в праву
частину і до обох частин рівняння додамо
![]() при цьому коефіцієнти
при цьому коефіцієнти
![]() ,
,![]() визначаються за формулами:
визначаються за формулами:
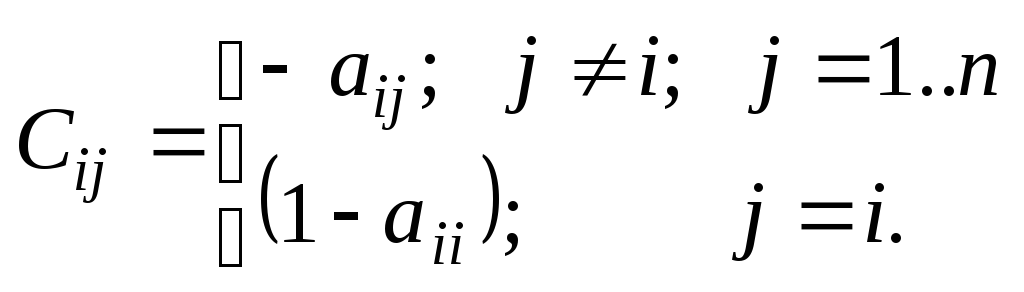 .
.
![]()
5.1.3. Метод ітерацій.
Нехай
система рівнянь приведена до виду,
зручному для ітерацій
![]() .
.
Виберемо довільним образом нульове наближення:
![]() .
Звичайно
як нульове наближення вибирається
стовпець вільних членів:
.
Звичайно
як нульове наближення вибирається
стовпець вільних членів:![]() Далі будується ітераційна послідовність
за формулою:
Далі будується ітераційна послідовність
за формулою:![]()
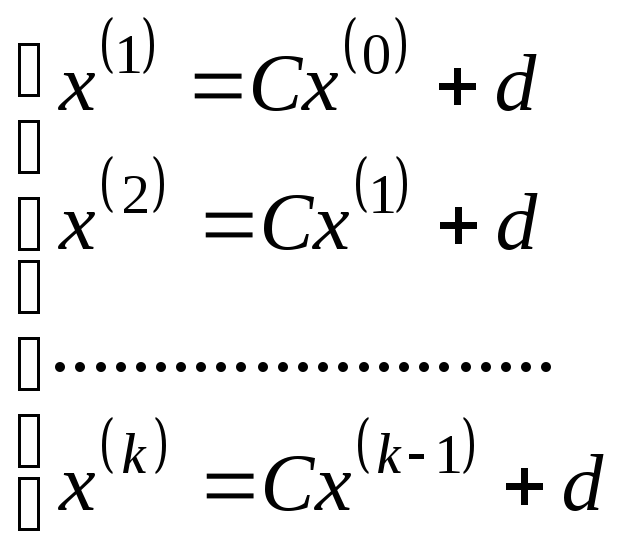 (3)
(3)
Помітимо, що i-та компонента k-го наближення обчислюється у наступний спосіб:
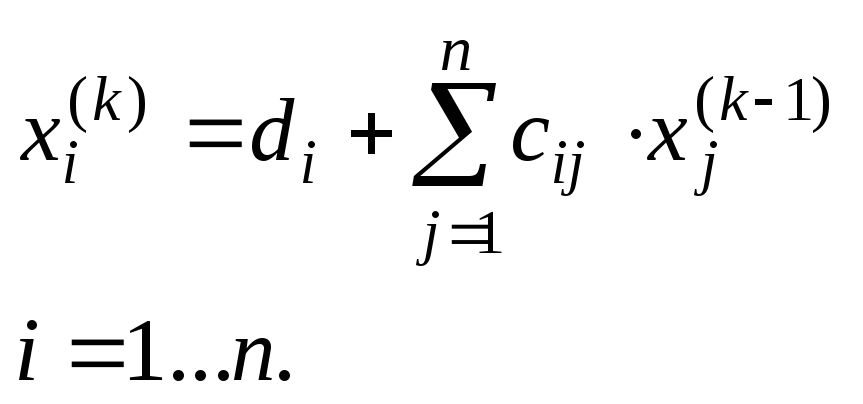 .
.
Th:
Якщо
![]() ,
то система рівнянь (2) має єдине рішення
і послідовність ітерацій (3) сходиться
до цього рішення зі швидкістю убуваючої
геометричної прогресії (без довед.).
,
то система рівнянь (2) має єдине рішення
і послідовність ітерацій (3) сходиться
до цього рішення зі швидкістю убуваючої
геометричної прогресії (без довед.).
Похибку k-ої ітерації визначається за формулою:
![]() ,
де xk
–
точне рішення.
,
де xk
–
точне рішення.
5.1.4. Метод Зейделя.
Нехай
дана система рівнянь (1) :![]() .
За допомогою першого способу приводимо
цю систему до виду, зручному для ітерацій:
.
За допомогою першого способу приводимо
цю систему до виду, зручному для ітерацій:
![]() .
Вибираємо
нульове наближення
.
Вибираємо
нульове наближення
![]() і будуємо ітераційний процес. Будемо
вважати, що значення компонентів (k-1)-го
наближення відомі, тоді компоненти k-го
наближення визначаються за формулою:
і будуємо ітераційний процес. Будемо
вважати, що значення компонентів (k-1)-го
наближення відомі, тоді компоненти k-го
наближення визначаються за формулою:

Таким чином, при обчисленні і-ої компоненти k-го наближення вже використовуються компоненти k-го наближення з номерами, що менші за і. Похибку k-го наближення визначається таким же чином, як і в методі ітерацій.
Теореми збіжності:
Th1:
Якщо
норма
![]() ,
то послідовність ітерацій, сформована
за м. Зейделя сходиться до точного
рішення, незалежно від нульового
наближення.
,
то послідовність ітерацій, сформована
за м. Зейделя сходиться до точного
рішення, незалежно від нульового
наближення.
Th2: Система (1) має єдине рішення, і послідовність ітерацій, сформована за м. Зейделя сходиться до точного рішення, якщо виконано наступну умову:
![]()
