6.1.2. Інтерполяційний многочлен Лагранжа

Визн. Інтерполяційний многочлен вигляду

;

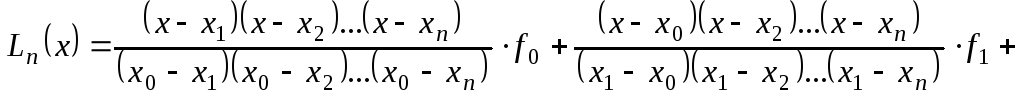
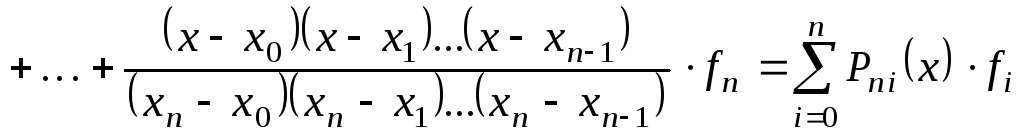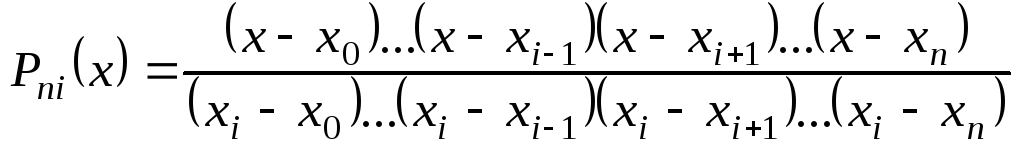
називається інтерполяційним многочленом Лагранжа.

6.1.2.1. Погрішність інтерполяції.

Хай функція n+1 раз безперервно диференційована на, де знаходяться всі вузли інтерполяції. Погрішність інтерполяції визначається за формулою:

, де

Оскільки похідна n+1-го порядку безперервна на, то вона обмежена, отже, існує таке число , що справедливо .

Погрішність інтерполяції в точці оцінюється за формулою:

; . (3)

Максимальна погрішність інтерполяції визначається таким чином:

. (4)

2. Інтерполяційний многочлен Лагранжа з рівновіддаленими вузлами.

Хай відомі значення функції в рівновіддалених точках з кроком h>0: ; .

Введемо поняття фази інтерполяції : ; . Фаза – безрозмірна величина, не залежна від .

Виразимо : Запишемо через фазу многочлен

, де.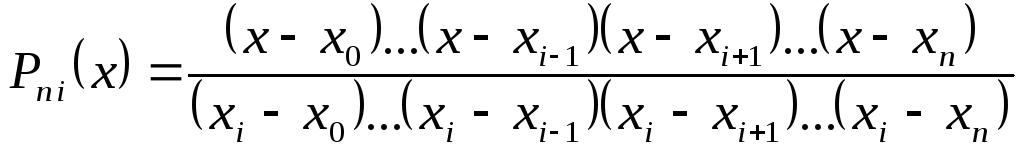

Помітимо, що ;

.

Підставляємо відповідні вирази в .

.

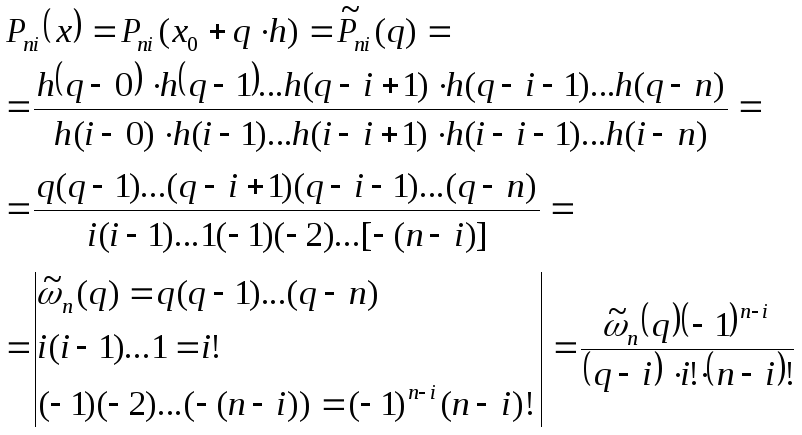
Погрішність інтерполяції в точці рівна

Максимальна погрішність інтерполяції:

.

Погрішність в точці :

де .

6.1.3. Інтерполяційний многочлен Ньютона

6.1.3.1. Кінцеві різниці.

Введемо поняття кінцевої різниці. Хай відомі значення функції в точках , причому .

Визн. Величина називається кінцевою різницею 1-го порядку функції в точці з кроком . (Наприклад: ) .

Визн. Величина називається кінцевою різницею 2-го порядку функції в точці з кроком . (Наприклад: ) .

Визн. Кінцева різниця n-го порядку функції в точці визначається за рекуррентною формулою:

.

Кінцеві різниці зручно записувати у вигляді таблиці:

6.1.3.2. Формула Ньютона для інтерполяції «вперед».

Хай відомі значення функції в точках

, причому .

Розглянемо інтерполяційний многочлен у вигляді:

Коефіцієнти визначимо з умови (1) для інтерполяційних многочленів : .

1. Хай ;.

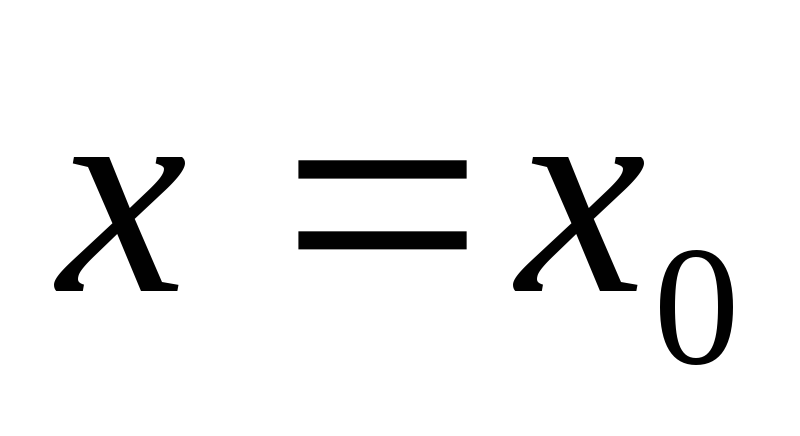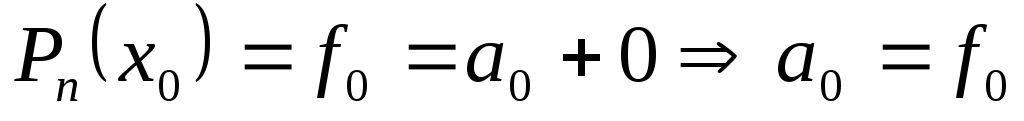2. Хай ;

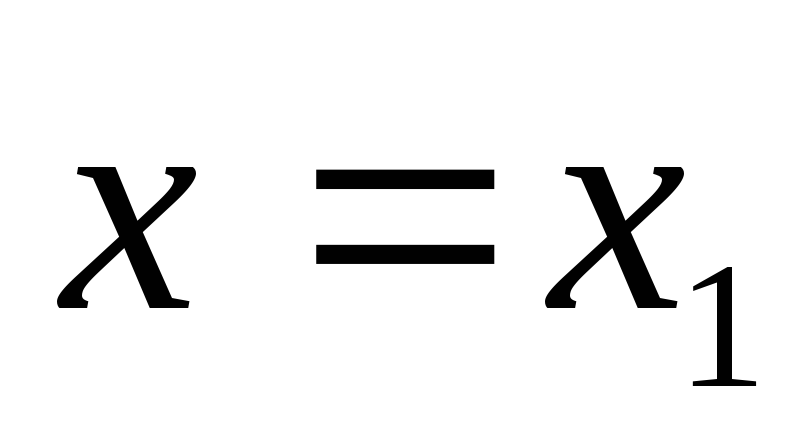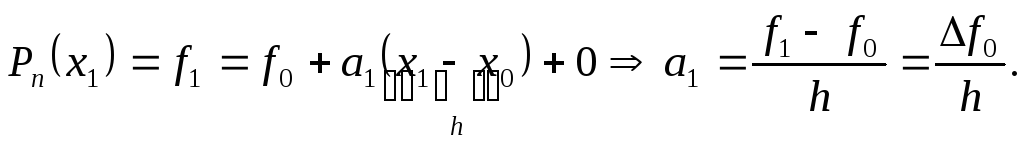
І так далі, останній коефіцієнт: .

Підставляючи коефіцієнти в, отримаємо многочлен:

Отриманий многочлен називається першою інтерполяційною формулою Ньютона або інтерполяційним многочленом Ньютона для інтерполяції “вперед”.

Перейдемо до фази інтерполяції:

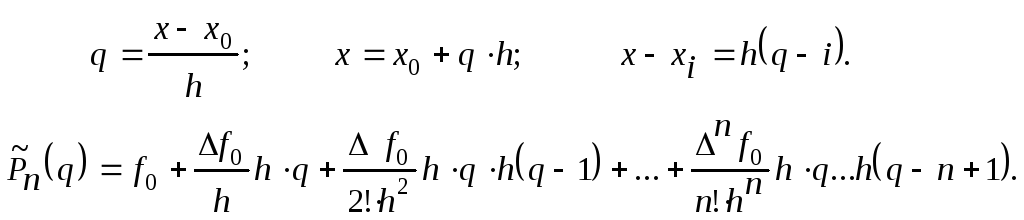Многочлен Ньютона від змінної q має вигляд:

6.1.3.3. Формула Ньютона для інтерполяції «назад».

У виведеній формулі за початок відліку вибиралася точка Виберемо за початок відліку точку і шукатимемо інтерполяційний многочлен у вигляді:

1. Хай ;

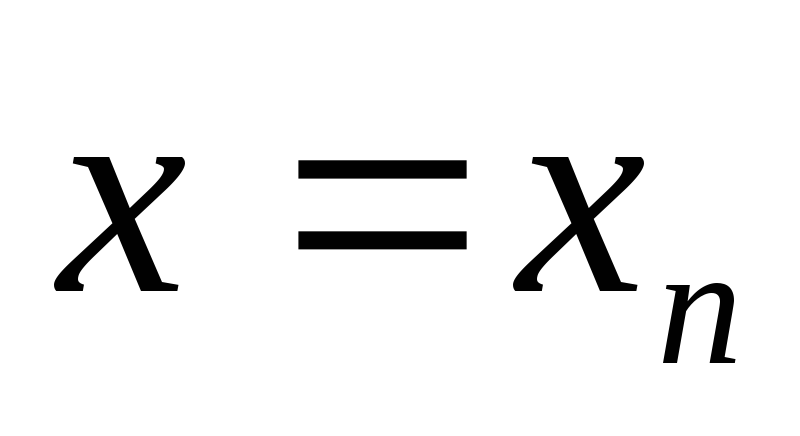2. Хай;

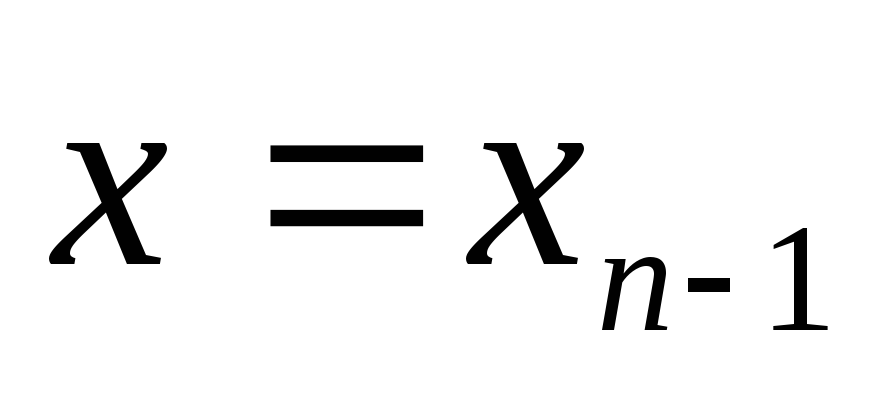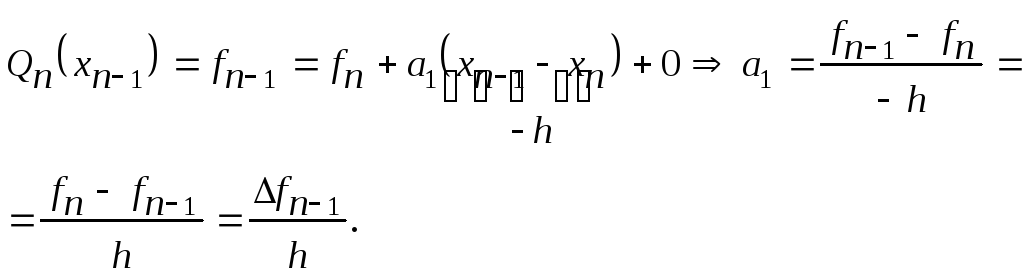
І так далі, останній коефіцієнт: .

Підставляючи знайдені коефіцієнти, отримаємо :

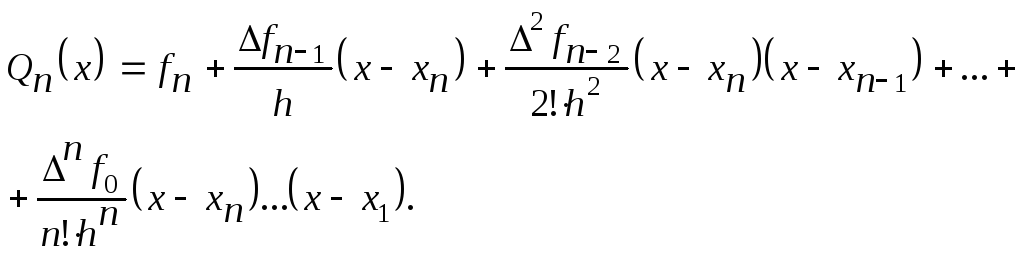
Отримана формула називається другою інтерполяційною формулою Ньютона або інтерполяційним многочленом Ньютона для інтерполяції “назад”.

Отримаємо формулу для інтерполяції ”назад через” фазу. Задамо фазу таким чином :

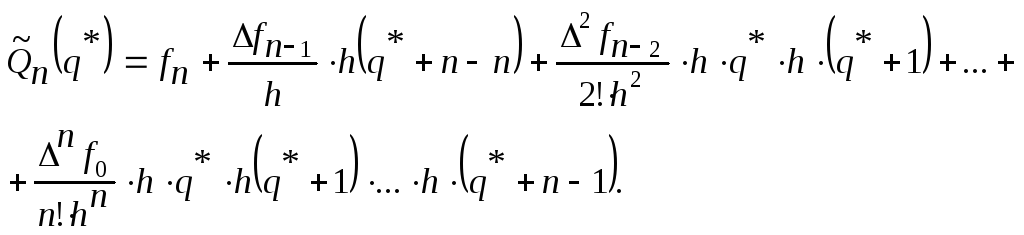
Формула Ньютона для інтерполяції “назад через” фазу має вигляд:

Зауваження: Недоліком многочлена Лагранжа є те, що при додаванні хоча б однієї точки інтерполяції, необхідно перерахувати все P_ni(x). Для многочлена Ньютона додавання точки приводить до додавання одного доданку без перерахунку попередніх.