Р ис 3.11. Пересекающиеся прямые. Р ис. 3.12. Параллельные прямые.

Скрещивающиеся прямые не имеют общей точки, а точки пересечения их одноименных проекций не лежат на одной линии связи (рис. 3.13).

Исключение составляет случай, когда одна из скрещивающихся прямых профильная, и для оценки взаимного положения требуется построение проекции на плоскость ₃. В данном примере BE и AC скрещиваются. Точки пересечения проекций скрещивающихся прямых лежащие на одной линии связи называются конкурирующими. По конкурирующим точкам определяется видимость элементов прямых на соответствующих плоскостях проекций.

Р ис. 3.13. Скрещивающиеся прямые.

Видимость точек 1 и 2 на горизонтальной плоскости проекций определяется по фронтальной проекции, какая из точек по линии связи расположена выше (указано стрелкой). В данном случае точка 1, принадлежащая прямой а видима на ₁.

Видимость точек 3 и 4 на фронтальной плоскости проекций определяется по горизонтальной проекции, какая из точек по линии связи расположена ближе к наблюдателю (указано стрелкой). В данном случае точка 3, принадлежащая прямой b видима.

Вопросы и задачи для самоконтроля

Когда след прямой будет находиться в бесконечно удаленной, несобственной точке?

Для какой прямой на эпюре следы:

1. лежат на оси проекций;

2. совпадают.

Построить следы прямой, определяемой точками А и В:

1. А (10, 20, 50); В (20, 50, 10).

2. А (60, 25, 60); В (20, 10, 25).

3. А (10, 15, 50); В (50, 15, 10).

Глава 4. Плоскость

4.1 Способы задания плоскости

Плоскость считается заданной; если из всех точек пространства можно выделить только те точки, которые принадлежат данной плоскости. Плоскость на чертеже может быть определена следующими способами (каждый из способов допускает переход к любому другому способу).

1. Тремя точками, не лежащими на одной прямой (рис. 4.1а).

2. Прямой и точкой вне прямой (рис. 4.1б).

3. Двумя пересекающимися прямыми (рис. 4.1в).

4. Двумя параллельными прямыми (рис. 4.1г).

5. Любой плоской фигурой-отсеком пространства (рис. 4.1д).

Р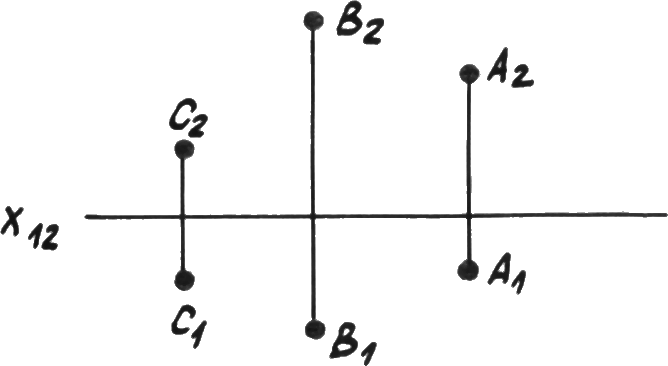 ис. 4.1а. Три точки.

Р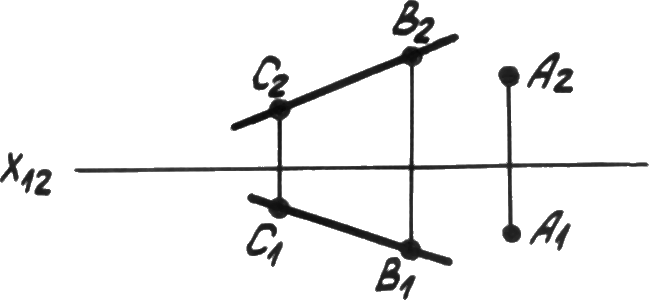 ис. 4.1б. Прямая и точка.

Р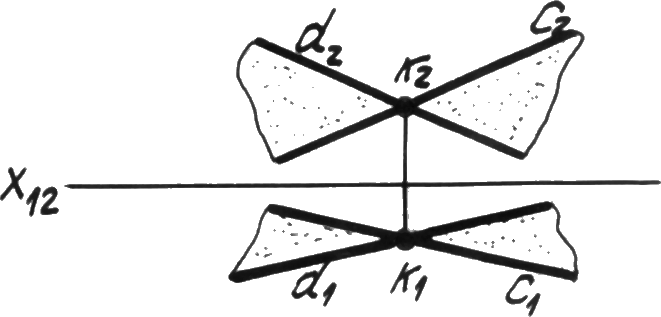 ис. 4.1в. Пересекающиеся прямые.

Р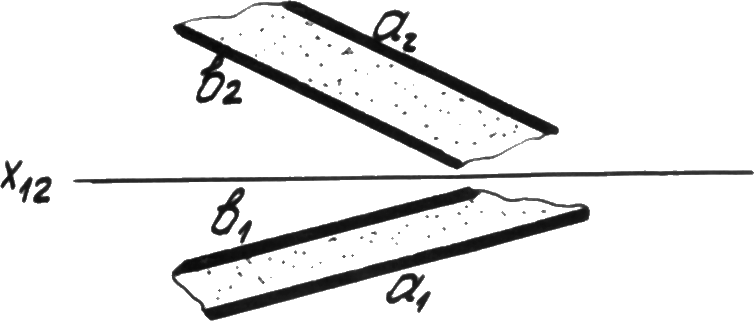 ис. 4.1г. Параллельные прямые.

Р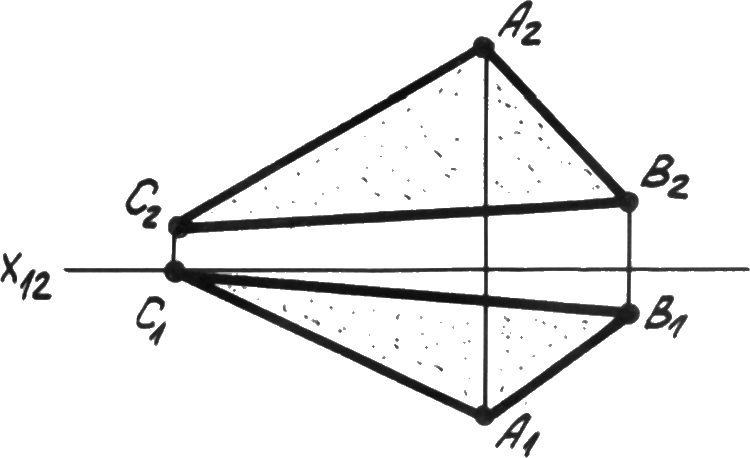 ис. 4.1д. Фигура.

6. Следами плоскости (рис. 4.2).

Следы плоскости - это линии пересечения плоскости с плоскостями проекций.

Линия пересечения плоскости с плоскостью ₁ называется горизонтальным следом плоскости Q₁, с плоскостью ₂-фронтальным следом Q₂, с плоскостью ₃-профильным следом Q₃. Точки пересечения следов на осях проекций называются точками схода следов Q_x, Q_y, Q_z.

Отрезки OQ_x , OQ_y , OQ_z, отсекаемые осями проекций, называют параметрами плоскости (рис. 4.2).

Р ис. 4.2. Следы плоскости.

4.2 Плоскости частного положения

Плоскости относительно плоскостей проекций могут быть общего и частного положения. Плоскости частного положения - это плоскости перпендикулярные или параллельные какой-либо плоскости проекций.

Плоскости перпендикулярные одной из плоскостей проекций, называются проецирующими.

1. Горизонтально проецирующая плоскость перпендикулярна горизонтальной плоскости проекций ₁ (рис. 4.3а).