Р ис. 3.4. Фронталь.

Все точки фронтали одинаково удалены от плоскости ₂, т.е. у_A =  у_B =  const. Горизонтальная проекция фронтали параллельна оси х₁₂ (A₁B₁ ||  x₁₂), профильная параллельна оси z (A₃B₃ ||  z₂₃). На плоскость ₂ фронталь проецируется без искажения, т.е. фронтальная проекция фронтали A₂B₂ является натуральной величиной, углы наклона фронтали к плоскостям ₁ и ₃ проецируются без искажения ( и ).

3. Прямые параллельные плоскости ₃ называются профильными (рис. 3.5).

Р ис. 3.5. Профильная прямая.

Все точки профильной прямой одинаково удалены от плоскости ₃, т.е. х_A =  х_B =  const. Горизонтальная и фронтальная проекции профильной прямой перпендикулярны оси х₁₂ (или параллельны соответственно осям у и z).

На плоскость ₃ профильная проекция проецируется без искажения, т.е. профильная проекция профильной прямой A₃B₃ является натуральной величиной. Углы наклона прямой AB к плоскостям ₁ и ₂ проецируются без искажения ( и ).

Таким образом, прямые линии уровня проецируются без искажения на ту плоскость проекций, которая прямая параллельна.

Рассмотрим проецирующие прямые (рис. 3.6 - 3.8).

Р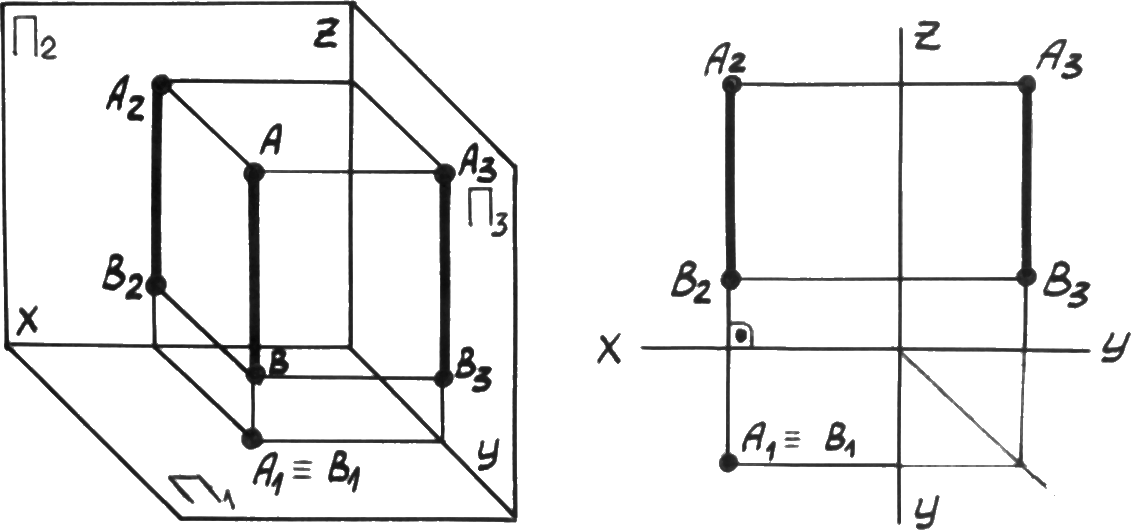 ис. 3.6. Горизонтально проецирующая прямая.

Р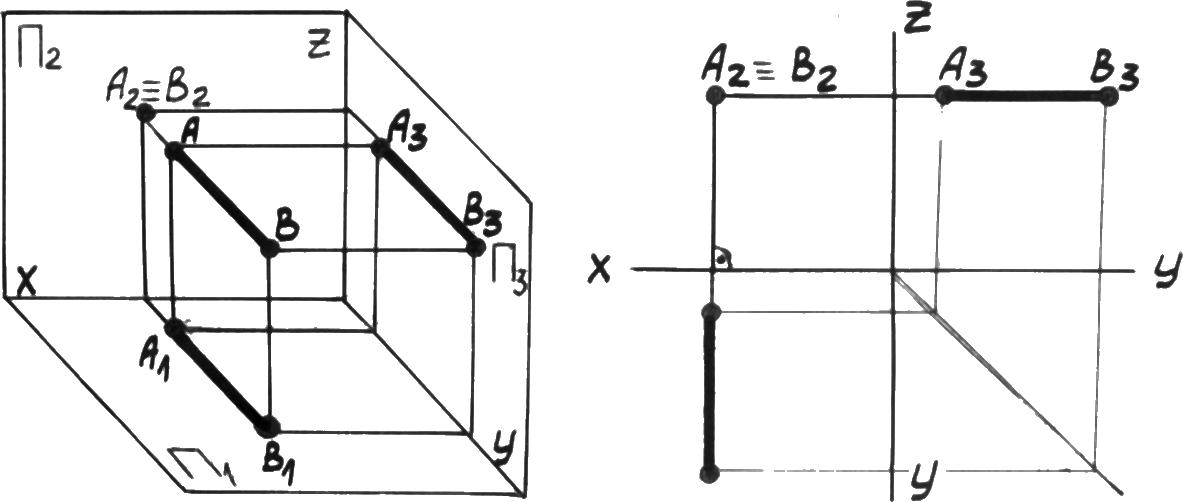 ис. 3.7. Фронтально проецирующая прямая.

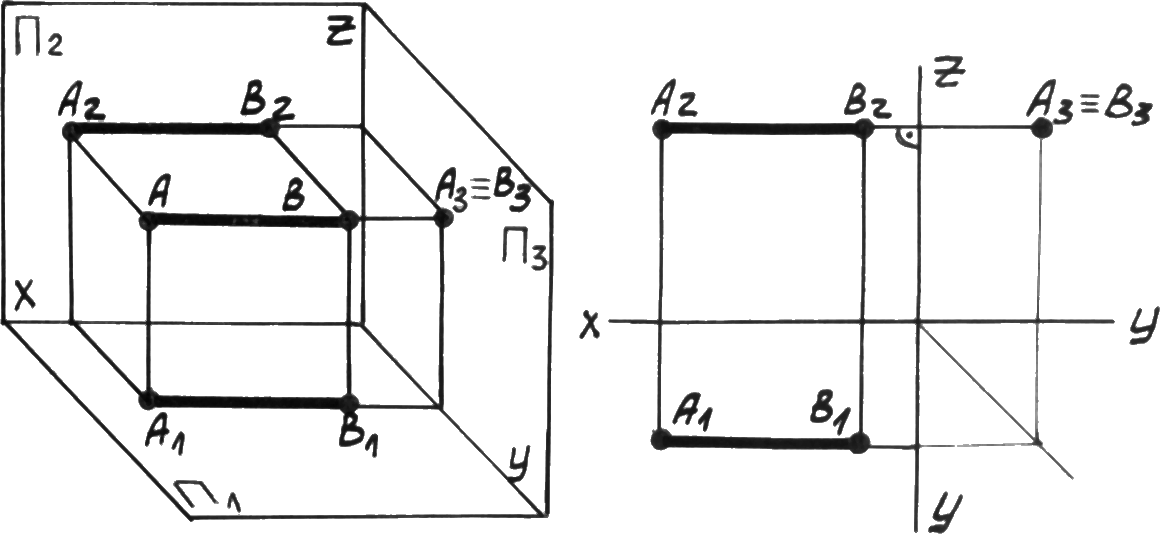Р ис. 3.8. Профильно проецирующая прямая.

Для проецирующих прямых характерно, что проекция прямой на ту плоскость, которой прямая перпендикулярна, обращается в точку. Две другие проекции проецирующих прямых перпендикулярны осям. Проецирующие прямые называются горизонтально проецирующая ( ₁), рис. 3.6; фронтально проецирующая ( ₂), рис. 3.7; профильно проецирующая ( ₃), рис. 3.8.

3.3 Определение длины отрезка прямой и углов ее наклона. к плоскостям проекций (способ прямоугольного треугольника)

Прямая линия общего положения составляет с плоскостями проекций произвольные углы. Отрезок прямой общего положения проецируется на плоскости проекций с искажениями. Рассмотрим задачу на определение длины отрезка прямой и углов ее наклона к плоскостям проекций.

В пространстве отрезок АВ прямой общего положения отнесенный к двум плоскостям проекций представляет собой гипотезу двух прямоугольных треугольников АВС и АВD (рис. 3.9а).

Одним катетом треугольников является одна из проекций отрезка, другим разность недостающих координат. Угол между гипотенузой (отрезком АВ) и катетом (проекцией) есть угол наклона прямой к соответствующей плоскости проекций.

В треугольнике АВС катет АС =  А₁В₁, катет ВС =  z_AB,  – угол наклона отрезка АВ к плоскости ₁. z_AB =  (z_A - z_B) – разность координат точек А и В до плоскости ₁.

В треугольнике АВD катет BD =  А₂В₂, катет AD =  y_AB,  – угол наклона отрезка АВ к плоскости ₂. y_AB =  (y_A - y_B) – разность координат точек А и В до плоскости ₂. На эпюре (рис. 3.9б) легко построить треугольники равные рассмотренным.

Р ис. 3.9а. Отрезок в пространстве. Р ис3.9б. Определение длины отрезка прямой и углов ее наклона к плоскостям проекций.

Например, к проекции А₁В₁, как к катету прямоугольного треугольника, достраиваем от любой из точек (в нашем случае В₁), второй катет, равный разности недостающих координат точек отрезка В₁В₀ =  z_AB. Разность координат z точек А и В измеряется на фронтальной проекции. Гипотенуза А₁В₀ прямоугольного треугольника А₁В₁В₀ является натуральной величиной отрезка АВ, а угол  между проекцией и гипотенузой – это угол наклона отрезка прямой к плоскости ₁.

Аналогичные построения выполним на фронтальной проекции для определения угла наклона к плоскости ₂.