Р ис. 5.10. Способ плоскопараллельного перемещения.

Проекция АВ является натуральной величиной АВ, т.к. первым перемещение прямая преобразована во фронталь.

Второе перемещение выполним параллельно плоскости ₂. Фронтальную проекцию переместим без изменений размеров перпендикулярно оси x(АВ  x). На горизонтальной проекции точки движутся параллельно оси x, и отрезок АВ преобразуется в горизонтально проецирующую прямую.

Задача: Определить расстояние от точки S до плоскости АВС (рис. 5.11) способом плоскопараллельного перемещения.

Решение: Для решения задачи необходимо преобразовать плоскость общего положения в проецирующую. Если одна из проекций плоскости будет преобразована в прямую линию, то можно отпустить перпендикуляр из точки S и определить расстояние. Перемещаем плоскость АВС перпендикулярно плоскости ₂.

Р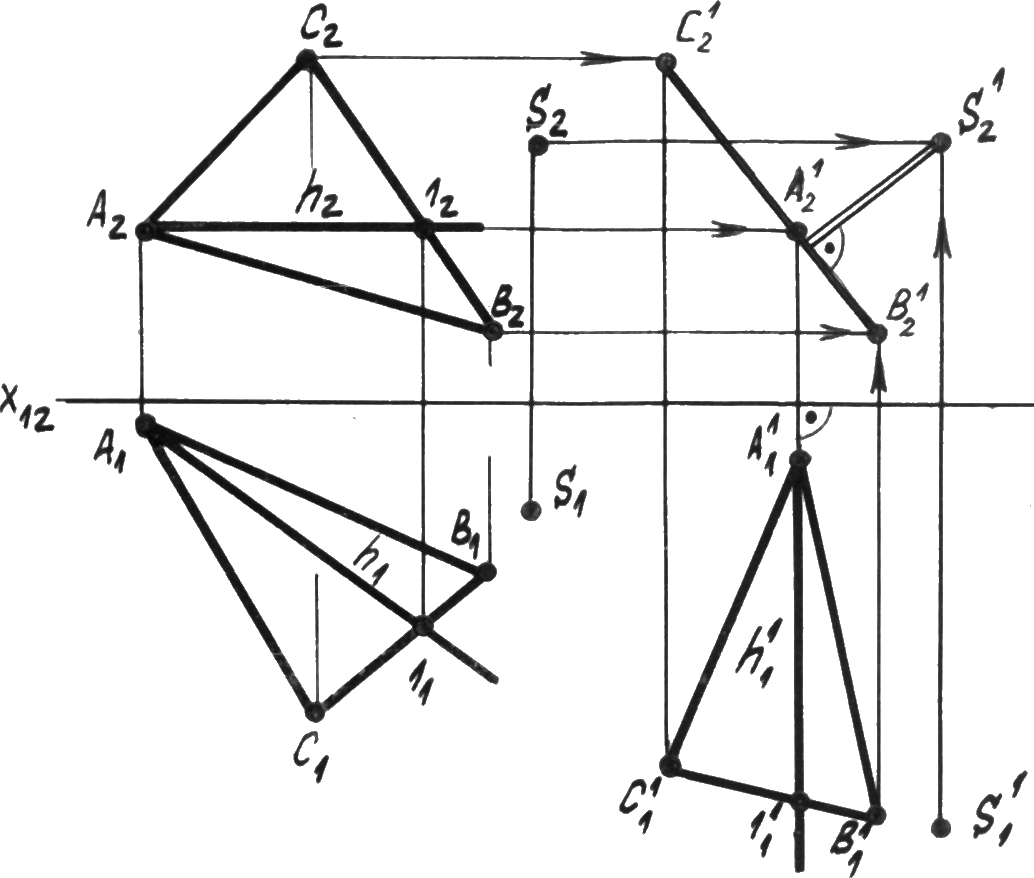 ис. 5.11.

Располагаем новую горизонтальную проекцию прямоугольника АВС без изменения формы и размера так, чтобы горизонталь h оказалась перпендикулярно плоскости ₂. На фронтальной проекции точки перемещаются параллельно оси x, Новая фронтальная проекция треугольника АВС преобразуется в прямую линию. Опускаем перпендикуляр из перемещенной точки S на новую фронтальную проекцию треугольника.

Вопросы и задачи для самоконтроля

1. В чём сущность способа перемещения плоскостей проекций?

2. Сколько нужно выполнить последовательных преобразований и каких, чтобы определить натуральную величину плоскости общего положения?

3. Как движутся точки геометрического объекта при его вращении вокруг осей перпендикулярных плоскостям проекции?

4. Сколько нужно выполнить последовательных вращений и каких, чтобы преобразовать прямую общего положения в проецирующую?

5. Определите расстояние между двумя параллельными прямыми общего положения способом плоскопараллельного перемещения?

6. Определите натуральную величину треугольника вращением вокруг фронтали.

Глава 6. Поверхности

6.1. Многогранные поверхности

6.1.1. Классификация многогранников

Многогранник - это замкнутая пространственная фигура, ограниченная плоскими многоугольниками (частями пересекающихся плоскостей).

Выпуклые многоугольники - это такие у которых все вершины и ребра находятся по одну сторону любой из их граней.

Наибольший интерес представляют призмы, пирамиды и правильные выпуклые многоугольники - тела Платона.

Призма - многоугольник, две грани которого представляют собой равные многоугольники (основания призмы) со взаимно параллельными сторонами, все другие грани- параллелограммы (или прямоугольники).

Пирамида - многогранник, одна грань которого - многоугольник, а остальные грани треугольники с общей вершиной.

Тела Платона - многогранники, все грани которых представляют собой правильные и равные многоугольники. Углы при вершинах таких многоугольников равны между собой. Существует 5 типов правильных многогранников: гексаэдр (куб)- 6 квадратов, тетраэдр, октаэдр, икосаэдр - 4, 8, 20 правильных треугольников, додекаэдр - 12 правильных пятиугольников.

6.1.2. Некоторые позиционные задачи пересечения многогранника с прямой и плоскостью

Плоскость пересекает многогранную поверхность по плоской замкнутой ломаной линии, называемой фигурой сечения. Вершины и стороны фигуры сечения определяются пересечением заданной плоскости соответственно с рёбрами и гранями многоугольника. То есть многократно решается задача или на пересечение двух плоскостей (граней многогранника с секущей плоскостью), или на пересечение прямой с плоскостью (рёбер многогранника с секущей плоскостью). Это уже известные задачи.

Задача: Дана треугольная наклонная пирамида и секущая фронтально проецирующая плоскость  (рис. 6.1). Определить проекции фигуры сечения.

Р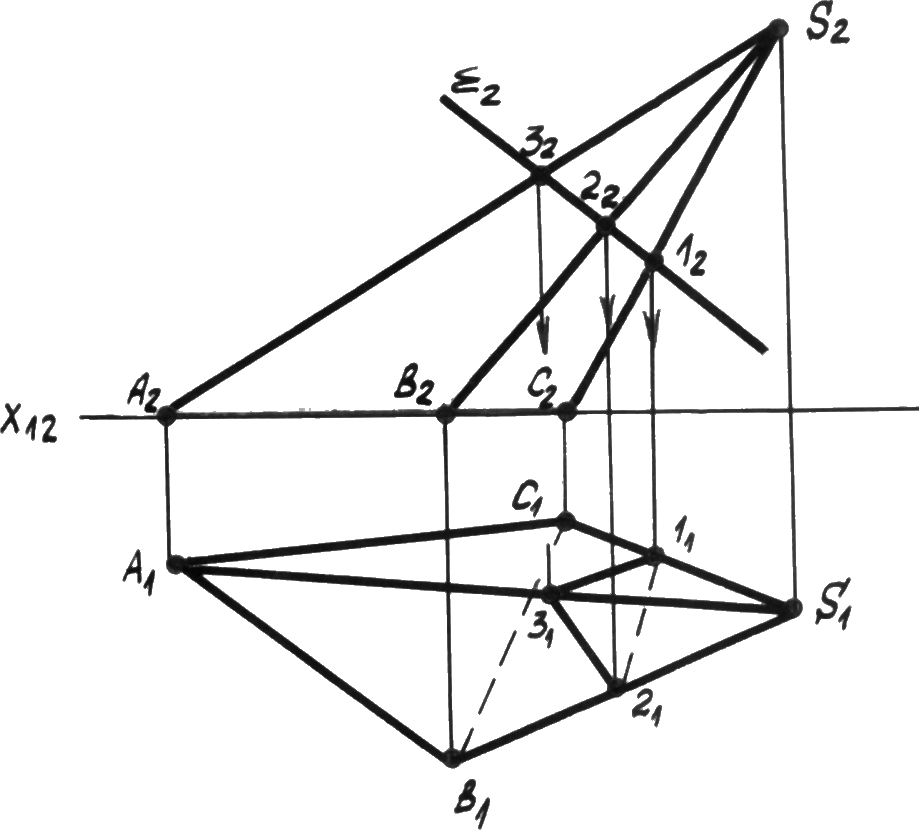 ис. 6.1.

Решение: Так как секущая плоскость является фронтально проецирующей, то фронтальная проекция фигуры сечения (1₂2₂3₂) совпадет со следом плоскости ₂. Фигура сечения является треугольником и определяется на пересечении следа плоскости с соответствующими ребрами пирамиды. По линиям связи определяем горизонтальные проекции вершин треугольника (1₁2₁3₁) на соответствующих ребрах пирамиды. Далее определяется видимость звеньев линии сечения в зависимости от видимости граней пирамиды на горизонтальной проекции.

Задача: Дана прямая треугольная призма и секущая плоскость общего положения Т (рис. 6.2). Определить проекции фигуры сечения.