3.3.4. Взаимное расположение прямой и плоскости

Прямая может принадлежать плоскости, быть ей параллельной или пересекать плоскость. Прямая принадлежит плоскости, если две точки, принадлежащие прямой и плоскости, имеют одинаковые отметки. Следствие, вытекающее из сказанного: точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости.

Прямая параллельна плоскости, если она параллельна прямой, лежащей в этой плоскости.

Прямая, пересекающая плоскость. Чтобы найти точку пересечения прямой с плоскостью, необходимо (рис. 3.28):

1) через заданную прямую m провести вспомогательную плоскость Т;

2) построить линию n пересечения заданной плоскости Σ с вспомогательной плоскостью Т;

3) отметить точку пересечения R, заданной прямой m с линией пересечения n.

Рис. 3.28

Рассмотрим задачу (рис. 3.29).Прямая m задана на плане точкой А₆ и углом наклона 35°. Через эту прямую проведена вспомогательная вертикальная плоскость Т, которая пересекает плоскость Σ по линии n (В₂ С₃ ). Таким образом, переходят от взаимного положения прямой и плоскости к взаимному положению двух прямых, лежащих в одной вертикальной плоскости. Такая задача решается построением профилей этих прямых. Пересечение прямых m и n на профиле определяет искомую точку R. Высотную отметку точки R определяют по шкале вертикальных масштабов.

Прямая, перпендикулярная плоскости. Прямая линия перпендикулярна к плоскости, если она перпендикулярна к любым двум пересекающимся прямым этой плоскости. На рис 3.30 изображена прямая m, перпендикулярная к плоскости Σ и пересекающая ее в точке А. На плане проекции прямой m и горизонтали плоскости взаимно перпендикулярны (прямой угол, одна сторона которого параллельна плоскости проекций, проецируется без искажения. Обе прямые лежат в одной вертикальной плоскости, следовательно заложения у таких прямых обратны по величине друг другу: l ^m = l /l ^u. Но l ^uΣ = l ^Σ , тогда l ^m = l / l ^Σ, то есть заложение прямой m обратно пропорционально заложению плоскости. Падения у прямой и плоскости направлены в разные стороны.

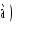
Рис. 3.29

Рис. 3.30

3.4. Проекции с числовыми отметками. Поверхности

3.4.1.Многогранники и кривые поверхности. Топографическая поверхность

В природе многие вещества имеют кристаллическое строение в виде многогранников. Многогранником называют совокупность плоских многоугольников, не лежащих в одной и той же плоскости, где каждая сторона одного из них является одновременно стороной другого. При изображении многогранника достаточно указать проекции его вершин, соединив их в определенном порядке прямыми линиями - проекциями ребер. При этом на чертеже необходимо указывать видимые и невидимые ребра. На рис. 3.31 изображены призма и пирамида, а также нахождение отметок точек, принадлежащих данным поверхностям.

Рис. 3.31

Особой группой выпуклых многоугольников является группа правильных многоугольников, у которых все грани - равные между собой правильные многоугольники и все многоугольные углы равны. Существует пять видов правильных многоугольников.

Рис. 3.32

Тетраэдр - правильный четырехугольник, ограниченный равносторонними треугольниками, имеет 4 вершины и 6 ребер (рис. 3.32 а).

Гексаэдр - правильный шестигранник (куб) - 8 вершин, 12 ребер (рис. 3.32б).

Октаэдр - правильный восьмигранник, ограниченный восемью равносторонними треугольниками - 6 вершин, 12 ребер (рис. 3.32в).

Додекаэдр - правильный двенадцатигранник, ограниченный двенадцатью правильными пятиугольниками, соединенными по три около каждой вершины.

Имеет 20 вершин и 30 ребер (рис.3.32 г).

Икосаэдр - правильный двадцатигранник, ограниченный двадцатью равносторонними треугольниками, соединенными по пяти около каждой вершины.12 вершин и 30 ребер (рис. 3.32 д).

При построении точки , лежащей на грани многогранника, необходимо провести прямую, принадлежащую этой грани и на ее проекции отметить проекцию точки.

Конические поверхности образуются перемещением прямолинейной образующей по криволинейной направляющей так, что во всех положениях образующая проходит через неподвижную точку -вершину поверхности. Конические поверхности общего вида на плане изображают направляющей горизонталью и вершиной. На рис. 3.33 показано нахождение отметки точки на поверхности конической поверхности.

Рис. 3.33

Прямой круговой конус изображается серией концентрических окружностей, проведенных через равные интервалы (рис.3.34а). Эллиптический конус с круговым основанием - серией эксцентрических окружностей (рис. 3.34 б)

Рис. 3.34

Сферические поверхности. Сферическую поверхность относят к поверхностям вращения. Она образуется вращением окружности вокруг ее диаметра. На плане сферическая поверхность определена центром К и проекцией одной из ее горизонталей (экватором сферы) (рис. 3.35).

Рис. 3.35

Топографическая поверхность. Топографическую поверхность относят к геометрически неправильным поверхностям, так как она не имеет геометрического закона образования. Для характеристики поверхности определяют положение ее характерных точек относительно плоскости проекций. На рис. 3.3 б а дан пример участка топографической поверхности, на котором показаны проекции ее отдельных точек. Такой план хотя и дает возможность составить представление о форме изображаемой поверхности, однако отличается малой наглядностью. Чтобы придать чертежу большую наглядность и облегчить тем самым его чтение, проекции точек с одинаковыми отметками соединяют плавными кривыми линиями, которые называют горизонталями (изолиниями) (рис. 3.36 б).

Рис. 3.36

Горизонтали топографической поверхности иногда определяют и как линии пересечения этой поверхности с горизонтальными плоскостями, отстоящими друг от друга на одно и то же расстояние (рис. 3.37). Разность отметок у двух смежных горизонталей называют высотой сечения.

Изображение топографической поверхности тем точнее, чем меньше разность отметок у двух смежных горизонталей. На планах горизонтали замыкаются в пределах чертежа или вне его. На более крутых склонах поверхности проекции горизонталей сближаются, на пологих – их проекции расходятся.

Рис. 3.37

Кратчайшее расстояние между проекциями двух смежных горизонталей на плане называют заложением. На рис. 3.38 через точку А топографической поверхности проведено несколько отрезков прямых АВ, АС и АD. Все они имеют разные углы падения. Наибольший угол падения имеет отрезок АС, заложение которого имеет минимальное значение. Поэтому он и будет являться проекцией линии падения поверхности в данном месте.

Рис. 3.38

На рис. 3.39 приводится пример построения проекции линии падения через заданную точку А. Из точки А₁₀₀ , как из центра, проводят дугу окружности, касающуюся ближайшей горизонтали в точке В₉₀. Точка В₉₀ , лежащая на горизонтали h₉₀ , будет принадлежать линии падения. Из точки В₉₀ проводят дугу, касающуюся следующей горизонтали в точке С₈₀ , и т. д. Из чертежа видно, что линией падения топографической поверхности является ломаная линия, каждое звено которой перпендикулярно к горизонтали, проходящей через нижний, имеющий меньшую отметку, конец звена.

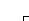
Рис. 3.39