5.2 Моделі стохастичних систем

Модель системи можна вважати детермінованою, якщо прийняти, що випадкові флуктуації значень входів, виходів і станів систем, що моделюються є не істотними. Існують явища та об'єкти, що або за своєю природою є стохастичними, або випадкові флуктуації їхніх властивостей є суттєвими і вони повинні бути враховані в моделі.

Мережі зв'язку й інфокомунікаційні системи за своєю структурою є детермінованими системами, а їхнє функціонування, наприклад, навантаження в мережі, має випадковий характер, тобто в цьому відношенні вони є стохастичними системами. Для моделювання таких систем використовуються спеціальні методи, найбільш розповсюдженим з них є статистичне моделювання.

Під статистичним моделюванням слід розуміти відтворення за допомогою комп'ютера функціонування деякого стохастичного процесу або об'єкта. Ціль такого моделювання полягає в оцінюванні середніх значень характеристик моделі. Найбільш відомими моделями, такого роду, є моделі теорії масового обслуговування. Основна задача статичного моделювання систем – це дослідження за допомогою ЕОМ їхньої еволюції в часі. Розглянемо, у загальному вигляді, основні етапи розробки таких статистичних моделей:

1. Розробка спеціальних програм, так званих генераторів або датчиків випадкових чисел. Результат роботи такої програми – випадкові числа, рівномірно розподілені у відрізку [0,1].

2. Реалізація за допомогою датчика випадкових чисел стохастичних процесів з більш складними законами розподілу ймовірностей випадкових величин.

3. Обчислення, за допомогою отриманих розподілів ймовірностей, значень величин, що характеризують модель, статистична обробку отриманих результатів.

4. Встановлення зв'язку алгоритмів моделювання з алгоритмами рішення задач обчислювальної математики за допомогою методу Монте-Карло та розробка так званих «фіктивних моделей», тобто моделей, що не мають зв'язку з об'єктом моделювання, але зручні в обчислювальному відношенні, що дозволяє обчислювати характері параметри об'єкту.

Найбільш розповсюдженим методом стохастичного моделювання є метод Монте-Карло.

Теоретичні основи методу Монте-Карло відомі вже давно. Датою народження цього методу прийнято вважати 1949 р., коли в американському журналі асоціації статистиків з'явилася стаття Метрополіса та Улама «Метод Монте-Карло». Творцями методу вважають Дж.Неймана і С.Улама. Оскільки, моделювання випадкових величин вручну – дуже трудомістка робота, то широке застосування методу почалося тільки з появою обчислювальних машин.

Сама назва «Монте-Карло» походить від назви міста в князівстві Монако, знаменитого своїми ігорними будинками. Вибір такої назви, швидше за все, пов'язаний з тим, що одним з найпростіших механічних пристроїв для одержання випадкових чисел, а, отже, і моделювання випадкових величин є рулетка. Найпростіша її схема – обертовий диск із цифрами від 0 до 9, що раптово зупиняють для визначення цифри, на яку вказує нерухома стрілка. Поєднуючи одержані в такий спосіб цифри в групи заданого розміру (наприклад, по п'ять цифр), можна одержати послідовність випадкових чисел з рівномірним законом розподілу. Такі випадкові числа складають основу розробки моделей стохастичних систем з використанням методу Монте-Карло.

Для одержання випадкових чисел з рівномірним законом розподілу використовуються спеціальні алгоритми. Числа, що одержують за допомогою цих алгоритмів, лише імітують випадкову величину з рівномірним розподілом, тому називаються псевдовипадковими.

Перший такий алгоритм був запропонований фон Нейманом у 1951 р. Він називається методом середини квадратів. Сутність цього методу полягає в наступному. Нехай задане довільне 4-значне ціле число, наприклад, 4561. Піднесемо його до квадрату, що дасть 8-значне число 20802721. Виберемо 4 середні цифри з цього числа – 8027. Знову піднесемо його до квадрату – 64432729 і виберемо 4 середні цифри: 4327. Продовжуючи зазначені рекуррентні дії, будемо мати: 7229, 2584, 7705 і т.д. У якості псевдовипадкових чисел із проміжку [0,1] можна використовувати , тобто: 0.8027; 0.4327; 0.7229 і т.д. Послідовності псевдовипадкових чисел, що одержують рекурентно з застосуванням обчислювальної техніки, мають період, величина якого залежить головним чином від розрядності представлення чисел в ЕОМ. З точки зору теорії ймовірностей – це погано. Однак у тих випадках, коли довжина послідовності псевдовипадкових чисел менше періоду цієї послідовності, можна розробляти прикладні програми для моделювання стохастичних систем за допомогою ЕОМ.

Сутність цього методу проілюструємо на простому прикладі обчислення площі криволінійної фігури (рис. 5.2).

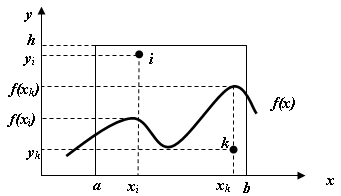
Рисунок 5.2 – До обчислення площі криволінійної фігури методом Монте-Карло

Площа, що підлягає обчисленню, обмежена зверху графіком функції , а з боків прямими і . Впишемо цю криволінійну фігуру в прямокутник висотою . Нехай деяке випадкове число – датчик випадкових чисел. Використовуючи датчик випадкових чисел, будемо випадковим чином вибирати усередині прямокутника точки з координатами в такий спосіб

.

Тут і – два різних випадкових числа. При цьому будемо вести підрахунок загальної кількості таких точок – , і кількості точок, які потрапили усередину криволінійної фігури – . Випадкова точка розташована усередині криволінійної фігури, якщо . Очевидно, що частина точок, які потрапили усередину криволінійної фігури пропорційна частині площі, що займає ця фігура в прямокутнику висотою і з основою

.

Звідси випливає, що

.

Для того щоб у такий спосіб одержати прийнятну точність обчислення площі необхідно брати близько 3000 точок. Природно, що для подібних задач слід використовувати більш ефективні чисельні методи обчислення визначених інтегралів. Що стосується методу Монте-Карло, то він більш ефективний при чисельному інтегруванні кратних інтегралів.

Що стосується розробки моделей стохастичних систем то найбільш прийнятним і широко розповсюдженим методом є метод Монте-Карло. Це пов'язано з тим, що

• визначення вихідних параметрів здійснюється з використанням досить простих алгоритмів обробки;

• забезпечується задана точність оцінок вихідних величин;

• методика організації чисельних експериментів на моделі досить проста і добре програмно реалізована.