3.2 Декомпозиція систем. Підсистеми. Елементи системи

Декомпозиція системи припускає виділення в ній двох типів компонентів: складених (підсистеми) і елементарних (елементів), що знаходяться у визначених відношеннях і утворюють у сукупності цілісну систему. Визначити поняття підсистеми можна різними способами, обмежимося тільки тими, котрі найбільш широко можуть використовуватися в різних практичних задачах. Слід зазначити, що визначаючи поняття підсистема й елемент системи, тим самим можна установити й основні методи декомпозиції систем.

Визначення. Нехай — загальна система. Підсистемою цієї системи будемо називати будь-яку підмножину , таку що . У свою чергу елементом системи будемо називати таку систему, з якої за допомогою основних операторів з'єднання можна одержати вихідну систему (можливо, використовуючи при цьому і деякі інші системи).

Необхідно відзначити, що в прикладних задачах системного аналізу термін «підсистема» використовується для визначення цілого спектра зовсім різних понять, у тому числі і для елементів системи.

Насамперед, вивчимо взаємозв'язок між поняттями елемента і системи.

Для систем , і , введемо оператори проектування:

і

такі, що

та

Наступним важливим поняттям, є поняття не взаємодіючих систем. Дві системи і вважаються не взаємодіючими (відносно ) тоді і тільки тоді, коли в цьому випадку називається незалежною декомпозицією системи .

Іншими словами, якщо в системі можна виділити такі підсистеми, що їхнє паралельне з'єднання утворить систему і, навпаки, якщо система складається з паралельно з'єднаних підсистем, то ці підсистеми є незалежними.

Існує аналогія між поняттями незалежних підсистем і лінійно – незалежною системою векторів. Відомо, що на площині будь-які два не колінеарні вектори і є лінійно незалежними, тобто лінійна комбінація таких векторів дорівнює нулеві , де і – довільні дійсні числа. При цьому будь-який вектор можна представити у вигляді лінійної комбінації виду

,

де дійсні числа і координати або проекції вектора .

Розглянемо на прикладі декомпозицію вихідної системи на незалежні підсистеми. Нехай задана система «вектор на площині». Нехай – початок вектора, а – його кінець (рис. 3.5). Тоді вектор – це система .

Систему можна представити у виді двох підсистем – проекцій на осі координат 1 і 2: і

Ці проекції є незалежними, а, отже, і підсистеми і є теж незалежними, при цьому . Розглянемо систему «трикутник на площині заданий координатами вершин» (рис. 3.6).

Нескладно переконатися, що вихідна система

може бути розділена на дві незалежні підсистеми і . Ці системи у свою чергу розпадаються на незалежні підсистеми , , і . Система вже не є незалежною. Так, зокрема її проекція на вісь 1 є «лінійною комбінацією» відповідних проекцій підсистем і :

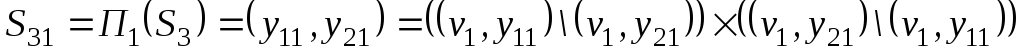
Визначення максимальної незалежної декомпозиції. Незалежна декомпозиція , де , називається максимальною тоді і тільки тоді, коли для будь-якого , не існує (нетривіальної) незалежної декомпозиції.

Повернемося до приклада «вектор на площині». Його проекції на координатні осі утворять максимальну незалежну декомпозицію цієї системи.

Необхідно встановити, чи володіє система максимальною незалежною декомпозицією чи ні. Очевидно, що, якщо об'єкти системи утворені кінцевим числом компонент, тобто і для деяких і , то для неї існує максимальна незалежна декомпозиція.

Розглянемо основні методи декомпозиції систем на елементи:

• Будь-яка система допускає декомпозицію в з'єднані каскадно й охоплені зворотним зв'язком елементи, де і , а і допоміжні множини (рис. 3.7).

• Будь-яка система допускає декомпозицію в з'єднані каскадно елементи (рис. 3.8).