Составим уравнение равновесия пирамиды, спроектировав все силы, действующие по его граням, на ось õ. Проекция объемной силы в уравнение не входит, так как представляет собой величи- ну высшего порядка малости по сравнению с проекциями поверхностных сил:

Составив уравнения проекции сил на оси y и z, получим два аналогичных уравнения. В результате будем иметь три уравнения равновесия:

(14.1.6-1)

Эти уравнения связывают нагрузку на поверхности тела с напряжениями теле, т.е. представляют граничные условия задачи теории упругости. Система уравнений теории упругости (14.1.2-2), (14.1.9) и (14.1.16), дополненная граничными условиями по напряжениям (14.1.6-1) и по перемещениям представляет общую постановку собой краевой задачи теории упругости.

Методы решения краевой задачи теории упругости, как точные, так и приближенные можно разделить на две группы: решение в перемещениях и напряжениях.

В первом случае за основные неизвестные принимают перемещения точек упругого тела:

u= f1(x,y,z),

v= f2(x,y,z),

w= f3(x,y,z).

Для получения решений нужно в уравнения обобщенного закона Гука (14.1.16) подставить геометрические соотношения (14.1.9), т.е. выразить напряжения через перемещения, и затем полученные выражения подставить в уравнения равновесия (14.1.2-2), в результате чего получаются три уравнения

ψ1(u,v,w) = 0, ψ2(u,v,w) = 0, ψ3(u,v,w) = 0,

решение которых даст искомые перемещения. Отметим, что граничные условия в напряжениях так-

же необходимо преобразовать в перемещения подобным образом.

Во втором случае за неизвестные принимают компоненты напряжения:

σx = Ô1(x, y, z), σy = Ô2(x, y, z), σz = Ô3(x, y, z),

τxy = Ô4(x, y, z), τyz = Ô5(x, y, z), τzx = Ô6(x, y, z).

Ñпомощью обобщенного закона Гука (14.1.5-

3)и уравнений равновесия (14.1.2-2), шесть уравнений неразрывности деформаций (14.1.4-1) можно записать через напряжения:

F1(σ x,…,τzx) = 0 … F6(σx,…, τzx) = 0.

Решение этих уравнений вместе с граничными условиями дает искомые компоненты тензора напряжений.

14.1.7 - Плоская задача теории упругости

Существуют два важных в практическом отношении частных случая напряженно-деформиро- ванного состояния тела, когда решение задачи теории упругости существенно упрощается. Это плоское деформированное и плоское напряженное состояния.

При плоском деформированном состоянии (см. Рис. 14.1.7_1 а) точки тела не могут перемещаться вдоль оси z из-за препятствия со стороны соседних элементов, т.е. вдали от торцов при большой длине тела перемещения w вдоль оси z отсутствуют (w = 0). Нагрузка, действующая на тело, постоянна вдоль оси z, но может меняться в плоскости õÎó. В таком случае любой элемент единич- ной толщины, вырезанный двумя параллельными сечениями, перпендикулярными оси z, на достаточно большом расстоянии от торцов находится в одинаковых условиях с соседними и испытывает плоское деформированное состояние, перемещения u è v не зависят от координаты z.

При плоском напряженном состоянии размеры тела вдоль оси z малы (см. Рис. 14.1.7_1, б), а боковые плоскости, параллельные õÎó свободны от нагрузки, т.е. напряжения σz, τzx è τzy на этих плоскостях равны нулю. Ввиду малой толщины можно предположить, что и внутри тела, по плоскостям, параллельным õÎó, напряжения пренебрежимо малы, а напряжения σx, σy è τxy не зависят от коор-

динаты z. Перемещения w вдоль оси z происходят, но они представляют собой функцию напряжений

σx è σy.

Основные уравнения теории упругости в слу- чае плоского деформированного состояния упростятся следующим образом. Все искомые функции станут функциями двух координат. Кроме того равны нулю перемещение w, компоненты тензора деформации, εz, γzx è γzy, компоненты тензора напря-

жений τyz, τzx.

Из третьего уравнения закона Гука (14.1.5-1), считая деформацию εz = 0, получаем:

Подставив в уравнения (14.1.5-3) выражение (14.1.7-1) и заменив модуль упругости, модуль сдвига и коэффициент Пуассона приведенными величинами:

получим уравнения закона Гука в виде:

(14.1.7-2)

Для плоского напряженного состояния равны нулю деформации γyz è γzx, напряжения σz, τyz è τzx. Уравнения закона Гука принимают вид:

Из трех уравнений равновесия (14.1.2-2) ввиду того, что все напряжения не зависят от z, a τyz è τzx равны нулю, остается два:

(14.1.7-4)

Условия на поверхности (14.1.22) примут вид:

(14.1.7-5)

Из шести уравнений совместности (14.1.4-1) вследствие того, что εx,εy è γxy не зависят от z, εz равно нулю или тоже не зависит от z, à γyz è γzx равны нулю, останется одно:

(14.1.7-6)

Если здесь заменить деформации напряжениями, пользуясь уравнениями (14.1.7-3), и выполнить преобразования уравнение совместности деформации может быть представлено в напряжениях:

èëè

(14.1.7-7)

(14.1.7-3)

Рисунок 14.1.7_1 - Плоское деформированное (а) и плоское напряженное (б) состояния

ãäå 2 - оператор Лапласа.

Из совместного решения этого уравнения и уравнений равновесия (14.1.7-4) могут быть найдены все три неизвестные компоненты напряжения в случае плоской задачи. Так как в эти уравнения не входят упругие постоянные, можно заключить, что в такой постановке задачи напряженное состояние не зависит от материала.

В случае, если объемные силы отсутствуют, задача может быть сведена к отысканию единственной функции, так называемой функции напряжений ϕ. В теории упругости доказано, что существует функция ϕ, через которую могут быть выражены все три неизвестные компоненты напряжения σõ, σy è τõó следующим образом:

(14.1.7-8).

Можно убедиться, что эти выражения удовлетворяют уравнениям равновесия (14.1.7-4). Подставив в уравнение (14.1.7-70), получим бигармоническое уравнение:

(14.1.7-9)

Решение плоской задачи сводится к отысканию функции ϕ, удовлетворяющей этому уравнению и условиям на поверхности. Существует аналитическое решение этой задачи для некоторых простейших вариантов формы тела. При применении численных методов решение плоской задачи существенно менее трудоемко, чем пространственной.

14.1.8 - Пластическая деформация материала. Простое и сложное нагружение

Для описания явления пластической деформации воспользуемся типичной зависимостью деформации от напряжения (см. Рис. 14.1.8_1), получаемой экспериментально при растяжении образцов из большинства конструкционных материалов.

Если напряжение σ не превышает предела упругости σe, то зависимость между напряжением σ и деформацией ε оказывается линейной:

σ = Εε.

В этой зависимости модуль упругости материала E равен тангенсу угла наклона линейного участка диаграммы (σ - ε). Линейная зависимость между напряжениями и деформациями характерна для упругости, но критерий упругого поведения материалов состоит в том, что после снятия внешнего воздействия все размеры детали восстанавливаются. На диаграмме (σ-ε) (см. Рис. 14.1.8_1) это проявляется следующим образом. Если в точке А0 ïðè σ < σ e прекратить нагружение материала и снять

внешнюю нагрузку, деформация материала исчезнет (точка, изображающая на диаграмме состояние материала, вернется в начало координат). При возрастании напряжений выше предела упругости σ > σ e зависимость σ îò ε перестает быть линейной. Если в некоторый момент нагружения, соответствующий точке А, прекратить нагружение и снять нагрузку, то разгрузка пойдет по прямой АА1, приблизительно параллельной начальному участку. Точка А перейдет в точку А1, и в материале сохранится остаточная деформация εÐ, которая представляет собой пластическую деформацию в материале, образовавшуюся при его нагружении. Полная деформация складывается из упругой εe и пласти- ческой ε p:

Уравнение (14.1.8-1) справедливо для любого момента деформации. Пластическая деформация существует одновременно с упругой, поэтому следует говорить об упругопластических деформациях материала. Упругая деформация для металлов составляет 0,2…0,8%, пластическая может доходить до 20…40%.

При повторном нагружении из точки А1 процесс нагружения пойдет по прямой А1À, ò.å. ïðå-

Рисунок 14.1.8_1 - Диаграмма деформирования материала

дел упругости возрастет. Таким образом, после предварительной пластической деформации происходит упрочнение материала, при дальнейшем нагружении (переход от точки А к точке В) деформирование идет так же, как в случае однократного нагружения.

Диаграммы (σ-ε), получаемые при сжатии пластичных материалов, мало отличаются от диаграмм растяжения. Предел упругости в точке A1 (см. Рис. 14.1.8_2) по абсолютной величине такой же, как при растяжении. Иное поведение материала наблюдается, если сжатию предшествовало растяжение в пластической области. Предел упругости существенно уменьшается (точка A*). Этот эффект называется эффектом Баушингера и объясняется остаточным взаимодействием между зернами материала после деформации растяжения.

Влияние температуры на диаграмму растяжения выражается в снижении модуля упругости и п- редела текучести с ростом температуры практически для всех металлов (см. Рис. 14.1.8_3).

Наиболее важными характеристиками сопротивления материала внешним нагрузкам являются пределы текучести и прочности. Предел текучес-

ти характеризует сопротивление материала возникновению пластических деформаций. Так как переход от участка упругости к зоне появления пластических деформаций для большинства материалов носит плавный характер, то условились пределом текучести считать напряжение σ02, соответствующее значению остаточной деформации 0,2%. В отличие от него предел прочности σb– напряжение, соответствующее разрушению образца. Обычно предел текучести составляет (0,5…0,9)σb.

Нагружение считают простым, если все компоненты нагрузок возрастают от нуля одновременно так, что соотношения между ними в любой момент времени сохраняются неизменными, т.е. все внешние силы возрастают пропорционально одному общему параметру. Сами нагрузки при этом могут быть сколь угодно сложны: сосредоточенные силы, равномерно или неравномерно распределенные как по наружной поверхности тела и т.д. Если неизменное соотношение между внешними силами не соблюдается (например, часть сил действует ранее других, или, начав вместе, некоторые из сил прекращают свое действие, а остальные продолжают нарастать и т.д.), то такое нагружение на-

зывают сложным, хотя нагрузка по количеству сил, их расположению может быть и простой. Простое и сложное нагружение не следует путать с простым (одноосным) и сложным (когда два или три главных напряжения для рассматриваемой точки отлич- ны от нуля) напряженным состоянием.

Деформацию в некоторой точке называют активной, если интенсивность напряжения для этой точки в каждый момент нагружения имеет значе- ние, превышающее все предшествующие его зна- чения. В случае простого нагружения это происходит при монотонном возрастании нагрузки. Если при деформации интенсивность напряжения меньше предшествующего его значения, деформацию называют пассивной.

14.1.9 - Модели упруго-пластичес- ких деформаций. Метод переменных параметров упругости

Âтеории пластичности используют две группы математических моделей поведения материалов. Их называют теорией упруго-пластических деформаций и теорией течения.

Âпервой группе устанавливают связь между напряжениями и деформациями. Во второй – между напряжениями и бесконечно малыми приращениями деформаций при бесконечно малых приращениях напряжений.

Достоинство моделей первой группы – простота, однако модели этой группы не описывают сложного нагружения и не позволяют учитывать историю нагружения при определении пластических деформаций. Модели второй группы свободны от этих ограничений, но более сложны в использовании. Они не будут рассматриваться здесь,

ñними можно познакомиться в литературе по теории пластичности, например в [14.8.25].

Âоснове теории упруго-пластических деформаций лежит экспериментально обоснованное представление о наличии однозначной зависимости между суммарными деформациями и напряжениями в теле. Для изотропного тела эти зависимости имеют вид:

(14.1.9-1)

ãäå ε0 = (εx+εy+εz )/3 - средние деформации;

σ0 = (σx+σy+σz )/3 - средние напряжения. Экспериментально установлено, что пласти-

ческая деформация не приводит к изменению объема материала, которое пропорционально среднему напряжению. С учетом теплового расширения при изменении температуры:

(14.1.9-2)

В уравнениях (14.1.9-1) величина ψ называется параметром пластичности и вводится как:

(14.1.9-3)

ãäå εi è σi - интенсивности деформаций и напряжений рассмотренные выше.

В теории пластичности часто используется гипотеза единой кривой, состоящая в том, что зависимость между интенсивностями деформаций и напряжений εi = f(σi ), получаемая экспериментально при одноосном растяжении, остается неизменной для любого напряженного состояния. Таким образом, параметр пластичности, вообще говоря, не константа, а функция интенсивности напряжений.

Для того, чтобы понять физический смысл параметра пластичности рассмотрим одноосное растяжение стержня. Все компоненты напряжения, кроме одной равны нулю.

Пусть σx = σ, тогда для интенсивности напряжений из (14.1.1-2) получаем σi = σ. Если продольная деформация стержня εx = ε, то деформации в -

поперечных направлениях εy = -µ*ε è εz = -µ*ε . Здесь µ* - коэффициент Пуассона для пластичес-

ких деформаций, в случае упругих деформаций он равен µ..

Для интенсивности деформаций из (14.1.3-4) находим:

.

Тогда для одноосного растяжения стержня получаем:

(14.1.9-4)

Здесь σ* = Eε - условное напряжение, которое соответствует деформации e в случае, если бы тело было упругим (точка A* íà Ðèñ. 14.1.8_2).

Таким образом, параметр пластичности можно интерпретировать как отношение напряжений в упругом теле к напряжениям в пластическом теле при одних и тех же деформациях.

На упругом участке кривой деформирования ψ = 1. В этом случае уравнения (14.1.9-1) можно привести к обобщенному закону Гука (14.1.5-3). Так, для рассмотренного выше случая одноосного растяжения стержня средняя деформация равна ε0 = ε(1-2µ)/3, среднее напряжение σ0 = σ/3 è èç (14.1.9-1) ïðè ψ = 1 получаем σ = Eε.

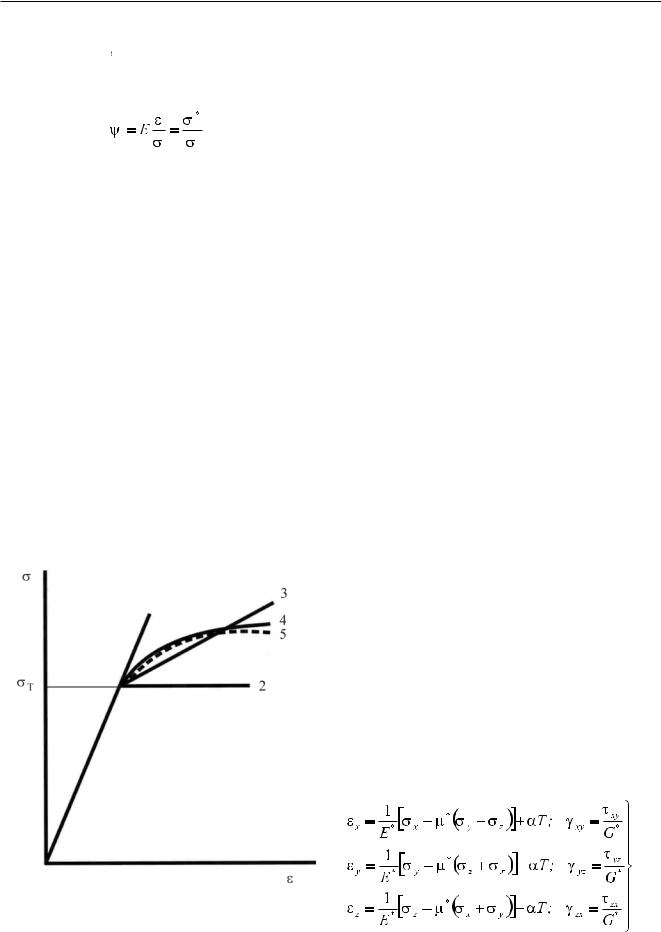
Для математического описания кривой деформирования σi = f(εi) используют различные соотношения (модели) (см. Рис. 14.1.9_1). Простейшая из них – модель идеального упруго-пластического тела (кривая 2), в которой пренебрегают упрочнением материала при пластической деформации. По

Рисунок 14.1.9_1 - Схематизация диаграммы деформирования

мере нагружения при напряжениях менее предела текучести σÒ деформация упругая, она увеличивается пропорционально напряжению (кривая 1). При дальнейшем нагружении деформация увеличивается без увеличения напряжений. Благодаря своей простоте модель используется для оценки эффектов пластической деформации в аналитических расчетах. При развитых пластических деформациях материалов с площадкой текучести (низкоуглеродистых нелегированных сталей, например) эта модель позволяет получать количественные результаты с достаточной для практики точностью. Далее в порядке увеличения точности следуют модели линейного (кривая 3) и степенного (кривая 4) упрочнения. Последние наиболее близки к реальной кривой упрочнения материала (кривая 5). При использовании современных численных методов обычно используются модели того уровня точности, который обеспечивается экспериментальными данными, а не сложностью расчетов.

Система уравнений, описывающая упруго-пла- стическое напряженно-деформированное состояние тела, отличается от системы уравнений теории упругости только соотношениями между деформациями и напряжениями. Она включает в себя уравнения равновесия (14.1.2-2), условия совместности деформаций (14.1.4-1), физические уравнения для упруго-пластического тела (14.1.9-1), а также соотношение (14.1.9-4) для параметра пластичности ψ. Решение должно, кроме того, удовлетворять граничным условиям в перемещениях и напряжениях.

Рассмотрим предложенный И.А.Биргером метод расчета упруго-пластического напряженного состояния – метод переменных параметров упругости. Он сводит упруго-пластическую задачу к цепочке упругих задач в результате применения процесса последовательных приближений. В основе метода лежит использование обобщенного закона Гука, в котором модуль упругости и коэффициент Пуассона зависят от напряжений и поэтому имеют разные значения в разных точках тела.

Уравнения обобщенного закона Гука записываются в виде:

(14.1.9-5)

Параметры E*, G* è µ* зависят от отношения интенсивностей напряжений и деформаций. В ча- стном случае, когда пренебрегают сжимаемостью материала:

(14.1.9-6)

Процесс последовательных приближений реализуется следующим образом. В первом приближении принимается, что переменные параметры упругости равны параметрам упругости, и решается упругая задача, в результате чего определяются компоненты напряжения и деформации перво-

го приближения σx1, …., τxy1, …, εx1,…, γxy1,… По этим величинам в каждой точке тела вычисляются

интенсивности напряжений и деформаций в первом приближении σi1 è εi1. В координатах σi - εi. (см. Рис. 14.1.9_2) напряженное и деформированное состояние некоторой точки тела изображается точ- кой 1, лежащей на луче, тангенс угла наклона которого пропорционален величине E = 3G.

Во втором приближении вносится поправка для величины E*. В соответствии с (14.1.9-6) она принимается равной отношению интенсивности напряжений σ i1 к интенсивности деформаций εi1 по диаграмме σi-εi (см. Рис. 14.1.9_2). Параметры E* è G* будут различными в разных точках тела. Таким образом, возникает задача определения напряжений в условно неоднородном теле, параметры упругости в различных точках которого раз-

Рисунок 14.1.9_2 - Метод переменных параметров упругости

личны. Далее решают эту задачу, определяют компоненты напряжения и деформации σx2, …, τxy2, …, εx2,…, γxy2,…являющиеся вторым приближением. По этим величинам в каждой точке тела вычисляются интенсивности напряжений и деформаций во втором приближении σi2 è εi2 (точка 2 на Рис. 14.1.9_2).

В третьем приближении величина E* вычисляется как отношение интенсивности напряжений σ*i2 к интенсивности деформаций εi2 по диаграмме деформирования. Далее вычисляют компоненты напряжения и деформации третьего приближения и т.д. Расчет продолжается до тех пор, пока разница результатов в очередном и предыдущем приближениях не станет достаточно малой. Практика расчетов показывает, что процесс хорошо сходится уже на втором – третьем приближениях.

Подобная процедура используется, например, при расчете на прочность дисков ГТД.

14.1.10 - Поведение конструкций при разгрузке. Остаточные напря-

жения

Эффекты, связанные с пластическим деформированием, рассмотрим на примере чистого изгиба стержня прямоугольного сечения. Для простоты используем модель идеального упруго-пластичес- кого тела без упрочнения (см. Рис. 14.1.9_1). Будем считать, что на стержень действуют сосредото- ченные изгибающие моменты M (см. Рис. 14.1.10_1), которые увеличиваются постепенно.

Максимальные напряжения возникают, как известно, в крайних верхних и нижних волокнах. На стадии упругого деформирования они равны:

(14.1.10-1)

ãäå W – момент сопротивления сечения.

Эти напряжения достигают предела текучести при изгибающем моменте:

Пусть изгибающий момент превосходит это значение. При этом в стержне возникает область пластических деформаций, упругими остаются волокна на расстоянии менее h1/2 от нейтральной линии (см. Рис. 14.1.10_1б). В области пластичес-

ких деформаций в соответствии с принятой моделью идеального упруго-пластического тела напряжения равны пределу текучести, в упругой области - пропорциональны расстоянию от нейтральной линии:

(14.1.10-2)

Из условия равновесия

(14.1.10-3)

находим размер пластической зоны:

(14.1.10-4)

Отсюда видно, что с увеличением изгибающего момента пластическая зона постепенно увеличивается, и при некотором предельном значе- нии изгибающего момента MÏÐÅÄ все сечение стержня переходит в пластическое состояние (см. Рис. 14.1.10_1д). Дальнейшее увеличение изгибающего момента в рамках принятой модели идеального упруго-пластического материала невозможно, следовательно он дает оценку предельной несущей способности стержня. Его значение вытекает из

(14.1.10-4) ïðè h1 = 0: MÏÐÅÄ = σTbh2/4.

При разгрузке, как показывают эксперименты, уменьшение напряжений пропорционально уменьшению деформаций. В случае сложного напряженного состояния эта же зависимость формулируется в отношении интенсивностей напряжений и деформаций:

Напряжения и деформации разгрузки могут быть определены из решения задачи теории упругости для внешних сил, равных разностям сил при нагружении и остающихся после разгрузки. В слу- чае полной разгрузки решается задача теории упругости для внешних сил, нагружающих тело. Это справедливо в том случае, если при разгрузке материал не выходит вновь за пределы упругости.

Поле остаточных напряжений удовлетворяет уравнениям равновесия и граничным условиям по напряжениям, соответствующим нагрузкам, оставшимся после разгрузки. В случае полной разгрузки поле остаточных напряжений должно быть самоуравновешенным. Остаточные напряжения и деформации определяются как разность напряжений и деформаций, достигнутых на стадии нагрузки, и напряжений и деформаций разгрузки:

Вернемся к ситуации, когда в стержне под действием изгибающего момента M возникла пласти- ческая зона размером h – h1 и рассмотрим процесс разгрузки. Напряжение разгрузки, получающееся из решения упругой задачи для изгибающего мо-