
Теоретические основы электротехники-1
.pdf
Глава 8. Расчет электрических цепей при несинусоидальных токах 343
и, соответственно, к появлению перенапряжений на отдельных участках цепи, к нежелательному влиянию гармоник звуковой частоты на радио- и телефонную связь, к возникновению в трехфазных двигателях магнитных полей, вращающихся против направления вращения ротора (например, при k 5, 11, . . .) и, следовательно, вызывающих торможение ротора и добавочные потери в двигателях.
Однако отсюда не следует, что во всех без исключения устройствах всегда необходимо стремиться к получению синусоидальных токов и напряжений. Это, безусловно, относится к мощным электроэнергетическим устройствам. Однако в маломощных устройствах автоматического управления и регулирования, а также в ряде специальных радиотехнических, электроизмерительных и различных электронных устройств оказывается необходимым как раз получить формы кривых напряжения и тока, отличающиеся от синусоидальных, т. е. содержащие высшие гармоники. Некоторые из таких устройств будут рассмотрены в главах о нелинейных электрических цепях.
8.5. Особенности поведения высших гармоник в трехфазных цепях
Предположим, что фазные ЭДС симметрично устроенного трехфазного генератора содержат высшие гармоники. Кривые ЭДС во всех фазах по форме одинаковы и сдвинуты в каждой последующей фазе относительно предыдущей на угол 2 /3, где 2 — период всей кривой ЭДС, равный периоду первой гармоники. Так как период k-й гармоники в k раз меньше периода первой гармоники, то угол сдвига k-й гармоники в последующей фазе по отношению к предыдущей фазе равен k2 /3. Таким образом, все гармоники, порядок которых кратен числу фаз, т. е. кратен трем (k 3, 6, 9, 12, 15, . . .), сдвинуты друг относительно друга на угол, равный 2 , умноженный на целое число, т. е. эти гармоники находятся в фазе друг с другом и образуют симметричные системы нулевой последовательности.
Гармоники, для которых k – 1 делится на три (k 4, 7, 10, 13, . . .), образуют, как нетрудно убедиться, симметричные системы прямой последовательности.
Гармоники, для которых k + 1 делится на три (k 2, 5, 8, 11, . . .), образуют симметричные системы обратной последовательности.
Из этих свойств вытекает ряд особенностей поведения высших гармоник в трехфазных цепях.
Предположим, что обмотки генератора соединены треугольником. Сумма первых гармоник фазных ЭДС в контуре треугольника равна нулю. Это имеет место также для всех высших гармоник, порядок которых не кратен трем. Гармоники же, порядок которых кратен трем, совпадают по фазе во всех фазных обмотках, и их сумма не равна нулю. Эта суммарная ЭДС вызывает в контуре треугольника ток даже при отсутствии нагрузки генератора. Падения напряжения в обмотках вследствие протекания этого тока компенсируют вызывающие ток ЭДС. Поэтому напряжения на зажимах обмотки не содержат гармоник, порядок которых кратен трем.
То же самое имеет место при соединении обмоток трансформатора треугольником, если фазные ЭДС в обмотках трансформатора симметричны. Обычно,


Глава 8. Расчет электрических цепей при несинусоидальных токах 345
Важным случаем является симметрия кривых относительно оси абсцисс (рис. 8.6), при которой выполняется условие
f (t) f (t T 2),
2),
т. е. отрицательная полуволна является зеркальным изображением сдвинутой на половину периода положительной полуволны.
Ðèñ. 8.6 |
Ðèñ. 8.7 |
Если кривая симметрична относительно оси абсцисс, ряд Фурье не содержит постоянной составляющей и четных гармоник, так как для них не удовлетворяется приведенное ранее условие симметрии. Действительно, сдвигу функции, а следовательно, и первой гармоники на T/2 соответствует сдвиг четных гармоник на целое число полных периодов, и значения этих гармоник не меняют своего знака. Таким образом, любая симметричная относительно оси абсцисс кривая содержит только нечетные гармоники.
Это положение имеет исключительно большое значение. Основываясь на нем, можно утверждать, что при симметричном устройстве вращающихся генераторов ЭДС в их обмотках не содержат четных гармоник, а также если условия прохождения тока по цепи одинаковы в обоих направлениях, то при симметричной ЭДС и ток не будет содержать четных гармоник. В линейных электрических цепях с постоянными параметрами условия прохождения тока в обоих направлениях всегда одинаковы. Эти условия могут быть неодинаковы в цепях с изменяющимися параметрами, например в нелинейных цепях с выпрямителями. В последнем случае появляются постоянная составляющая и четные гармоники в кривой тока.
Примером симметричной относительно оси абсцисс кривой является кривая трапецеидальной формы, приведенная на рис. 8.7. Разложение ее в ряд Фурье имеет вид
|
2A T |
1 |
|
1 |
|
|
|
||||
f (t) |
|
|
|
sin0, sin0t |
|
sin 30, sin 30t |
|
|
sin50, sin50t |
|
, |
|
|
|
|
|
|
||||||
|
2 |
|
, |
32 |
|
5 |
2 |
|
|
|
|
что легко получается, если воспользоваться приведенными ранее формулами для Bk è Ck. Ïðè , T/4 получаем равнобедренный треугольник, и разложение принимает вид
|
8A |
1 |
|
1 |
|
|
|
||
f (t) |
|
sin0t |
|
sin 30t |
|
|
sin50t |
|
. |
2 |
32 |
|
2 |
|
|||||
|
|
|
5 |
|
|
|
|||
Ïðè , 0 получаем прямоугольную кривую, для которой

346 Часть 2. Теория линейных электрических цепей
|
4A |
1 |
|
1 |
|
|
|
|
f (t) |
|
sin0t |
|
sin 30t |
|
sin50t |
|
. |
2 |
3 |
5 |
|
|||||
|
|
|
|
|
|
|||
Из этих разложений видно, что в них отсутствуют постоянные составляющие и четные гармоники.
Ðèñ. 8.8 Ðèñ. 8.9
Может быть симметрия кривых другого характера. На рис. 8.8 изображена кривая, симметричная относительно оси ординат. Изображаемая ею функция удовлетворяет условию f(t) f(–t). Нетрудно убедиться, что при этом
B1 B2 B3 Bk 0 и разложение в ряд Фурье имеет вид
f (t) A0 C1 cos0t C2 cos20t C3 cos 30t Ck cos k0t
Если кривая симметрична относительно начала координат (рис. 8.9), то f(t) –f(–t). В этом случае
A0 C1 C2 C3 Ck 0 и ряд Фурье имеет вид
f (t) B1 sin0t B2 sin20t B3 sin 30t Bk sin k0t
Подчеркнем, что условие симметрии относительно оси абсцисс не зависит от выбора начала отсчета времени, т. е. является свойством самих кривых, тогда как рассмотренные остальные виды симметрии связаны с выбором начала отсчета времени.
8.7. Представление ряда Фурье в комплексной форме
В ряде случаев целесообразно представить ряд Фурье в комплексной форме. Это особенно полезно будет при рассмотрении в гл. 11 частотного метода анализа процессов в электрических цепях. Ранее ряд Фурье был представлен в виде
k
f (t) A0 (Bk sin k0t Ck cos k0t).
k1
Âвыражениях для A0, Bk è Ck нам будет удобнее взять пределы интегрирования не от 0 до T, à îò —T/2 äî +T/2. Будем иметь
|
|
1 |
T 2 |
|
|
2 |
T 2 |
|
|
2 |
T 2 |
|
A0 |
|
f (t)dt; |
Bk |
|
f (t)sin k0t dt; |
Ck |
|
f (t)cos k0t dt, |
||||
T |
T |
T |
||||||||||
|
|
T 2 |
|
|
T 2 |
|
|
T 2 |
причем 0 2 /T — угловая частота первой гармоники.


348 Часть 2. Теория линейных электрических цепей
# |
2 |
F( jk0 e |
jk0t & |
|
2 |
F(k0 cos(k0t k ) |
2 |
F(k0 sin(k0t Α k ), |
Re % |
|
( |
|
|
||||
|
T |
T |
||||||
T |
|
|
|
|
|
|||
ãäå Αk /2 + k.
Таким образом, величина
T2 F(k0 ejΑk j T2 F(k0 ej k j T2 F( jk0
представляет собой комплексную амплитуду k-й гармоники
|
|
|
|
|
jΑk |
, |
|
Ak Ak e |
|
||||||
ãäå |
|
|
|
|
|
|
|
A |
|
|
2 |
F(k0 . |
|||
k |
T |
||||||
|
|
|
|
|
|||
|
|
|
|
|
|
||
Совокупность комплексных амплитуд всех гармоник данной функции может
рассматриваться как дискретный спектр этой функции. Его можно представить |
||
|
на графике в виде спектра значений амплитуд и |
|
|
спектра значений фаз. По оси абсцисс откладыва- |
|
|
ем частоту, которая имеет дискретные значения, |
|
|
равные частотам гармоник. Для каждой частоты |
|
|
гармоник откладываем от оси абсцисс параллельно |
|
|
оси ординат отрезки, длины которых равны ампли- |
|
|
тудам Ak или начальным фазам Αk гармоник. При |
|
|
ýòîì Ak > 0, à Αk может быть как положительным, |
|
|
так и отрицательным. Такие характеристики носят |
|
Ðèñ. 8.10 |
название д и с к р е т н ы х с п е к т р о в или д и с - |
|
ê ð å ò í û õ ÷ à ñ ò î ò í û õ õ à ð à ê ò å ð è ñ ò è ê — |
||
|
||
соответственно, а м п л и т у д н о - ч а с т о т н о й и ф а з о - ч а с т о т н о й х а - р а к т е р и с т и к.
На рис. 8.10 изображена дискретная амплитудно-частотная характеристика для функции времени, показанной на рис. 8.7, при , 0.
8.8. Биения колебаний
На практике используются несинусоидальные токи и напряжения, которые не могут быть представлены в виде ряда Фурье, содержащего составляющие с частотами, кратными основной частоте, и вместе с тем обладают в известном отношении периодичностью своих изменений. Сюда относятся несинусоидальные токи и напряжения, изображаемые кривыми с периодической огибающей. К ним принадлежат так называемые б и е н и я к о л е б а н и й и м о д у л я ц и я к о л е - б а н и й.
Рассмотрим случай биения колебаний. Пусть в некоторой цепи налагаются два синусоидальных тока: i1 Im sin 01t è i2 Im sin 02t, имеющие одинаковые амплитуды, но разные частоты, причем частоты 01 è 02 близки друг к другу, так что разность их значительно меньше каждой из них:
 01 02
01 02  Ν 01 è
Ν 01 è  01 02
01 02  Ν 02 .
Ν 02 .

Глава 8. Расчет электрических цепей при несинусоидальных токах 349
Результирующий действительный ток в цепи при этом равен
|
|
i i |
i |
|
|
I |
|
|
(sin0 t sin0 |
|
t) 2I |
|
cos |
01 02 |
t sin |
01 02 |
t. |
|||||||||||||
|
|
2 |
m |
2 |
m |
|
|
|||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Òàê êàê |
|
01 02 |
|
|
Ν |
01 02 |
|
, то кривую тока i можно рассматривать как синусоиду |
||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
2 |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
с угловой частотой |
1 |
|
|
|
|
|
, амплитуда которой изменяется сравнительно мед- |
|||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ленно по закону 2Im |
|
cos |
|
1 |
|
|
t |
. |
|
|
|
|
|
|
|
|||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Так как амплитуда есть величина существенно положительная, а величина
cos 01 02 t меняет знак в моменты перехода ее через нуль, то это равносильно
2 скачкообразному изменению в эти моменты времени фазы синусоидальных ко-
лебаний с частотой |
01 |
02 |
íà óãîë . |
2 |
|
||
|
|
|
На рис. 8.11 изображены биения колебаний для случая |
01 02 |
26/3, ò. å. |
|||||
0 0 |
2 |
||||||
|
|
|
|
|
|||
|
|
|
|
1 |
|
||
для случая 01/02 29/23 èëè 02/01 23/29. |
|
|
|
|
|||
Частотой биений fá принято называть |
|
|
|
|
|||
частоту, определяемую числом максимумов |
|
|
|
|
|||
огибающей кривой в единицу времени. Со- |
|
|
|
|
|||
ответственно, величину Tá 1/fá (ðèñ. 8.11) |
|
|
|
|
|||
называют периодом биений. Таким обра- |
|
|
|
|
|||
зом, период биений равен половине перио- |
|
|
|
|
|||
да функции cos |
01 02 |
t. |
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
||
Легко усмотреть из рисунка, что харак- |
|
|
|
|
|||
тер результирующей кривой не повторяется |
|
|
|
|
|||
в двух соседних периодах биений. В рас- |
Ðèñ. 8.11 |
|
|||||
смотренном примере характер результи- |
|
||||||
|
|
|
|
||||
рующей кривой будет повторяться только через три периода функции
cos 01 02 t, т. е. через 6Tá, так как в этом интервале времени укладывается целое 2
число периодов функции sin 01 02 t, и число скачкообразных изменений ее 2
фазы на угол является четным числом 6.
Таким образом, период результирующей кривой больше периода биений. Если отношение 0 /02 является иррациональным числом, то период результирующей кривой обращается в бесконечность и, следовательно, эта кривая не является периодической. Тем не менее, понятие о периоде биений Tá сохраняет определенный смысл.

350 Часть 2. Теория линейных электрических цепей
Явление биений колебаний с успехом используется для установления отклонения частоты 01 колебаний в одной системе от частоты 02 колебаний в другой системе. Измеряя частоту биений, получаем возможность наблюдать весьма малые отклонения 0 0 – 02 по сравнению с самими величинами 0 è 02.
Так как результирующая кривая i f(t) в общем случае не является периоди- ческой, то для вычисления действующего тока i f(t), строго говоря, мы не можем пользоваться методами, установленными в § 8.3.
Однако если условиться под действующим значением I понимать среднее квадратическое значение тока i f(t) за достаточно большой промежуток времени , >> Tá, то с большой точностью можно вычислить значение I как корень квадратный из суммы квадратов действующих значений составляющих, имеющих частоты 0 è 02. Так, в рассмотренном примере при одинаковых амплитудах Im этих составляющих имеем
|
|
1 , |
|
|
I |
m |
2 |
I |
m |
2 |
|
|
|
2I |
m |
|
|||
I |
|
|
i2 (t)dt |
|
|
|
|
|
|
I |
|
|
|
, |
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
, |
|
|
|
2 |
|
2 |
|
m |
|
2 |
|
||||||
|
|
0 |
|
|
|
|
|
|
|
|
|||||||||
т. е. в этом случае значение действующего тока, которое покажет обычный прибор переменного тока, равно половине максимума огибающей кривой.
8.9. Модулированные колебания
Другим видом несинусоидальных токов, изображаемых кривой с периодической огибающей, являются модулированные токи. В случае так называемой а м п л и - т у д н о й м о д у л я ц и и они описываются уравнением
i I m sin0t I 0 (1 msin Τt)sin0t,
причем Τ — ч а с т о т а м о д у л я ц и и — много меньше частоты 0, называемой н е с у щ е й ч а с т о т о й. Коэффициент m, лежащий в пределах 0 < m < 1, называют к о э ф ф и ц и е н т о м м о д у л я ц и и. Таким образом, модулированный ток можно рассматривать как ток частоты 0, амплитуда которого изменяется пе-
риодически с частотой Τ (ðèñ. 8.12). |
|
|
|
|
|||||||
|
|
|
|
Модуляция применяется в проводной и радио- |
|||||||
|
|
|
связи. В передающем устройстве на колебания с |
||||||||
|
|
|
основной несущей частотой 0 воздействуют со |
||||||||
|
|
|
звуковой частотой Τ, создавая таким образом мо- |
||||||||
|
|
|
дулированные колебания. Модуляция осуществ- |
||||||||
|
|
|
ляется обычно с помощью нелинейных элементов |
||||||||
|
|
|
электрической цепи, например путем подачи коле- |
||||||||
|
|
|
баний несущей и звуковой частот на сетку элек- |
||||||||
Ðèñ. 8.12 |
|
|
тронной лампы и подбора условий работы лампы |
||||||||
|
|
на нелинейном участке ее характеристики. |
|||||||||
Переписав выражение для модулированного тока в форме |
|||||||||||
i I |
|
sin0t |
1 |
mI |
|
cos(0 Τt |
1 |
mI |
|
cos(0 Τt, |
|
0 |
2 |
0 |
2 |
0 |
|||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||

Вопросы, задачи и упражнения к главам 6, 7 и 8
6.1. Резонанс при последовательном соединении элементов r, L, C
ВОПРОСЫ
1.Можно ли достичь резонанса в изображенной на риc. В6.1 цепи изменяя: à) емкость конденсатора; á) приложенное к цепи напряжение; â) сопротивление резистора; ã) индуктивность катушки; ä) частоту приложенного к цепи напряжения?
2.Чему равно напряжение ULC на участке LC при резонансе?
3.Чему равна реактивная мощность в цепи при резонансе?
4.На каких участках цепи следует измерить напряжение для определения добротности?
5.(О) Увеличится или уменьшится полоса пропускания
цепи (риc. В6.1), если, сохраняя неизменной резонансную частоту, à) увеличить индуктивность; á) увеличить емкость; â) увеличить добротность контура; ã) увеличить емкость и одновременно уменьшить сопротивление r резистора; ä) увеличить сопротивление r резистора?
6. (О) Следует ли с целью уменьшения полосы пропускания цепи (риc. В6.1) при сохранении ее резонансной частоты: à) увеличивать волновое сопротивление и уменьшать
активное сопротивление; á) уменьшать индуктивность, Ðèc. Â6.1 увеличивая активное сопротивление?
7. Какое значение (наименьшее или наибольшее) принимает при резонансе напряжение на зажимах цепи (рис. В6.1) при питании ее от источника тока?
УПРАЖНЕНИЯ
1.Определите, как изменятся добротность контура, ток при резонансе и резонансная частота (риc. В6.1) при сохранении неизменными всех параметров и увеличении: à) сопротивления r â 1,5 ðàçà; á) индуктивности L â 2 ðàçà; â) емкости C â 3 ðàçà; ã) напряжения на входе в 2 раза?
2.(Р) В каком диапазоне частот входного напряжения U 220 B в контуре, име-
ющем резонансную частоту 00, с добротностью Q 20 и волновым сопротивлением 100 Ом ток будет превышать значение 31 А?
3.(Р) Напряжение UC на конденсаторе достигает при резонансе значения 1000 В, что недопустимо. Во сколько раз следует изменить емкость конденсатора, чтобы напряжение на нем снизилось на 10% при сохранении неизменной резонансной частоты?
4.(Р) Получите соотношение между частотами 01 è 02 изменения тока в цепи (риc. В6.1), при которых ее реактивные сопротивления равны по абсолютному значению, но противоположны по знаку.


 3. Покажем это. Обозначим через
3. Покажем это. Обозначим через 
 3 больше фазных, получаем
3 больше фазных, получаем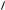

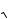
 2, òàê êàê ïðè ýòîì òîê
2, òàê êàê ïðè ýòîì òîê 
 15, .
15, . 
 2
2