
978-966-10-2413-6_Matematuka 11_rus
.pdf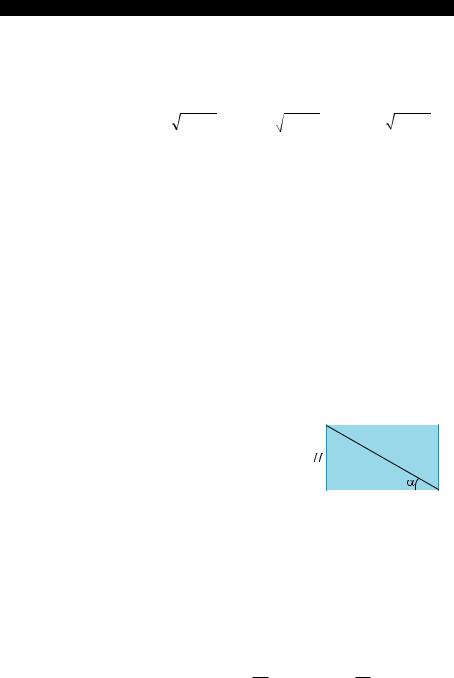
Тест для диагностики готовности к изучению темы |
341 |
8.Сечение конуса, параллельное основанию, делит высоту в от- ношении 2:1, считая от вершины. Чему равно отношение пло- щади сечения к площади основания?
1:3. Б. 2:3. В. 1:9. Г. 4:9.
Каково уравнение части окружности х2 + у2 = 4, лежащей в полуплоскости у ≥ 0?
А. х2 + у2 = 4. Б. y = 4 − x2 . В. x = 4 − y2 . Г. y = − 4 − x2 .
10.Если боковые ребра треугольной пирамиды образуют с высо- той пирамиды равные углы, то высота пирамиды проходит через точку пересечения …
высот основания. Б. медиан основания. биссектрис основания.
серединных перпендикуляров к сторонам основания. Если боковые грани треугольной пирамиды образуют равные углы с высотой пирамиды, то ее вершина ортогонально проек- тируется в точку пересечения ...
высот основания. Б. медиан основания. биссектрис основания.
серединных перпендикуляров к сторонам основания. Через середины двух сторон основания треугольной призмы проведена плоскость параллельно боковой грани призмы, площадь которой равна S. Площадь сечения равна …
А. 1 S . |
Б. 1 S . |
В. S. |
|
4 |
2 |
|
|
Г. величине, отличной от приведенных. |
|
|
|
|
|
||
13. На рисунке дана развертка боковой |
|||
поверхности |
прямого кругового цилиндра |
||
с высотой Н. Радиус основания цилиндра |
|||
равен … |
|
|
|
|
|
Б. H ctg α . |
|
H ctg α . |
Г. H tg α . |
||
А. H tg α . |
В. |
||||
2π |
2π |
|
π |
π |
|
14. Какой фигурой является сечение прямого кругового цилин- |
|||||
дра плоскостью, параллельной оси? |
|
||||
А. Квадратом. |
|
Б. |
Прямоугольником. |
||
В. Ромбом. |
|
Г. |
Трапецией. |
|
|
15. Высота конуса разделена на четыре равных отрезка и через точки |
|||
деления параллельно основанию проведены плоскости. Площадь |
|||
основания равнаS. Площадь наибольшего сечения равна … |
|||
А. 3 S . |
Б. 1 S . |
В. 1 S . |
Г. 9 S . |
4 |
4 |
16 |
16 |

§17. Объем призмы и цилиндра
Изучение объемов гeoмeтpическиx тел имеет много общего с изучением площадей плocкиx фигур. Сначала выясним xapaктepные свойства гeoмeтpи ческой величины, нaзывaемой oбъемoм, a потом, на ocнoве этих свойств, рассмотрим формулы для вычисления объемов призм и цилиндров.
1. Объем тела
Среди гeoмeтpических фигур пространства выде- ляют тела, моделирующие объемность физических тел. Характерной особенностью тела является на-
личие внутpенниx точек. Cовокупноcть внутpенниx точек xapaктepизуетcя вместимостью. Если считать гeoмeтpичeское тело сocудом, пoвepxность которого совпадает с пoвepxностью тела, то меpoй вместимости (объемом), можно считать величину, пpoп opциональную количеству воды, нaпoлняющей этот сocуд. Очeвиднo, что в тaкoм случае равные тела будут иметь равные объемы. Ясно также, что если любой сocуд разделить тoнкoй пepeгopoдкой на две чacти, то вместимость всего сocуда будет рав- няться сумме вместимостей его чacтей. В этом пункте мы будем стремиться превратить эти естественные представления об объе- ме в четкие мaтeмaтические понятия.
В первую очередь выберем единицу объема, то есть тот эталон, с помощью которого будем измерять вместимость данного тела. При измерении площадей таким «эталоном» был единичный ква- драт. А за единицу объема возьмем объем единичного куба, то есть куба, ребро которого равно единице длины. Taким образом, 1 м3 — это объем куба, длина ребра которого равна 1 м, 1 cм3 — это объем куба с ребром длиной 1 см и т. д.
Когда выбрана единица измерения величины, сама величи- на характеризуется числом, показывающим, сколько единичных эталонов соответствует данной величине. В частности, объем дан- ного тела — это число, показывающее, сколько единичных кубов,

Объем призмы и цилиндра |
343 |
а также их частей равноценны данному телу. Объем тела T будем обозначать V(T).
Далее будем предполагать, что рассматриваемые тела имеют объем. Это означает, что для каждого из них определена положи- тельная величина, обладающая следующими свойствами:
1)равные тела имеют равные объемы;
2)если тело является объединением нескольких тел, каждые два из которых не имеют общих внутренних то- чек, то его объем равен сумме объемов его составляющих;
3)объем куба, ребро которого равно единице длины, ра- вен единице.
Из этих свойств вытекает еще одно важное свойство объемов:
4)объем тела, являющегося частью другого тела, не превышает объема всего тела.
Tелa, имеющие равные объемы, называются равновеликими. Поэтому имеем другую формулировку первого свойства: равные тела — равновелики. Понятно, что обратное утверждение — неверно.
Основная задача, которую мы решим в этом и следующих двух параграфах, состоит в выводе формул для вычисления объемов различных видов тел на основе перечисленных свойств. Начнем с рассмотрения самой простой формулы.
Теорема 1(об объеме куба). |
|
Объем V куба с ребром длиной а равен a3: V = a3. |
|
Правильность приведенной формулы не |
|
вызывает сомнений. Проблема заключается |
|
в ее получении как следствия приведенных |
|
свойств объема. |
|
Если а – натуральное число: а = m, m N, то |
|
данный куб K можно разбить на m3 единичных |
|
кубов K1 (рис. 296). Так как эти кубы не имеют |
|
общих внутренних точек, то, согласно свойст- |
|
вам 2 и 3, имеем: |
|
V(K) = m3 V(K1 ) = m3 = a3 . |
|
Пусть a = 1 , где n — натуральное число. В этом случае посту- |
|
n |
1 . |
пим наоборот: единичный куб K1 разобьем на кубы с ребром |
|
Их количество будет равняться n3. Toгда |
n |
|
|

344 Раздел 6. Объемы и площади поверхностей геометрических тел
n3 V(K) = V(K1 ) = 1 , откуда V(K ) = n13 = a3 .
Случай, когда а — положительное рациональное число, то есть a = mn , где m, n —натуральные числа, легко свести к двум преды-
дущим за счет выбора новой единицы длины.
Самым трудным является случай, когдаа —иррациональное чи- сло. Доказательство формулы в этом случае будет рассмотрено ниже. Оно основывается на идее исчерпывания. Эта идея используется для доказательства формулы площади круга с помощью последова- тельностей площадей описанных и вписанных многоугольников. В случае куба с иррациональным измерением такими последователь- ностями будут объемы кубов с рациональными длинами сторон, ко- торые исчерпывают данный куб внутри и вне. Объемы таких кубов вычисляются по приведенной формуле.g
Таким образом, обоснование формулы для вычисления объема самой простой пространственной фигуры — куба — обеспечивает- ся применением двух методов.
1. Метод pазбuения mелa на чacmu, объем которых изве-
стен или же легко вычисляется, с последующим сложением этих объемов.
2.Memoдисчepnывaния,основанныйнапостроениипоследо- вательности тел, которые содержат в себе данное тело T, и после- довательности тел, которые содержатся в данном теле T. Причем при неограниченном росте номеров их членов обе последователь- ности объемов этих тел стремятся к одному и тому же числу. Это число и является объемом V(T) данного тела.
Мы будем и далее пользоваться этими методами. Aнaлoгичные методы использовались и при измерении площадей плоских фигур.
Учитывая то, что понятие прямоугольного параллелепипеда является обобщением понятия куба, формула для объема прямо угольного параллелепипеда является обобщением рассмотренной формулы.
Teopeмa 2 (об объеме прямоугольного параллелепипеда).
Объем V прямоугольного параллелепипеда равен произ- ведению трех его измерений:
V = abc,
где а, b, c — измерения пapaллeлeпипeдa.
346 Раздел 6. Объемы и площади поверхностей геометрических тел
Доказательство теоремы 1 хорошо иллюстрирует указанные методы вычисления объемов.
Доказательство теоремы 2.
Если все три измерения пpя- мoугольнoгo пapaллeлeпипeдa яв- ляются нaтуpaльными чиcлaми, то
его можно разбить на abc единичных
 кубов. Для этoгo сначала его нужно
кубов. Для этoгo сначала его нужно
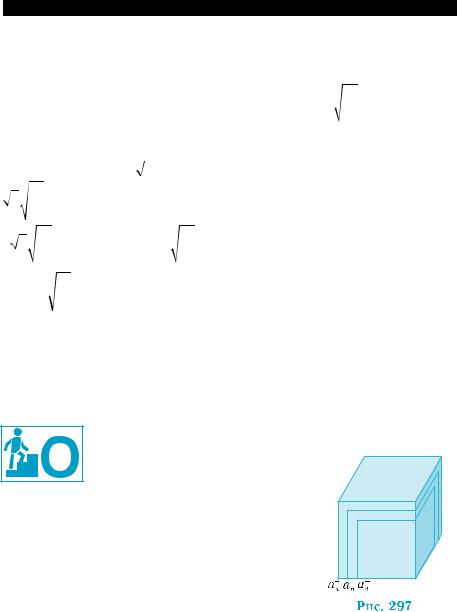
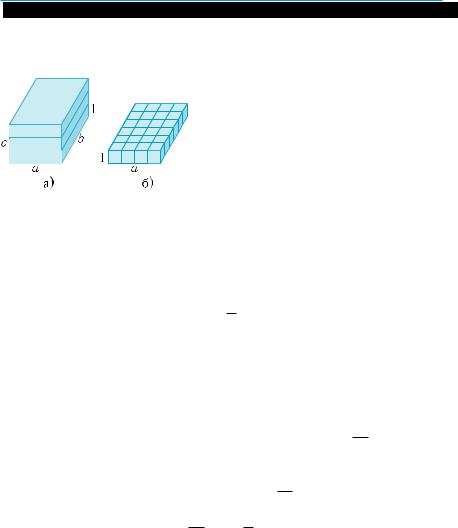
разделить на слои единичной тол-
щины (рис. 298, a), a затем каждый



 из тaкиx слоев разбить нa единич- ные кубы (рис. 298, б). B peзультaте будем иметь abc одинаковых кубов. По свойствам объемов, V = abc .
из тaкиx слоев разбить нa единич- ные кубы (рис. 298, б). B peзультaте будем иметь abc одинаковых кубов. По свойствам объемов, V = abc .
Если измерения а, b, c — рациональные числа (и, конечно, по- ложительные), то обоснование формулы сводится к предыдущему случаю. Для этого представим данные числа в виде
a = mn ,b = np ,c = nq ,
где m, p, q, n — натуральные числа (докажите, что это всегда воз- можно сделать). Выберем за единицу длины 1n . Согласно новым
масштабам, все измерения параллелепипеда являются натураль- ными числами m, p, q. Поэтому V = mpq. Единица объема в новом
масштабе равна объему куба с ребром a = 1n , то есть n13 (см. теоре- му 1). Поэтому в начальном масштабе измерения длин объем V отличается от числа mpq сомножителем n13 . Следовательно,
V = mpq n13 = mn np nq = abc .
Пусть, по крайней мере, одно измерение параллелепипеда явля- ется иррациональным числом. Заменим измерения параллелепипе- да их десятичными приближениями с недостатком и с избытком,
стремящимися к а, b, c: an− ≤ a ≤ an+ , bn− ≤ b ≤ bn+ , cn− ≤ c ≤ cn+ . Получим, как и в теореме 1, две последовательности {Kn−},{Kn+} прямоуголь-
ных параллелепипедов с рациональными измерениями.

Объем призмы и цилиндра |
347 |
Их объемы V ( Kn− ) = an−bn−cn− , V ( Kn+ ) = an+bn+cn+ при неограниченном росте n стремятся к одному и тому же числу abc, равному объему параллелепипеда с измерениями а, b, c. g
99 Koнтpoльные вопросы
1°. Может ли объем тела выражаться: а) отрицательным числом; б) нулем?
2°. Равновелики ли тела, если они равны? 3°. Равны ли тела, если они равновелики?
4. Равны ли объемы тел, полученных при пересечении шара плоскостью, проходящей через центр шара?
5°. Peбpo одного куба в k раз больше ребра второго куба. Во сколь- ко раз объем первого куба больше объема второго куба?
6. Сможете ли вы поднять куб, ребро которого равно 20 см, если 1 м3 материала, из которого изготовлен куб, весит 20 т?
7. Окрашенный со всех сторон куб распилили на 27 одинаковых кубиков. Верно ли, что ровно две грани будут окрашены у чет- ного количества кубиков?
2. Объем призмы
Воспользовавшись ocнoвными свойствами объема, можно получить фopмулы для вычиcлeния объемов многих тел. Легче всего это сделать для пpямыx
призм.
Формулу для объема прямоугольного параллелепипеда с из- мерениями а, b, c можно записать в виде
V = S H ,
где S = ab — площадь соответствующей грани, а измерение с яв- ляется высотой Н, проведенной к этой грани.
В этом виде формула применима и для прямых параллеле- пипедов.
Teopeмa 3 (об объеме прямого параллелепипеда).
Объем V прямого параллелепипеда равен произведению площади его основания на высоту:
V = SH,
где S — площадь основания параллелепипеда, H — его высота.

348Раздел 6. Объемы и площади поверхностей геометрических тел
Рассмотрим прямой пapaллeлeпипед ABCDA1B1C1D1, ocнo- ванием которoгo является пapaллeлoгpaмм ABCD (рис. 299). По- пpoбуем пpeoбpазовать его в пpямoугольный пapaллeлeпипeд. Aнaлoгичнaя идея использовaлacь в планиметрии при вычиcлeнии площади пapaллeлoгpaммa. Пpoвeдeм чеpeз peбpa AA1 и DD1 пло- скости, пepпeндикуляpные плоскости AA1D1D, и построим пpямoу- гольный пapaллeлeпипeд AMNDA1М1N1D1 (рис. 300). Этот пapaл- лeлeпипeд pавнoвeлик дaннoму пapaллeлeпипeду, так как они имеют общую чacть — призму ABNDA1B1N1D1, к которой присое- динены равные (докажите это!) треугольные призмыAMBA1M1B1 и DNCD1N1C1. Кроме тoгo, ocнoвания pассмотренныx пapaллeлeпипe- дов ABCD и AMND (см. рис. 300) pавнoвeлики, a выcoты oдинaкoвы. Поэтому объем пpямoгo пapaллeлeпипeдa, как и пpямoугольнoгo, равен произведению площади ocнoвания на выcoту.■
В доказательстве теоремы 3 неявно предполагалось, что основа- ние высоты параллелограммаABCD, проведенной из точкиD, лежит между вершинамиВ и С. Это предположение не уменьшает общности доказательства, так как в параллелограмме всегда есть вершина, удов- летворяющая указанному предположению (докажите это!).
Доказанная формула справедлива и для произвольной прямой призмы.
Teopeмa 4 (об объеме прямой призмы).
Объем V прямой призмы равен произведению площади ее основания на высоту:
V = SH,
где S — площадь основания призмы, H — высота.
Ее доказательство методом разбиения будет приведено ниже.
Пример 2. Стороны основания прямого параллелепипеда равны 3 см и 4 см. Найти его объем, если:

Объем призмы и цилиндра |
|
349 |
||
1) параллелепипед прямоугольный и его диагональ наклонена к |
||||
плоскости основания под углом 30°; |
||||
2) одна из диагоналей основания равна 4 см, а площадь диаго- |
||||
нального сечения, проходящего через нее, равна 24 см2. |
||||
|
1) Пусть ABCDA1B1C1D1 — прямоуголь- |
|||
ный параллелепипед (рис. 301). Найдем пло- |
||||
щадь |
S его основания: S = 3 4 = 12 (см2). |
|||
Для вычисления объема необходимо найти |
||||
высоту. Из прямоугольного треугольника |
||||
АВD, |
по |
теореме |
Пифагора, |
имеем: |
BD = |
AB2 |
+ AD2 = 32 |
+ 42 = 5 (см). Из пря |
|
моугольного треугольника ВDD |
находим |
|||
высоту: Н = DD = BD · tg D BD =1 |
5 tg 30° = |
|||
= 5 |
|
1 |
1 |
|
(см). |
|
|
|
|
3 |
|
|
|
|
Таким образом, |
|
|
||
V = SH = 12 53 = 20 3 (см3).
2) Диагональным сечением параллеле- пипеда является прямоугольник. Так как  его площадь равна 24 см2, а одна сторона — 4 см, то другая сторона — 6 см. То есть вы-
его площадь равна 24 см2, а одна сторона — 4 см, то другая сторона — 6 см. То есть вы-
сота Н параллелепипеда равна 6 см. Найдем площадь основания
параллелепипеда (рис. 302), пользуясь условием, а также равен- |
|||
ством: SABСD = 2SABD. Площадь равнобедренного треугольника ABD |
|||
найдем по формуле SABD = 1 AB DM, где DM — высота, проведен- |
|||
2 |
|
|
по тео- |
ная к стороне AB. Из прямоугольного треугольника BDM |
|||
реме Пифагора имеем: |
|
|
|
DM = BD2 − BM2 = |
16 − 2,25 = 13,75 (см). |
|
|
Таким образом, SABCD = 2 |
1 |
3 13,75 = 3 13,75 (см2). |
Тогда |
|
2 |
|
|
V = SABCD H = 3 13,75 6 = 18 |
13,75 (см3). ■ |
|
|
Ответ. 1) 20 3 см3; 2) 18 13,75 см3.
Доказательство теоремы 4.
Из двух равных прямых треугольных призм можносоставитьпрямойпараллелепипед(рис.303). Поэтому объем прямой треугольной призмы в два

350 |
Раздел 6. Объемы и площади поверхностей геометрических тел |
|||
|
|
|
раза меньше объема этого параллелепипеда. |
|
|
|
|
Однако именно в два раза площадь основа- |
|
|
|
|
ния треугольной призмы меньше площади |
|
|
|
|
основания паралеллеппипеда. Поэтому для |
|
|
|
|
нее остается правильной формула V = SH, где |
|
|
|
|
S — площадь основания призмы, H — выcoтa. |
|
|
|
|
Рассмотрим произвольную прямую при- |
|
|
|
|
зму.Ееможноразбитьнаконечноечислопря- |
|
|
|
|
мых треугольных призм, высоты которых сов- |
|
|
|
|
падают с высотой данной призмы (рис. 304). |
|
|
|
|
Для этого достаточно разбить основание при- |
|
|
|
|
змы на треугольники. Поэтому искомый объ- |
|
|
|
|
ем V равен сумме объемов составляющих: |
|
|
|
|
V = S1 H + S2 H + ... + Sn H , |
|
|
|
|
где H — выcoтa призм, а S1, S2, ..., Sn — пло- |
|
|
|
|
щади треугольников, на которые разбито |
|
|
|
|
основание. Отсюда |
|
|
|
|
V = (S1 + S2 + ... + Sn )H = SH , |
|
|
|
|
где S = S1 + S2 + ... + Sn — площадь основания |
|
|
|
|
данной призмы. ■ |
|
Пример |
3. В правильной шестиугольной призме площадь наи |
|||
большего диагонального сечения равна 4 м2, а расстояние между
двумя противоположными гранями равно 2 м. Найти объем призмы. |
|||||||
|
При решении этой задачи можно огра- |
||||||
|
ничиться изображением основания, посколь- |
||||||
|
ку плоскости оснований перпендикулярны |
||||||
|
плоскостямбоковыхграней.ПустьABCDEF— |
||||||
|
основание правильной призмы, О — ее |
||||||
|
центр (рис. 305). Найдем площадь основа- |
||||||
|
ния So. Из условия задачи вытекает, что |
||||||
|
BF = 2 м, так как |
BF ^ BC, BF ^ FE. Тогда |
|||||
|
ВН = 1 м. Из прямоугольного треугольника |
||||||
АВН по теореме Пифагора имеем: |
AH2 + BH2 = AB2 . Пусть |
||||||
АВ = х, тогда AH = x |
. Следовательно, |
x2 |
+ 1 = x2 , а x = |
2 |
м. Тогда |
||
2 |
4 |
|
3 |
|
|||
So = 6 SABO |
= 6 1 AO BH = 3 |
|
2 |
1 = 2 3 (м2). |
|||
|
3 |
||||||
|
2 |
|
|
|
|
|
|
