
Учебники / Hearing - From Sensory Processing to Perception Kollmeier 2007
.pdf48 |
S. Bandyopadhyay et al. |
Figure 3 shows the steps in computing an optimum shape. The left column shows the first iteration step. The initial reference q was an RSS stimulus with 0 dB in all bins, shown by the horizontal line in Fig. 3A. The dashed line shows an example of an RSS perturbation δ q. The eigenvector emax is shown in Fig. 3C and the discharge rates for stimuli with spectral shape q + Aemax are shown in Fig. 3E, plotted as a function of A. The open circle shows the rate in response to the 0-dB reference stimulus and the filled circle shows the maximum rate, over the 16-dB range tested. The error bars are the SD of 10 repetitions of each stimulus.
The second column shows the second iteration. The reference in this case (solid line in Fig. 3A) has the shape of emax from the first iteration. emax and
the rates for δ q = Aemax are shown in Fig. 3C,E as before. In this case the maximum rate occurred at the spectral shape shown in Fig. 3B. This stimulus is a
rate maximum for all directions δ q and so terminated the iterations.
Close inspection shows that the maximum rate after the second iteration was slightly smaller than the maximum rate after the first iteration. This occurred because of a systematic rate change in the neuron, sometimes seen in DCN principal cells. Essentially the rate decreased by 18% during the first iteration, as shown by rates in response to a control stimulus (not shown). Thus the rate maximum after the second iteration was indeed an overall rate maximum at this time.
The optimization process only constrains the amplitudes at frequencies to which the neuron is sensitive. The bins marked by asterisks in Fig. 3B account for 80% of the rate change across a set of RSS stimuli. Those are also the bins that changed significantly during the iteration; note that the remaining, nonasterisk, bins stayed near their initial values. Thus the optimal stimulus should be considered to consist of the four asterisked bins.
4The Optimal Stimulus for DCN Neurons
The optimal stimulus for the example neuron in Fig. 3B is a rising spectral slope centered on BF. Figure 3D shows the outcome of the optimization process for a second type IV neuron, whose optimal stimulus is a sharp spectral edge at BF. The results of the optimization process thus correspond to the organization of excitatory and inhibitory inputs in Fig. 1 and the rate peaks observed in Fig. 2. It is important to emphasize that not all DCN principal cells show the notch edge sensitivity of the examples shown here, presumably because of different arrangements of the inhibitory inputs (Reiss and Young 2005).
The method of Sect. 3 provides a general way to find optimal spectral shapes that is applicable to neurons in all parts of the auditory system. It is fast and can be made faster by initiating the search with a reference stimulus that produces the highest discharge rate across an RSS set. Its major limitation is that it does not incorporate temporal aspects of the stimulus.
Acknowledgements. This work was supported by NIH grants DC00115 and DC05211.
Spectral Edges as Optimal Stimuli for the Dorsal Cochlear Nucleus |
49 |
References
Blum JJ, Reed MC (1998) Effects of wide band inhibitors in the dorsal cochlear nucleus. II. Model calculations of the responses to complex tones. J Acoust Soc Am 103:2000–2009
Cover TM, Thomas JA (1991) Elements of information theory. Wiley-Interscience, New York Davis KA, Miller RL, Young ED (1996) Effects of somatosensory and parallel-fiber stimulation
on neurons in dorsal cochlear nucleus. J Neurophysiol 76:3012–3024
deCharms RC, Blake DT, Merzenich MM (1998) Optimizing sound features for cortical neurons. Science 280:1439–1443
Eggermont JJ, Aertsen AMHJ, Johannesma PIM (1983) Prediction of the responses of auditory neurons in the midbrain of the grass frog based on the spectro-temporal receptive field. Hearing Res 10:191–202
Johnson DH, Gruner CM, Baggerly K, Seshagiri C (2001) Information-theoretic analysis of the neural code. J Comput Neurosci 10:47–69
Kanold PO, Young ED (2001) Proprioceptive information from the pinna provides somatosensory input to cat dorsal cochlear nucleus. J Neurosci 21:7848–7858
Machens CK, Wehr MS, Zador AM (2004) Linearity of cortical receptive fields measured with natural sounds. J Neurosci 24:1089–1100
May BJ (2000) Role of the dorsal cochlear nucleus in the sound localization behavior of cats. Hearing Res 148:74–87
Middlebrooks JC (1992) Narrow-band sound localization related to external ear acoustics. J Acoust Soc Am 92:2607–2624
Nelken I, Young ED (1994) Two separate inhibitory mechanisms shape the responses of dorsal cochlear nucleus type IV units to narrowband and wideband stimuli. J Neurophysiol 71:2446–2462
Nelken I, Kim PJ, Young ED (1997) Linear and non-linear spectral integration in type IV neurons of the dorsal cochlear nucleus: II. Predicting responses using non-linear methods. J Neurophysiol 78:800–811
O’Connor KN, Petkov CI, Sutter ML (2005) Adaptive stimulus optimization for auditory cortical neurons. J Neurophysiol 94:4051–4067
Reiss LAJ, Young ED (2005) Spectral edge sensitivity in neural circuits of the dorsal cochlear nucleus. J Neurosci 25:3680–3691
Rouiller EM (1997) Functional organization of the auditory pathways. In: Ehret G, Romand R (eds) The central auditory system. Oxford University Press, New York, pp 3–96
Shore SE (2005) Multisensory integration in the dorsal cochlear nucleus: unit responses to acoustic and trigeminal ganglion stimulation. Eur J Neurosci 21:3334–3348
Voigt HF, Young ED (1990) Cross-correlation analysis of inhibitory interactions in dorsal cochlear nucleus. J Neurophysiol 64:1590–1610
Young ED, Calhoun BM (2005) Nonlinear modeling of auditory-nerve rate responses to wideband stimuli. J Neurophysiol 94:4441–4454
Young ED, Davis KA (2001) Circuitry and function of the dorsal cochlear nucleus. In: Oertel D, Popper AN, Fay RR (eds) Integrative functions in the mammalian auditory pathway. Springer, Berlin Heidelberg New York, pp 160–206
Yu JJ, Young ED (2000) Linear and nonlinear pathways of spectral information transmission in the cochlear nucleus. PNAS 97:11780–11786
Comment by Langner
According to your Fig. 1 the spectral notches in cat head-related transfer functions show up around 10 kHz, which would suggest a functional role for units with an inhibitory area close to or at their CF around 10 kHz. However,
50 |
S. Bandyopadhyay et al. |
the tuning curves of type IV neurons are similar not only around 10 kHz but for all center frequencies. Therefore my question is: What is your opinion about the functional role of type IV neurons outside the 10-kHz range?
Reply
We have noted previously that type IV neurons with notch sensitivity do not seem to be limited to BFs where the cat’s ear shows spectral notches (Young and Davis 2001, Fig. 5.13). The present chapter, along with the results of Lina Reiss (Reiss and Young 2005), provide an alternative view of DCN notch sensitivity as sensitivity to rising frequency edges. During the meeting, an interesting suggestion was made by B. Delgutte: because the acoustic environment is usually low-pass in its spectral content, DCN neurons may be tuned to unusual acoustic features which are high-pass, by contrast to the usual spectra. This corresponds well to our previous suggestions that the DCN may serve to detect potentially important acoustic events and report them to the auditory system (Nelken and Young 1996).
References
Nelken I, Young ED (1996) Why do cats need a dorsal cochlear nucleus? Rev Clin Basic Pharmacol 7:199–220
Reiss LAJ, Young ED (2005) Spectral edge sensitivity in neural circuits of the dorsal cochlear nucleus. J Neurosci 25:3680–3691
Young ED, Davis KA (2001) Circuitry and function of the dorsal cochlear nucleus. In: Oertel D, Popper AN, Fay RR (eds) Integrative functions in the mammalian auditory pathway. Springer, Berlin Heidelberg New York, pp 160–206

7 Psychophysical and Physiological Assessment of the Representation of High-frequency Spectral Notches in the Auditory Nerve
ENRIQUE A. LOPEZ-POVEDA1, ANA ALVES-PINTO1, AND ALAN R. PALMER2
1Introduction
Destructive interference between sound waves within the pinna produces notches in the stimulus spectrum at the eardrum. Some of these notches have a center frequency that depends strongly on the relative vertical angle between the sound source and the listener (e.g. Lopez-Poveda and Meddis 1996). Therefore, it is not surprising that they constitute useful cues for judging sound source elevation (reviewed by Carlile et al. 2005).
The auditory nerve (AN) is the only transmission path of acoustic information to the brain. Single fibers encode the physical characteristics of the sound in at least two ways: in their discharge rate and in the time at which their spikes occur (reviewed by Lopez-Poveda 2005). Because spectral notches due to the pinna occur at frequencies beyond the cut-off of phase locking, the common view is that the AN representation of these notches must be based on the discharge rate alone, i.e. temporal representations do not contribute (Rice et al. 1995). In other words, the brain would infer the stimulus spectrum from a representation of the discharge rate of the population of AN fibers as a function of their characteristic frequencies (CFs). This representation is known as the rate profile.
On the other hand, evidence exists that the apparent quality of the rateprofile representation of high-frequency spectral notches degrades as the sound pressure level (SPL) of the stimulus increases (Rice et al. 1995; LopezPoveda 1996). Almost certainly this is due to the low threshold and the narrow dynamic range of AN fibers with high-spontaneous rate (HSR), which are the majority, and to the progressive broadening of their frequency tuning with increasing SPL. Although low-spontaneous rate (LSR) fibers have higher thresholds and wider dynamic ranges, they are a minority. Furthermore, the broadening of basilar membrane tuning at high levels makes it unlikely that they can convey high-frequency spectral notches in their rate profile equally well at low and high levels (Carlile and Pralong 1994; Lopez-Poveda 1996).
1Instituto de Neurociencias de Castilla y León, Universidad de Salamanca, Avda. Alfonso X El Sabio s/n, 37007 Salamanca, Spain, ealopezpoveda@usal.es, aalvespinto@usal.es
2MRC Institute of Hearing Research, University Park, Nottingham, NG7 2RD, UK, alan@ihr.mrc.ac.uk
Hearing – From Sensory Processing to Perception
B. Kollmeier, G. Klump, V. Hohmann, U. Langemann, M. Mauermann, S. Uppenkamp, and J. Verhey (Eds.) © Springer-Verlag Berlin Heidelberg 2007
52 |
E.A. Lopez-Poveda et al. |
Consistent with this, one would expect that to discriminate between a flatspectrum noise and a similar noise with a spectral notch centered at a high frequency (say 8 kHz) would be increasingly more difficult as the overall stimulus level increases. However, contrary to this expectation we have shown (Alves-Pinto and Lopez-Poveda 2005) that the ability to discriminate between flat-spectrum and notched noise stimuli is a nonmonotonic function of level for the majority of listeners. Specifically, discrimination is more difficult at levels around 70–80 dB SPL than at lower or higher levels.
Here we report on our efforts at understanding the nature of this paradoxical result. Our approach consists in predicting the limits of psychophysical performance in the spectral discrimination task of Alves-Pinto and Lopez-Poveda (2005) based on the statistical analysis of experimental AN responses. The results contradict the common view that high-frequency spectral notches are conveyed to the central auditory system in the AN rate profile. Instead, they suggest that spike rates over narrow time windows almost certainly convey useful information for discriminating between noise bursts with and without high-frequency spectral notches.
2Methods
The activity of guinea pig AN fibers was recorded in response to the same bursts of broadband (20–16,000 Hz) frozen noise that we used in our previous psychophysical study. Two types of noise were considered. One had a completely flat spectrum while the spectrum of the other had a rectangular notch between 6000 and 8000 Hz with a depth of 3 dB re. noise spectrum level. Responses were measured for overall noise levels between 40 and 100 dB SPL in steps of 10 dB. The noise bursts had a duration of 110 ms, including a 10-ms rise ramp (no fall ramp was applied), and were presented every 880 ms. Details on the noise generation procedure are given elsewhere (Alves-Pinto and Lopez-Poveda 2005).
Responses were recorded for a sample of 106 AN fibers (from 16 animals) with CFs spanning a range from 1000 to 19,000 Hz. Of the fibers, 31 had spontaneous rates less than 18 spikes/s. The method of recording of physiological responses was virtually identical to that described in Palmer et al. (1985). The response of any given fiber was measured at least five times for each stimulus condition.
2.1Statistical Analysis of Auditory Nerve Responses
The psychophysical just-noticeable difference (JND) in a given stimulus parameter, ∆αJND, can be predicted from the instantaneous discharge rate of the population of AN fibers as follows (Siebert 1970; Heinz et al. 2001):
|
|
|
|
|
- 0.5 |
|
|
DaJND= */ |
T |
1 |
< |
2ri (t, a) |
2 dt 4 , |
(1) |
|
#0 |
ri (t, a) |
2a |
|||||
i |
F |
|
Psychophysical and Physiological Assessment |
53 |
where t denotes time, and ri(t, α) the instantaneous discharge rate of the i-th fiber in response to the stimulus with parameter α. In our context, α corresponds to the notch depth. Hence, Eq. (1) allows predicting the threshold notch depth for discriminating between a flat-spectrum noise and a noise with a spectral notch based on the experimental AN responses.
Equation (1) was derived on the assumption that the times at which AN spikes occur follow a Poisson distribution (i.e., that spikes occur at times that are independent of each other). Furthermore, it was derived on the assumption that psychophysical discrimination thresholds reflect optimal use of every bit of information available in the activity of the population of fibers. Neither of these two conditions apply here (see Heinz et al. 2001); thus we do not expect the resulting ∆αJND values to match the psychophysical thresholds directly. However, it is reasonable to assume that the error in using Eq. (1) for predicting the psychophysical thresholds will be similar for all SPLs. Therefore, Eq. (1) remains useful for predicting the shape of the threshold notch depth vs level function, as reported previously by us (Alves-Pinto and Lopez-Poveda 2005).
It is noteworthy that Eq. (1) predicts the threshold notch depth for spectral discrimination using the instantaneous discharge rate of the population of AN fibers. This contrasts with the rate-place model described in the Introduction that only considers the information conveyed in the overall discharge rate of the fibers.
For obvious reasons, in applying Eq. (1) we had to consider a discrete version of the instantaneous discharge rate, ri(∆t, α) rather than the continuoustime ri(t, α). Note that ri(∆t, α) may be interpreted as a mean-rate post-stimulus time histogram for a bin width duration of ∆t. Instead of decid-
ing on an arbitrary value for ∆t, we computed ∆αJND for different bin widths (or sampling periods), ∆t, from 0.333 to 110 ms. Note that in the extreme case
that ∆t equals the stimulus duration, the resulting ∆αJND corresponds to performance based on a rate-place code only.
In Eq. (1), the term between square brackets denotes the change in instantaneous discharge rate for an incremental change in parameter α. It was calculated as the instantaneous difference in discharge rate for the
flat-spectrum, (α = 0 dB) and the notched (α = 3 dB) noises. ∆αJND becomes unrealistically equal to zero when the discharge rate of any fiber is equal to
zero for any bin. To prevent this artifactual result, a small, arbitrary constant of 0.1 spikes/s was added to the measured discharge rate in all bins of all fibers. The actual value of this constant did not alter the results significantly.
3Results
The results are illustrated in Fig. 1. The series denoted by the open circles (left ordinate) illustrates the ∆αJND values based on the experimental AN responses. These will be hereinafter referred to as the physiological JNDs.
54 |
E.A. Lopez-Poveda et al. |
1 |
|
|
|
|
|
100 |
|
110 ms |
|
|
|
|
|
|
|
55 |
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
Psychophysical JND (dB) |
0.1 |
|
|
|
|
|
10 |
|
|
|
|
|
S1 |
8 |
|
|
9 |
|
|
|
|
|
||
|
|
|
|
|
|
||
PhysiologicalJND(dB) |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
||
4 |
|
|
|
|
|
|
|
0.01 |
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
0.005 |
|
|
|
|
|
0.5 |
|
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
Level (dB SPL)
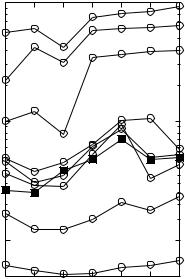
Fig. 1 Predicted threshold notch depth values from auditory nerve responses (circles, left ordinate) for different bin widths (as denoted by the numbers next to each trace). Also shown for comparison is an example psychophysical function (squares, right ordinate) taken from AlvesPinto and Lopez-Poveda (2005)
Each series illustrates the results for a different bin width, ∆t, as indicated by the numbers next to each trace. The series denoted by filled squares (right ordinate) illustrates a particular example of a psychophysical threshold notch depth vs level function taken from Alves-Pinto and Lopez-Poveda (2005; Fig. 3, listener S1). Notice that the scales of both ordinate axes are logarithmic (after Alves-Pinto and Lopez-Poveda 2005) and span a comparable range of values in relative terms, but not in absolute terms.
In general, for any given SPL, the physiological-JND values increase as the sampling period ∆t increases, suggesting that discrimination benefits from the information conveyed by the timing of spike occurrences.
The most striking result is that the shape of the physiological-JND vs level functions varies largely depending on the time window ∆t. Only for ∆t values within the range from 4 to 9 ms are the physiological-JND functions nonmonotonic with a peak at or around 80 dB SPL, thus resembling the shape of the psychophysical threshold notch depth vs level function (squares). In absolute terms, however, the physiological-JND values are about two orders of magnitude lower than the psychophysical ones (for the listener considered in Fig. 1). This may reflect differences in cochlear
Psychophysical and Physiological Assessment |
55 |
processing between human and guinea pig, and/or that humans do not behave as “optimal” spectral discriminators; otherwise the absolute values would match.
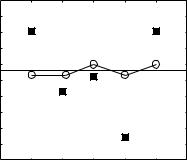
The shape of the psychophysical threshold notch depth vs level function varies among listeners (Alves-Pinto and Lopez-Poveda 2005). Similarly, the shape of the physiological-JND vs level function depends on the value of the bin width ∆t (Fig. 1). Kendall’s τ correlation coefficient (Press et al. 1992) was used to quantify the degree of correlation between the shapes of the psychophysical function for each one of five listeners (S1 to S5) considered by Alves-Pinto and Lopez-Poveda (2005) with the physiological-JND vs level functions for different values of ∆t. Figure 2 shows the ∆t values (circles; left ordinate) that yielded the highest correlations for each listener, as well as the corresponding correlation values (squares; right ordinate). The degree of correlation varies considerably across listeners, but the ∆t that yields the highest correlations is similar across listeners (mean ± s.d. =8.66 ± 0.36).
In Fig. 1, the series for ∆t equal to the stimulus duration (110 ms, top trace), shows the predicted physiological-JND values taking only the overall average discharge rate. The shape of this function clearly differs from that of the psychophysical function and matches overall the prediction of the rate-only theory. That is, threshold notch depths are lowest for overall levels around 60 dB SPL (corresponding to a spectrum level of 18 dB SPL) and increase progressively with increasing SPL. The level for which the physiological-JND is
Best binwidth (ms)
13 |
|
|
|
12 |
** |
** |
|
11 |
|||
|
|
10
9
8
7
6
5
4
3
S1 S2 S3 S4 S5
Listener
1 |
binwidth |
|
0.8 |
||
bestfor |
||
0.6 |
||
|
||
0.4 |
Correlation |
|
0.2 |
||
|
||
0 |
|
Fig. 2 Binwidths (circles, left ordinate) for which maximum correlation occurred between the shapes of the physiological and the psychophysical threshold notch depth vs level functions for the five listeners considered by Alves-Pinto and Lopez-Poveda (2005). Squares (right ordinate) illustrate the actual degree of correlation. Two asterisks denote highly significant ( p < 0.01) correlations
56 |
E.A. Lopez-Poveda et al. |
|
0.4 |
|
|
|
|
|
|
JND (dB) |
0.3 |
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
0.1 |
|
|
|
|
|
|
|
Physiological |
|
|
|
|
HSR |
|
|
|
|
|
|
LSR |
|
|
|
|
|
|
|
HSR+LSR |
|
||
|
|
|
|
|
|
||
|
0.01 |
|
|
|
|
|
|
|
40 |
50 |
60 |
70 |
80 |
90 |
100 |
Level (dB SPL)
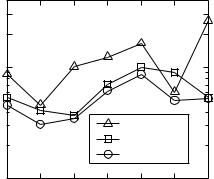
Fig. 3 Physiological JND (in dB) vs SPL based on the information conveyed by fiber groups of different types
lowest corresponds to an effective level of approximately 28 dB SPL (assuming a fiber with a CF = 8000 Hz and an effective bandwidth of 1000 Hz), which approximately falls at the center of the dynamic range of HSR fibers.
Figure 3 compares the physiological-JND vs level function (for ∆ t = 8.33 ms) for three cases: using the information conveyed by all 106 fibers (circles) – this is the case considered so far; using only the information conveyed by the 75 fibers with SRs≥18 spikes/s (HSR, triangles); and using only the information from the 31 fibers with SRs<18 spikes/s (LSR, squares). Differences exist between the functions. Nonetheless, the physiological JND is a nonmonotonic function of SPL in all three cases and a peak occurs at 80 dB SPL.
4Discussion
We have previously suggested that the nonmonotonic aspect of the psychophysical threshold notch depth vs level function reflects the existence of two fiber types (HSR and LSR) with different thresholds and dynamic ranges (Alves-Pinto and Lopez-Poveda, 2005; Alves-Pinto et al. 2005), and that the peak around 80 dB SPL indicates the transition between their dynamic ranges. This interpretation is, however, almost certainly wrong as the predicted threshold notch depth vs level function is nonmonotonic with a peak at 80 dB SPL even when the two types of fibers are considered separately (Fig. 3).
Psychophysical and Physiological Assessment |
57 |
Our previously suggested interpretation was based on the premise that the spectral notch must be encoded in the AN rate profile. The present results suggest that this premise is almost certainly false.
Indeed, the results of Fig. 1 argue against the view that high-frequency spectral notches must be encoded in the average rate profile of AN fibers and suggest, instead, that the discharge rate over narrow time windows conveys useful information for discriminating between flat-spectrum and notched noise stimuli. The results also suggest that humans somehow sample the discharge rate of AN fibers in non-overlapping time windows of approximately 8.6 ms (Fig. 2).
Three important questions arise now: 1) what is the temporal code in question; 2) how is it generated; and 3) how does it relate to the predicted 8.6-ms sampling period. The answer to these questions requires further analysis of the AN responses and we can only speculate at present.
The effective drive to any AN fiber is a half-wave rectified, low-pass filtered version of the basilar membrane (BM) response waveform at its corresponding place in the cochlea. With broadband noise stimulation, this can be described as a randomly amplitude-modulated carrier with a carrier frequency near the fiber’s CF, where the range of modulation frequencies is limited by the bandwidth of the cochlear filter (Louage et al. 2004) or the cut-off of phase locking. The bandwidth of BM filters, and thus the range of modulation frequencies, increases with increasing the SPL. Similarly, the phase of the BM response waveform depends on the filter bandwidth and thus on the stimulus SPL. AN fibers can phase-lock to the envelope of BM excitation even at high levels, when their discharge rate is at saturation (Cooper et al. 1993). Fibers with CFs near the notch frequency certainly “see” a different level compared with those with CFs well away from it. It is, therefore, possible that spectral discrimination be based on detecting either the range of modulation frequencies or the phase differences implicit in AN spike trains (or both).
On the basis of this conjecture, the psychophysical threshold notch depth vs level functions reported by Alves-Pinto and Lopez-Poveda (2005) would reflect the “dynamic range” of envelope-following rather than of discharge rate of AN fibers.
5Conclusions
High-frequency spectral notches are not encoded in the auditory rate profile, as is commonly thought. Instead, they are encoded by mean rate measures taken over quite short (~8.6 ms) time windows.
Acknowledgments. Work supported by FIS (PI02/203 and G03/203) and PROFIT (CIT-390000- 2005-4). We thank Trevor Shackleton, Ray Meddis, and Gerald Langner for their support and suggestions.
