Учебники / Hearing - From Sensory Processing to Perception Kollmeier 2007

2.3Analyses

Spikes were analysed using a 50-ms windowed segment of the response with the analysis window slid in 12.5-ms steps. From these windowed spike train segments we calculated an all-order interspike interval distribution between pairs of non-identical sweeps. Such shuffled all-order interval histograms (referred to as shuffled autocorrelograms (SAC)) have been used previously to show temporal responses to broadband noise in auditory nerve fibres (Louage et al. 2004).

3Results

The preliminary results reported in this paper come from the responses of 67 units in the VCN (8 Primary-Like, 15 Transient Chopper, 29 Sustained Chopper, 6 Onset (On-I and On-L) and 9 Low-BF phase-locking units). In most cases a range of frequency sweeps were played. Examples from three units are shown below. The plots show windowed normalised SAC functions.

In Fig. 2 we show the responses of a low-BF unit to a harmonic complex sweep with an F0 transition from 100 to 200 Hz over 500 ms. There is a clear peak in panel A at delays corresponding to the F0 throughout the response. There are also obvious peaks at shorter delays corresponding to delays appropriate for the second and third harmonics. The unit BF is 352 Hz; thus initially the third harmonic of the 100 to 200-Hz sweep would be dominant within the unit’s filter, with the second harmonic rapidly taking over as the dominant component. Approximately mid-way through the response the unit seems to respond predominantly to the fundamental component. With increasing levels of reverberation (Fig. 2B–D) the temporal representation of the stimulus remains clearly visible as peaks in the SAC, although the response to the third and second harmonics appears to be spread to later time points. We have observed similar responses from nine units with BFs in the range 200–500 Hz.

The responses of a Transient Chopper unit (BF = 2.34 kHz) are shown in Fig. 3. Again there is a clear representation of the stimulus in the dry condition, with peaks in the SAC corresponding to the stimulus fundamental. The peaks become much sharper as the stimulus periodicity enters this unit’s range of preferred periodicities. The BF of this unit is 2.34 kHz; hence it is responding to envelope periodicity resulting from beating between several unresolved harmonics within the peripheral filter. There is still a representation of the F0 transition in the 32-cm condition, although at 125 cm and 500 cm this representation has disappeared with the SACs tending towards unity, indicating the presence of uncorrelated spike times. This response pattern is typical of our population of units of all response types (except Onset- I) with BFs above approximately 1 kHz.

Low frequency Phase-locking unit (1270011)

BF = 352 Hz

Left: SACs

Binwidth = 50 s

Below: PSTH Binwidth = 0.2 ms

250 presentations of a 50-ms tone at BF, 50 dB above unit threshold

Fig. 2 Windowed normalised SACs of the response to a harmonic complex sweep with F0 100–200 Hz from a Low-BF unit: A the response to the dry stimulus and panels; B–D responses to the same stimulus after convolution with impulse responses at source-to-receiver distances as indicated in each panel. The scale along the ordinate in each case indicates the time through the stimulus.

The responses from a unit classified as Onset-I are shown in Fig. 4. This unit exhibits an almost perfect representation of the F0 transition in the dry condition. However, the addition of even very mild reverberation (32 cm) results in the almost complete abolition of a driven response. By 500 cm the raster plots in Fig. 4B show only spikes at stimulus onset. We have observed two units classified as On-I with this response pattern. Onset-L units give responses similar to those shown for the transient chopper neuron in Fig. 3.

4Discussion

We have shown that units responding to low-numbered resolved harmonics (Fig. 2) maintain a representation of the F0 in their interspike intervals even with relatively severe reverberation. In contrast the same representation in units responding to envelope modulation appears to be degraded with even relatively mild reverberation.

The breakdown of the temporal response in high frequency channels is likely due to the randomisation of the phase relationships between unresolved partials of the complex. This is further supported by the fact that low frequency channels showing responses to resolved components appear more resistant to the effects of reverberation with the main effect in these units being due to the smearing of the acoustic spectrum through time. Our On-I units’ responses to the reverberant conditions are similar to those in response to random phase harmonic complexes (Evans and Zhao 1998).

A major attraction of temporal theories of pitch processing (based largely on the autocorrelation approach) is that the same neuronal operation (i.e. counting of coincidences) applies equally well for both resolved and unresolved partials of a complex. Others have argued for a two-mechanism hypothesis, invoking some pattern recognition scheme for resolved regions and temporal processing for unresolved regions (e.g. Shackleton and Carlyon 1994). Despite the wealth of psychophysical evidence concerning the perception of vowels and other speech sounds under reverberant conditions, no study to our knowledge has specifically addressed the issue of the effect of reverberation on pitch perception when listening to either resolved or unresolved harmonics.

Our results suggest that in the presence of reverberation the use of temporal information may be limited to frequency channels containing resolved harmonics. These results are interesting in light of psychophysical evidence that in the presence of reverberation and a modulated F0 contour listener’s ability to perceptually segregate two competing sound sources with different F0s is compromised. In order to segregate sounds on the basis of an F0 difference it is necessary for a central processor to estimate the pitch of at least one of the competing sources, in order to either enhance the target sound, or to cancel the interfering sound (de Cheveigné et al. 1995). Based on our results it seems likely that if the listener is making use of higher, unresolved, harmonics to estimate the pitch of the interfering sound in the presence of reverberation, the cancellation of this sound would be difficult.

Ackowledgements. This work was supported by the BBSRC and the Wellcome Trust. We thank the Frank Edward Elmore and James Baird funds of the Cambridge MB/PhD programme for supporting one of the authors, MS.

References

Bleeck S, Sayles M, Ingham NI, Winter IM (2006) The time course of recovery from suppression and facilitation from single units in the mammalian cochlear nucleus. Hear Res 212:176–184 Culling JF, Summerfield Q, Marshall DH (1994) Effects of simulated reverberation on the use of binaural cues and fundamental-frequency differences for separating concurrent vowels.

Speech Commun 14:71–95

de Cheveigné A, McAdams S, Laroche J, Rosenberg M (1995) Identification of concurrent harmonic and inharmonic vowels: a test of the theory of harmonic cancellation and enhancement. J Acoust Soc Am 97:3736–3748

Evans EF, Zhao W (1998) Periodicity coding of the fundamental frequency of harmonic complexes: physiological and pharmacological study of onset units in the ventral cochlear nucleus. In: Psychophysical and physiological advances in hearing. Proceedings of the 11th international symposium on hearing, 1997. Whurr, London

Knudsen VO (1929) The hearing of speech in auditoriums. J Acoust Soc Am 1:56–82

Louage DH, van der Heijden M, Joris PX (2004) Temporal properties of responses to broadband noise in the auditory nerve. J Neurophysiol 91:2051–2065

Merrill EG, Ainsworth A (1972) Glass-coated platinum tipped tungsten microelectrodes. Med Biol Eng 10:662–672

Nàbeˇlek AK, Letowski TR, Tucker FM (1989) Reverberant overlapand self-masking in consonant identification. J Acoust Soc Am 86:1259–1265

Santon F (1976) Numerical prediction of echograms and of the intelligibility of speech in rooms. J Acoust Soc Am 59:1399–1405

Shackleton TM, Carlyon RP (1994) The role of resolved and unresolved harmonics in pitch perception and frequency modulation discrimination. J Acoust Soc Am 95:3529–3540

Watkins AJ (2005) Perceptual compensation for effects of reverberation in speech identification. J Acoust Soc Am 118:249–262

Comment by Langner

Your results may be explained by the way pitch information is mapped in the inferior colliculus (IC). As we have shown by single unit recordings as well as by functional mapping with the 2-Deoxyglucose method, a harmonic sound is represented by a column of activated neurons parallel to the tonotopic gradient. The activation of low frequency neurons is due to resolved harmonics, possible distortion products, and across frequency activation in the IC. The activation of neurons with higher CFs requires periodicity coding (according to my model by a cross-correlation of envelope periodicity with resolved harmonics). If you cut the lowest harmonics from the stimulus, the neuronal column is still (partly) activated, because periodicity coding works for higher harmonics. If you destroy periodicity information by reverberation, the column is (partly) activated by resolved harmonics alone. In either case, pitch remains encoded in the same way, by the same neuronal column in the IC.

widths (see the legend) produce a strong excitatory response when the upper-frequency edge of the notch is near BF (vertical dashed line) and inhibition when the notch is centered on BF (when the upper edge frequency is just above BF). This pattern of response remains across a range of sound levels (Fig. 2B, for 1/2 octave notches). It is also observed when the stimulus is a noise band, but in this case is associated with the lower-frequency edge of the band, on the abscissa in Fig. 2C.

3Finding the Optimal Stimulus

A useful approach to understanding the sensory representation by nonlinear neurons is to search for optimal stimuli (e.g. deCharms et al. 1998; O’Connor et al. 2005). The characteristics of a neuron’s optimal stimulus provide a functional definition of the signal processing being done by the neuron. The optimum can be the stimulus giving the highest discharge rate or it can be the stimulus about which the neuron provides the most information in some sense. In this chapter the optimum is the maximum discharge rate.

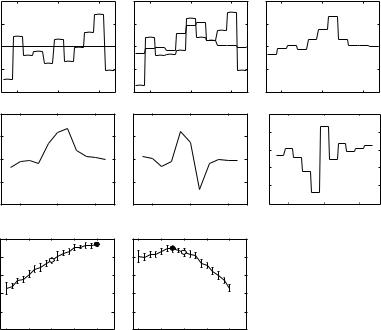
The problem of finding the optimum is not well defined and must usually be limited to some class of stimuli. Here, the stimulus class is random spectral shape stimuli (RSS; Yu and Young 2000; Young and Calhoun 2005) and the optimum spectral shape is sought. RSS stimuli consist of sums of random-phase tones spaced at 1/64 octave intervals over a several-octave frequency range; the tones are gathered into sets of 8 in 1/8 octave bins. The total power in each bin, in dB relative to a reference stimulus, varies pseudo-randomly with an approximately Gaussian distribution and a standard deviation of 1.5–12 dB. These stimuli have minimal envelope fluctuations and the effects of the temporal envelope are not considered. Figure 3A shows examples of the spectra of RSS stimuli.

The optimization proceeds by changing the spectral shape iteratively, guided by the Fisher information matrix F of the responses (Cover and Thomas 1991). The i–jth term in the Fisher matrix is

where p(r; q) is the pdf of discharge rate r given the stimulus parameters q, the amplitudes (dB) of the stimulus in the 11 RSS bins centered on BF. Fij is the sensitivity of the neuron’s rate response to simultaneous changes in the stimulus amplitude in the ith and jth bins, in the sense that the inverse of the Fisher matrix is the covariance matrix of the minimum-variance unbiased estimator of q based on r (the Cramér-Rao bound). The Fisher matrix can be computed from rate data using the following approximation (Johnson et al. 2001):