6.2. Основные элементы сетевого графика и правила его построения

Сетевая модель комплекса работ, подлежащих выполне­нию при сооружении конкретного объекта, в обязательном порядке содержит собственно сеть и может включать ряд ха­рактеристик (объем, время, стоимость, ресурсы и др.), отно­сящихся к отдельным работам и (или) к комплексу в целом.

Сеть с математической точки зрения представляет собой ориентированный, связный, конечный граф без контуров, от­ражающий реально существующие отношения предшество­вания между работами комплекса. В сетевой модели приме­няют ориентированные графы, т. е. фигуры, состоящие из вершин и дуг.

Примерами применения графов могут служить различ­ные карты, схемы, диаграммы и т. п. Вершинами в этих слу­чаях являются населенные пункты (в географических кар­тах), источники электроснабжения и потребители (в электри­ческих схемах), объемы ресурсов, количество рабочей силы (в графиках-диаграммах). Возможны и другие формы пред­ставления - цифровая, табличная, с помощью различных тех­нических средств (световое табло, механические модели и др.).

Наибольшее распространение получило графическое представление сетевой модели на плоскости, называемое се­тевым графиком, которое появилось в нашей стране еще в 1925 г. и было описано в книге А. А. Эрасмуса [66]. Сетевой график представляет собой сетевую модель с рассчитанными временными и ресурсными параметрами.

Широкое распространение сетевого моделирования в строительстве в форме сетевых графиков объясняется сле­дующими преимуществами:

• на сетевом графике легко выделять работы, от кото­рых зависит срок строительства, и обеспечивается нагляд­ность технологической последовательности работ;

• руководителю строительной организации дается воз­можность прогнозировать и контролировать ход строительст­ва, так как на графике детально определена взаимосвязь ме­жду работами;

• установлены основные и второстепенные работы, и поэтому руководитель может сосредоточить свое внимание на основных работах;

• выполненные расчеты по сетевому графику позволя­ют постоянно наблюдать за резервами времени, материально- техническими ресурсами и узкими местами;

• сетевым графиком охватываются обычно вопросы обеспечения строительства материально-техническими ре­сурсами и проектной документацией, что даст возможность установить зависимость строительства от этих факторов;

• нет необходимости пересоставления графика в случа­ях изменения конкретных условий производства работ на строительной площадке, достаточно изменить цифры, пока­зывающие продолжительность работ.

Для крупных объектов строительства с числом работ от 200 и более очень трудно пользоваться календарным планом, а при сетевых графиках сравнительно легко выполняются расчеты длины путей и резервы времени по специальным программам на электронно-вычислительных машинах, что резко повышает производительность труда ИТР, расчеты се­тевых графиков с небольшим набором работ легко и просто выполняются вручную.

Как показала практика, использование сетевых графи­ков наиболее целесообразно для промышленного, массового жилищного и культурно-бытового строительства. Для типо­вого жилищного строительства применение сетевых графи­ков нецелесообразно потому, что принадлежность и очеред­ность работ заранее известна и многократно проверена. По­этому здесь должны применяться в основном монтажно-транспортные графики, с помощью которых устанавливается взаимоувязанная работа транспорта и строительного произ­водства в соответствии с принятым планом.

Целями применения сетевых графиков являются разра­ботка оптимального или достаточно близкого к нему вариан­та плана строительства, обеспечивающего рациональную увязку во времени и пространстве выполняемых работ и наи­лучшее использование ресурсов, а также эффективное управ­ление процессом реализации этого плана. В результате при­менения сокращается продолжительность строительства, сни­жается его трудоемкость и себестоимость, растет производи­тельность труда.

Сетевой график позволяет установить перечень тех ра­бот, от которых непосредственно зависит продолжительность строительства, и осуществлять контроль за ходом их выпол­нения руководителями строительных организаций. Работы, не попавшие в этот перечень, являются определенным запа­сом во времени и ресурсах, что позволяет смещать их в неко­торых пределах по срокам и передавать предназначенные для них ресурсы на работы, лежащие на критическом пути.

В основе системы сетевого планирования и управления строительством лежит сетевая модель — графическое изо­бражение плана, которое получило в литературе название се­тевого графика. Сетевой график представляет собой схему, на которой наглядно показаны все работы по созданию сна­чала промежуточной продукции определенной степени го­товности, а под конец - полное возведение объекта строи­тельства.

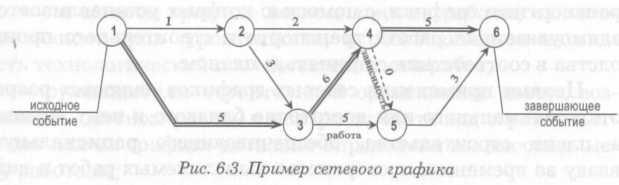
По внешнему виду сетевой график представляет собой сеть, состоящую из стрелок и кружков, отражающих логиче­скую и технологическую взаимосвязь и взаимообусловлен­ность всех операций, входящих в общий комплекс работ стро­ящегося объекта (рис. 6.3). В этом способе стрелками обозна­чают работы, а кружками с цифрами-индексами (кодами) - события. Образуемая из сочетания работ и событий сеть представляет собой весь процесс создания объекта.

Для построения сети используются такие элементы сете­вого графика, как работа, зависимость, событие, продолжи­тельность и путь.

Работа, обозначаемая в сетевом графике стрелкой, мо­жет выражать:

• действительную работу, т. е. производственный про­цесс, требующий затрат труда, времени и ресурсов (напри­мер, отрывка котлована, монтаж фундаментов и т. д.). На се­тевых графиках работу принято изображать сплошной стрел­кой с надписью над ней названия или шифра работы, а под ней - продолжительности выполнения работы;

• ожидание, которое представляет собой тоже работу, но требующую только затрат времени и не требующую затрат каких-либо ресурсов. Как правило, к ожиданиям относятся тех­нологические и организационные перерывы. Ожидание, как и действительная работа, обозначается сплошной стрелкой;

• зависимость или фиктивная работа отражает техно­логическую или организационную взаимосвязь работ и не требует ни времени, ни ресурсов. В сетевом графике зависи­мость обозначается пунктирной стрелкой (см. рис. 6.3), ука­зывающей что выполнение последующих за ней работ воз­можно только при условии предварительного выполнения предшествующих работ.

Факт окончания одной или нескольких работ, необхо­димых и достаточных для начала следующих работ, назы­вают событием. Всякая работа сетевого графика ограниче­на двумя событиями. Подразумевается, что событие совер­шается мгновенно, и поэтому оно не требует ни времени, ни ресурсов. Событие на сетевом графике обычно изображает­ся кружком. Внутри кружка указывают код события, кото­рый только определяет события, но не указывает их после­довательность.

В сетевой график всегда входят особые события: исход­ное и завершающее. Исходное событие не имеет предшест­вующих работ. Этим событием начинается развитие сетевого графика. Завершающее событие не имеет последующих работ и завершает работы в сетевом графике.

Каждая работа в сетевом графике имеет свою продолжи­тельность, которая на сетевом графике указывается над стрелкой. Пройдя от исходного события к завершающему, по­следовательно по цепочке зависимостей можно подсчитать общую продолжительность всех работ.

Взаимосвязанные между собой работы и события обра­зуют пути сетевого графика. Путем называется такая после­довательность работ в сети, у которой конечное событие каж­дой работы совпадает с начальным событием следующей за ней работы.

В сетевом графике различают несколько видов путей. Путь от исходного до завершающего события сетевого гра­фика называют полным путем.

Самый длинный из всех полных путей (их может быть не­сколько) имеет особое значение - его временная длина опреде­ляет срок выполнения работ по сетевому графику, поэтому на графике он выделяется двойной или жирной линией и называ­ется критическим путем. В сетевом графике может быть не­сколько критических путей. Работы, которые лежат на крити­ческом пути, называют критическими. Путь, длина которого несколько меньше критического, называют подкритическим.

Совокупность критических и подкритических путей об­разует критическую зону.

Выявление в сетевом графике критической зоны позво­ляет выявить работы, на которые нужно обращать внимание при необходимости сокращения сроков строительства при проектировании сетевого графика или при контроле за ходом строительства.

Каждая работа и ее результат должны иметь четкое определение. Последовательность выполнения работ устанавливается в соответствии с требованиями технологии строительства объекта. При этом осуществляют работы, вы­полняемые последовательно, т. е. начало следующей работы после окончания предшествующей, и работы, выполняемые параллельно. Схематическое изображение этой последова­тельности и взаимосвязей работ на графике называют топо­логией сетевой модели.

Сетевой моделью необходимо отразить правильную за­висимость работ, соответствующую принятым методам орга­низации и производства работ. Для этого надо соблюдать следующие правила построения сетевого графика:

• все стрелки (работы) должны быть направлены слева направо в сторону развивающегося графика к конечному со­бытию¹; длины и углы наклона стрелок, символизирующих работы, выбираются произвольно (длина стрелки не отража­ет в масштабе продолжительность работы);

• все вершины сетевого графика (события) должны быть пронумерованы;

• нумерация событий производится последовательно от исходного к завершающему;

• пересечение стрелок допустимо, но нежелательно;

• в сетевой модели не должно быть «тупиковых» собы­тий, т. е. событий, из которых не выходит ни одна работа, за исключением завершающего события. Здесь либо работа не нужна и ее следует аннулировать, либо не замечена необхо­димость определенной работы, следующей за событием для свершения какого-либо последующего события. В таких слу­чаях необходимо тщательное изучение взаимосвязей событий и работ для исправления возникшей ошибки;

• в сетевой модели не должно быть «хвостовых» собы­тий (кроме исходного), которым не предшествует хотя бы одна работа. Обнаружив в сети такие события, необходимо определить исполнителей предшествующих им работ и вклю­чить эти работы в сеть;

• в сети не должно быть замкнутых контуров (циклов) и петель, т. е. путей, соединяющих некоторые события с ними же самими. При возникновении контура необходимо вернуть­ся к исходным данным и путем пересмотра состава работ до­биться его устранения;

• любые два события должны быть непосредственно связаны не более чем одной работой-стрелкой. Нарушение этого условия происходит при изображении параллельно вы­полняемых работ. Если эти работы оставить, то произойдет путаница из-за того, что две различные работы будут иметь одно и то же обозначение. Однако содержание этих работ, со­став привлекаемых исполнителей и количество затрачивае­мых на работы ресурсов могут существенно отличаться. В этом случае рекомендуется ввести фиктивное событие и фиктивную работу, при этом одна из параллельных работ за­мыкается на это фиктивное событие;

• в сети рекомендуется иметь одно исходное и одно за­вершающее событие. Если в составленной сети это правило нарушено, то исправить ошибку можно путем введения фик­тивных событий и работ.

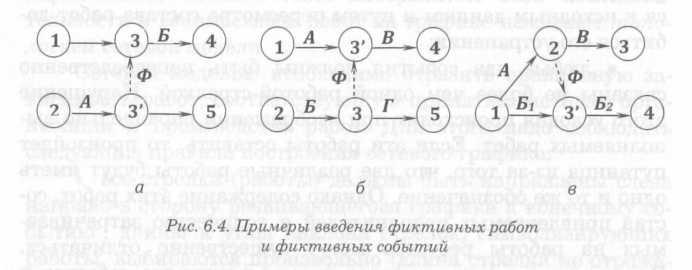
Фиктивные работы и события необходимо вводить и в ря­де других случаев. Один из них - отражение зависимости со­бытий, не связанных с реальными работами. Например, рабо­ты А и Б (рис. 6.4, а) могут выполняться независимо друг от друга, но по условиям производства работа Б не может начать­ся раньше, чем окончится работа А. Это обстоятельство требует введения фиктивной работы Ф и фиктивного события 3’.

Другой случай - неполная зависимость работ. Например, работа В требует для своего начала завершения работ А и Б, а работа Г связана только с работой Б и от работы А не зави­сит. Тогда требуется введение фиктивной работы Ф и фик­тивного события 3’, как показано на рис. 6.4, б.

Кроме того, если последующая работа зависит от части предшествующей, то последнюю следует изобразить двумя стрелками, вводя между ними промежуточное (дополнитель­ной) событие. Например, работа В (рис. 6.4, в) может начать­ся после полного окончания работы А и частичного оконча­ния работы Б. Это требует введения между частями работы Б фиктивного события 3’.

-

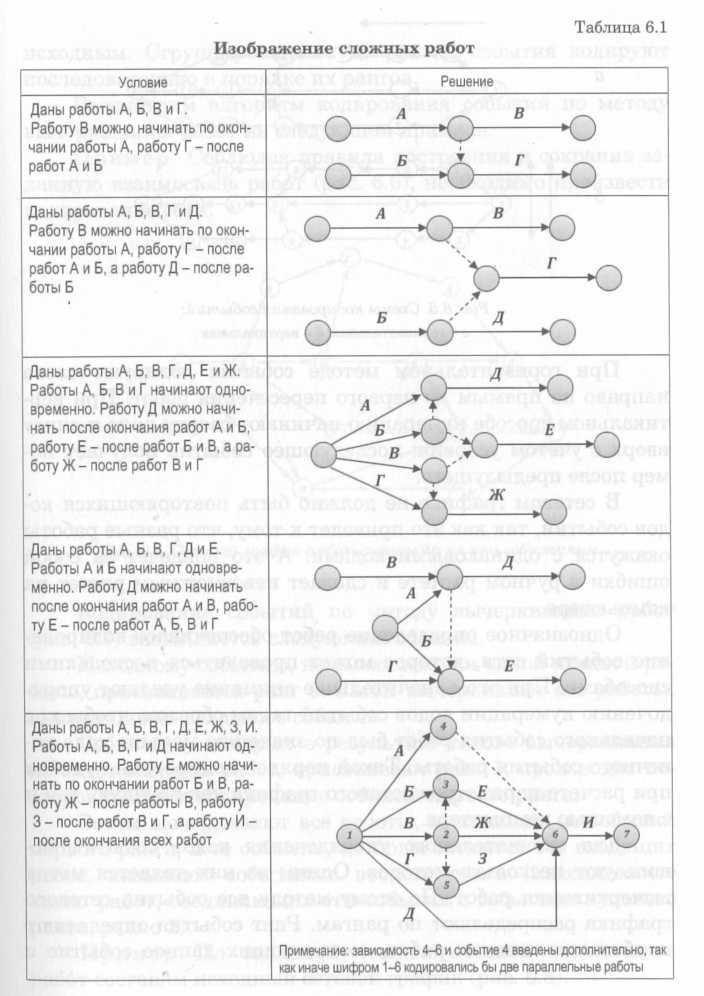
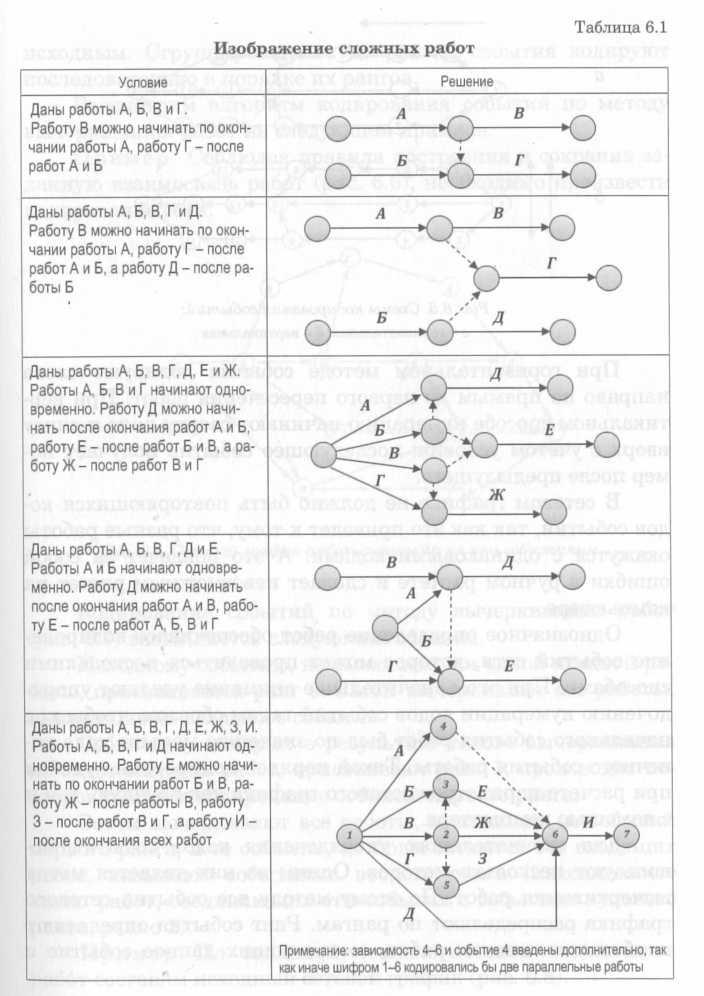
Также фиктивные работы могут вводиться для отра­жения реальных отсрочек и ожидания. В отличие от преды­дущих случаев здесь фиктивная работа характеризуется про­тяженностью во времени. В табл. 6.1 приведено схематиче­ское изображение последовательности и взаимосвязей слож­ных работ на сетевом графике.

Таблица 6.1. – Изображение сложных работ

Условие	Решение
Даны работы А, Б, В и Г. Работу В можно начинать по окончании работы А, работу Г – после работ А и Б
Даны работы А, Б, В, Г и Д. Работу В можно начинать по окончании работы А, работу Г – после работ А и Б, а работу Д – после работы Б
Даны работы А, Б, В, Г, Д, Е и Жс. Работу В можно начинать по окончании работы А, работу Г – после работ А и Б, а работу Д – после работы Б

По окончании построения сетевого графика делается еще раз его проверка на предмет соблюдения в нем правиль­ной технологической последовательности выполнения работ согласно заданным условиям и устранения излишних пунк­тирных связей.

Затем выполняется нумерация событий, которая должна соответствовать последовательности работ во времени. Ис­ходному событию присваивается нулевой или первый номер. Последующее событие нельзя нумеровать, если не пронуме­ровано предшествующее ему событие.

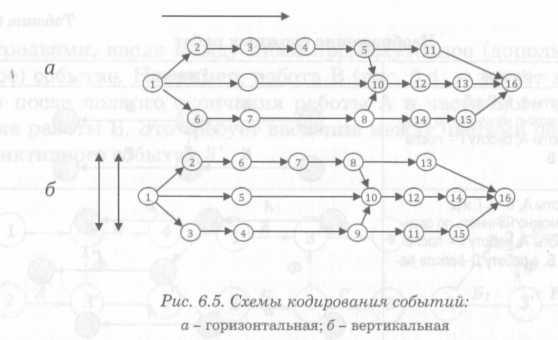
Кодирование (нумерация) событий сети обеспечивает од­нозначное определение работ и может проводиться несколь­кими способами. К упрощенным способам кодирования отно­сятся горизонтальный или вертикальный методы (рис. 6.5).

При горизонтальном методе события кодируют слева направо по прямым до первого пересечения работ. При вер­тикальном способе нумерацию начинают сверху вниз и снизу вверх с учетом условия: последующее событие получает но­мер после предыдущего.

В сетевом графике не должно быть повторяющихся ко­дов событий, так как это приведет к тому, что разные работы окажутся с одинаковыми кодами. А это повлечет за собой ошибки в ручном расчете и сделает невозможным расчет на компьютере.

Однозначное определение работ обеспечивает кодирова­ние событий сети, которое может проводиться несколькими способами. При этом значительное внимание уделяют упоря­дочению нумерации кодов событий таким образом, чтобы код начального события работ был по значению меньше кода ко­нечного события работы. Такой порядок кодирования удобен при расчете параметров сетевого графика как вручную, так и с помощью компьютера.

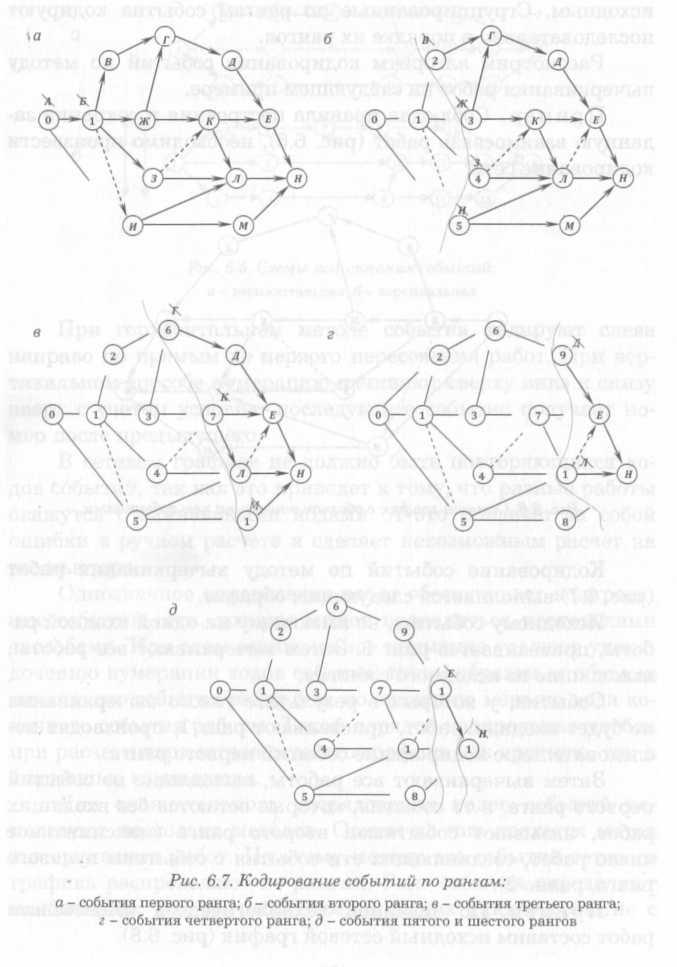
Для окончательного упорядочения кодов событий ис­пользуют несколько методов. Одним из них является метод вычеркивания работ. По этому методу все события сетевого графика распределяют по рангам. Ранг события определяют наибольшим числом работ, соединяющих данное событие с исходным. Сгруппированные по рангам события кодируют последовательно в порядке их рангов.

Рассмотрим алгоритм кодирования событий по методу вычеркивания работ на следующем примере.

Пример. Соблюдая правила построения и сохранив за­данную взаимосвязь работ (рис. 6.6), необходимо произвести кодирование сети.

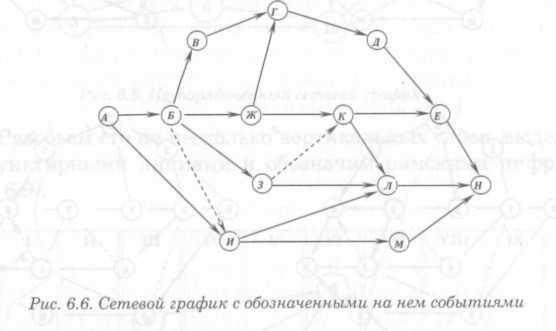
Кодирование событий по методу вычеркивания работ (рис. 6.7) выполняется следующим образом.

Исходному событию, не имеющему ни одной входной ра­боты, присваивается ранг 0. Затем вычеркивают все работы, выходящие из исходного события.

События, у которых в результате такого вычеркивания не будет входных работ, присваивают ранг 1, производят по­следовательное кодирование событий первого ранга.

Затем вычеркивают все работы, выходящие из событий первого ранга, и те события, которые остаются без входящих работ, называют событиями второго ранга (максимальное число работ, соединяющих эти события с событием нулевого ранга, равно 2).

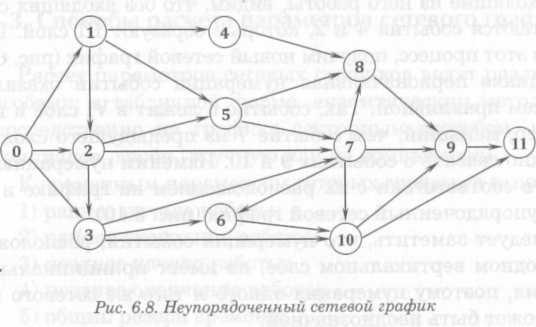
Пример. По заданной технологической взаимосвязи работ составим исходный сетевой график (рис. 6.8).

Разобьем его на несколько вертикальных слоев, выделим их пунктирными линиями и обозначим римскими цифрами (рис. 6.9).

Поместив в I слой начальное событие 0, мысленно вы­черкнем из графика это событие и все выходящие из него работы-стрелки. Тогда без входящих стрелок останется собы­тие 1, образующее II слой. Вычеркнув мысленно событие 1 и все выходящие из него работы, видим, что без входящих стре­лок остаются события 4 и 2, которые образуют III слой. Про­должая этот процесс, получим новый сетевой график (рис. 6.9).

Однако первоначальная нумерация событий оказалась не совсем правильной. Так, событие 6 лежит в VI слое и име­ет номер, меньший, чем событие 7 из предыдущего слоя. То же можно сказать о событиях 9 и 10. Изменим нумерацию со­бытий в соответствии с их расположением на графике и по­лучим упорядоченный сетевой график (рис. 6.10).

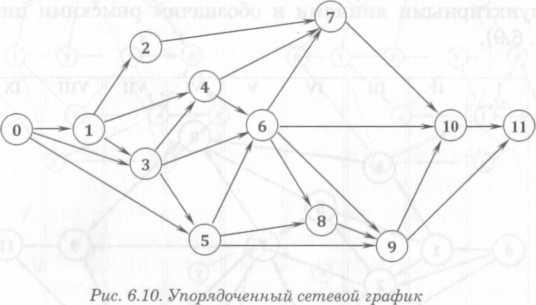
Следует заметить, что нумерация событий, расположен­ных в одном вертикальном слое, не имеет принципиального значения, поэтому нумерация одного и того же сетевого гра­фика может быть неоднозначной.

Поскольку работы могут быть логически связаны друг с другом, то необходимо всегда перед построением сетевого графика дать ответы на следующие вопросы:

• какие работы необходимо завершить непосредственно перед началом рассматриваемой работы;

• какие работы должны непосредственно следовать по­сле завершения данной работы;

• какие операции могут выполняться одновременно с рассматриваемой работой?