ностей принципиального порядка.

Особенно любопытно движение на эллиптическом столе с фокусами F1 и F2. Так как касательная к эллипсу образует одинаковые углы с отрезками, проведенными из фокусов в точку касания, то каждая траектория, проходящая через один из фокусов, дает отражение, проходящее через другой фокус, и т. д. Нетрудно усмотреть, что после n отражений, независимо от начального положения, траектория при n, неограниченно возрастающем, будет приближаться к большой оси F1F2. Если начальный луч не проходит через фокус, то возникают две возможности. Или начальный луч проходит между фокусами: тогда все отраженные траектории будут проходить между фокусами, причем будут касательными к некоторой гиперболе с теми же фокусами F1 и F2. Или же начальный луч не разделяет фокусов: тогда этим же свойством будут обладать все отраженные лучи, причем все они будут касаться некоторого эллипса с теми же фокусами F1 и F2. Таким образом, движение внутри эллипса ни при каких начальных условиях не оказывается эргодическим.

Упражнения. 1) Докажите, что если начальный луч проходит через какой-нибудь фокус эллипса, то его n-е отражение при неограниченном возрастании n стремится к большой оси.

2) Докажите, что если начальный луч проходит между фокусами эллипса, то этим же свойством обладают все отраженные лучи, и все они касательны к некоторой гиперболе с фокусами F1 и F2; точно так же, если начальный луч не проходит между фокусами, то этим же свойством обладают все отраженные лучи, и все они касательны к некоторому эллипсу с фокусами F1 и F2. (Указание: установите, что до отражения и после отражения в точке R луч образует соответственно одинаковые углы с отрезками RF1 и RF2, потом докажите, что софокусные конические сечения характеризуются отмеченным обстоятельством.)

§5. Проблема Штейнера

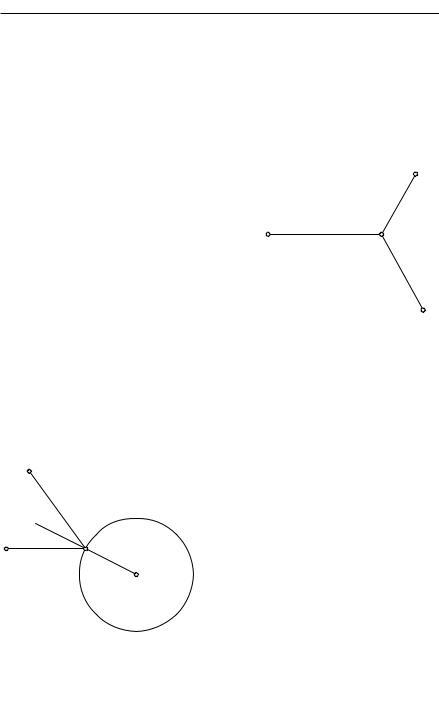
1.Проблема и ее решение. Очень простая и вместе с тем поучительная проблема была изучена в начале прошлого столетия знаменитым берлинским геометром Якобом Штейнером. Требуется соединить три деревни A, B, C системой дорог таким образом, чтобы их общая протяженность была минимальной. В более точной математической формулировке: на плоскости даны три точки A, B, C; требуется найти такую четвертую точку P , чтобы сумма a + b + c (где a, b, c — расстояния P соответственно от A, B, C) обратилась в минимум. Решение проблемы таково: если в треугольнике ABC все углы меньше 120◦, то в качестве точки P следует взять ту, из которой все три стороны AB, BC, CA видны под углом в 120◦; если же один из углов треугольника ABC, например C, больше или равен 120◦, то точку P нужно совместить с вершиной C.

384 МАКСИМУМЫ И МИНИМУМЫ гл. VII

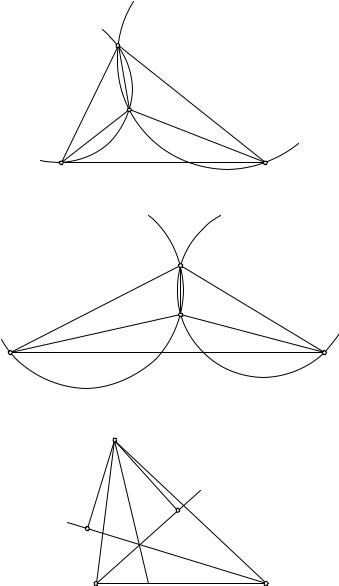
2. Анализ возникающих возможностей. Чтобы установить, которая именно из двух возможностей имеет место, нам придется обратиться к построению точки P . Для нахождения точки P , из которой две стороны треугольника, например AC и BC, видны под углом в 120◦, достаточно через точки A, C провести такую окружность K1, у которой меньшая из дуг AC содержала бы 120◦, и через точки B, C провести окружность K2, обладающую таким же свойством; затем взять точку пересечения двух дуг, содержащих по 120◦, если только эти дуги действительно пересекаются. Из точки P , найденной таким образом, сторона AB непременно также будет видна под углом в 120◦, так как сумма трех углов с вершиной P равна 360◦.

Из рис. 210 видно, что если все три угла треугольника ABC меньше 120◦, то две упомянутые дуги непременно пересекутся внутри треугольника. С другой стороны, если один из углов треугольника ABC, например C, больше чем 120◦, то дуги, о которых идет речь, не пересекутся (рис. 211). В этом случае не существует точки P , из которой каждая из трех сторон ABC была бы видна под углом в 120◦: окружности K1 и K2 пересекаются в точке P 0, из которой стороны AC и BC видны под углом в 60◦, и только одна сторона AB, противолежащая тупому углу, видна под углом в 120◦.

Если один из углов треугольника больше 120◦, то, как мы только что видели, нет такой точки P , из которой каждая из сторон видна под углом в 120◦; значит, искомая точка (в которой достигается минимум) должна совпадать с одной из вершин (так как это на основании § 1 — единственная иная возможность), а именно, с вершиной тупого угла.

Если же у треугольника все углы меньше 120◦, тогда, как мы видели, точку P , из которой все стороны видны под углом в 120◦, можно построить. Но, чтобы доказательство было закончено, нужно еще доказать, что для такой точки P сумма a + b + c меньше, чем для любой из вершин треугольника (так как еще покамест неизвестно, которая из двух возможностей в рассматриваемом случае имеет место). Итак, докажем, например, что a + b + c меньше, чем AB + AC (рис. 212). С этой целью продолжим отрезок BP и спроектируем точку A на полученную прямую; пусть найденная проекция есть D. Так как, очевидно, AP D = 60◦, то длина проекции P D равна 12 a. Так как BD есть проекция AB на пря-

мую BP , то, значит, BD < AB. Но BD = b + 12 a; поэтому b + 12 a < AB. Совершенно таким же образом, проектируя A на продолжение отрез-

ка P C, мы убеждаемся, что c + 12 a < AC. Складывая два последних

неравенства, получаем: a + b + c < AB + AC. Итак, искомая точка не может находиться в вершине A. Так как, аналогично, она не может

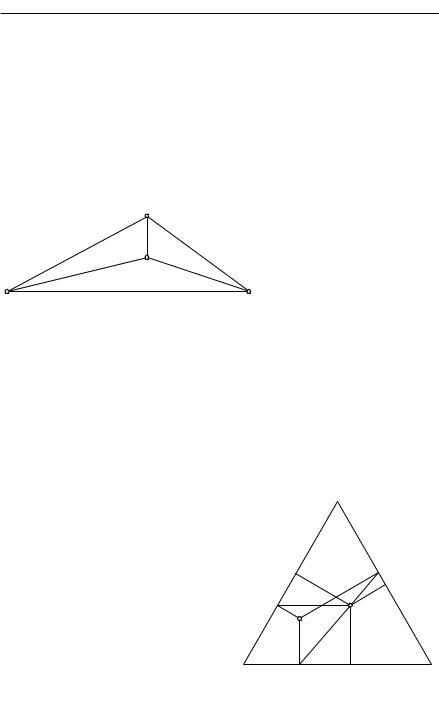
4. Замечания и упражнения. Из произвольной точки P , взятой внутри равностороннего треугольника UV W , опустим перпендикуляры P A, P B, P C на три стороны (рис. 214). Тогда точки A, B, C и P образуют как раз такую фигуру, как мы рассматривали выше. Это замечание может быть использовано при решении проблемы Штейнера: достаточно, исходя из точек A, B, C, найти вершины равностороннего треугольника U, V , W .

Упражнения. 1) Выполните указанное построение, основываясь на том обстоятельстве, что сумма трех перпендикуляров, опущенных на стороны из произвольной точки P внутри равностороннего треугольника, постоянна, а именно, равна высоте треугольника.

2) Основываясь на аналогичном обстоятельстве в случае, когда P находится вне UV W , исследуйте дополнительную проблему.

В трехмерном пространстве можно рассмотреть проблему, подобную штейнеровской: по заданным четырем точкам A, B, C, D найти такую пятую точку P , чтобы сумма a + b + c + d обращалась в минимум.

* Упражнение. Исследуйте эту трехмерную проблему и дополнительную к ней методами § 1 или же пользуясь правильным тетраэдром.

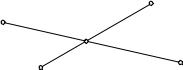
5. Обобщение: проблема уличной сети. В проблеме Штейнера были заданы три точки A, B, C. Было бы естественно обобщить эту проблему на случай n заданных точек A1, A2, . . . , An следующим образом: требуется найти в плоскости такую точку P , чтобы сумма расстояний a1 + a2 + . . . + an (где ai обозначает расстояние P Ai) обращалась в минимум. (В случае четырех точек, расположенных так, как показано

верхностным обобщением, подобных которому немало встречается в математической литературе. Чтобы по-

лучить действительно достойное внимания обобщение проблемы Штейнера, приходится отказаться от поисков одной-единственной точки P . Вместо того поставим задачей построить «уличную сеть» или «сеть дорог между данными деревнями», обладающую минимальной общей длиной. Точнее, даны n точек A1, A2, . . . , An; требуется найти такую связную систему прямолинейных отрезков, чтобы: 1) любые две из данных точек могли быть связаны ломаной линией, стороны которой входили бы в состав системы, 2) общая длина всей системы была наи-