
- •К русскому читателю
- •Как пользоваться книгой
- •Что такое математика?
- •Натуральные числа
- •Введение
- •Операции над целыми числами
- •Бесконечность системы натуральных чисел. Математическая индукция
- •Введение
- •Математическая числовая система
- •Введение
- •Рациональные числа
- •Несоизмеримые отрезки. Иррациональные числа, пределы
- •Рациональные числа и периодические десятичные дроби.
- •Замечания из области аналитической геометрии
- •Математический анализ бесконечного
- •Комплексные числа
- •Алгебраические и трансцендентные числа
- •Геометрические построения. Алгебра числовых полей
- •Введение
- •Основные геометрические построения
- •Неразрешимость трех классических проблем
- •Геометрические преобразования. Инверсия
- •Построения с помощью других инструментов. Построения Маскерони с помощью одного циркуля
- •Еще об инверсии и ее применениях
- •Проективная геометрия. Аксиоматика. Неевклидовы геометрии
- •Введение
- •Основные понятия
- •Двойное отношение
- •Параллельность и бесконечность
- •Применения
- •Аналитическое представление
- •Конические сечения и квадрики
- •Аксиоматика и нееклидова геометрия
- •Топология
- •Введение
- •Формула Эйлера для многогранников
- •Топологические свойства фигур
- •Другие примеры топологических теорем
- •Топологическая классификация поверхностей
- •Приложение
- •Функции и пределы
- •Введение
- •Независимое переменное и функция
- •Пределы
- •Пределы при непрерывном приближении
- •Точное определение непрерывности
- •Две основные теоремы о непрерывных функциях
- •Теорема Вейерштрасса об экстремальных значениях.
- •Некоторые применения теоремы Больцано
- •Максимумы и минимумы
- •Введение
- •Задачи из области элементарной геометрии
- •Общий принцип, которому подчинены экстремальные задачи
- •Стационарные точки и дифференциальное исчисление
- •Треугольник Шварца
- •Проблема Штейнера
- •Экстремумы и неравенства
- •Существование экстремума. Принцип Дирихле
- •Экстремальные проблемы элементарного содержания.
- •Изопериметрическая проблема
- •Вариационное исчисление
- •Вариационное исчисление. Принцип Ферма в оптике.
- •Экспериментальные решения задач на минимум. Опыты с мыльными пленками
- •Математический анализ
- •Введение
- •Интеграл
- •Примеры интегрирования. Интегрирование функции xr.
- •Производная
- •Техника дифференцирования
- •Обозначения Лейбница и «бесконечно малые»
- •Основная теорема анализа
- •Определение и свойства логарифма. Эйлерово число e.
- •Дифференциальные уравнения
- •Дифференциальное уравнение экспоненциальной функции. Радиоактивный распад. Закон роста. Сложные проценты.
- •Дополнительные замечания. Задачи и упражнения
- •Арифметика и алгебра
- •Аналитическая геометрия
- •Геометрические построения
- •Проективная и неевклидова геометрия
- •Топология
- •Функции, пределы, непрерывность
- •Максимумы и минимумы
- •Дифференциальное и интегральное исчисления
- •Техника интегрирования
- •О создании книги «Что такое математика?»
- •Рекомендуемая литература
- •Предметный указатель

§ 5 |
КОМПЛЕКСНЫЕ ЧИСЛА |
117 |
§5. Комплексные числа
1.Возникновение комплексных чисел. По ряду причин возникла потребность в расширении понятия числа даже за пределы континуума действительных чисел — посредством введения так называемых комплексных чисел. Необходимо ясно представлять себе, что все подобного рода расширения и нововведения приходят отнюдь не в результате чьих-то индивидуальных усилий. Скорее их можно рассматривать как итог некоторой постепенной и исполненной колебаний эволюции, в которой не следует преувеличивать роль отдельных личностей. Одной из причин, которые обусловили появление и употребление отрицательных
идробных чисел, было стремление к большей свободе в формальных вычислениях. Только к концу средневековья математики стали терять ощущение беспокойства и неуверенности, с которым они оперировали этими понятиями, тогда как ничего подобного не наблюдалось в отношении таких интуитивно ясных и конкретно воспринимаемых понятий, как понятие натурального числа.
Простейшая процедура, требующая применения комплексных чисел, есть решение квадратных уравнений. Напомним, как обстояло дело с линейным уравнением ax = b, когда нужно было определить удовлетворя-
ющее ему значение неизвестной величины x. Решение имеет вид x = ab ,
и введение дробных чисел как раз обусловливается требованием, чтобы всякое линейное уравнение с целыми коэффициентами (при a 6= 0) было разрешимо. Уравнения вроде
x2 = 2 |
(1) |
не имеют решения в области рациональных чисел, но имеют таковое в расширенном поле всех действительных чисел. Но даже поле действительных чисел недостаточно обширно, чтобы в нем можно было построить полную и законченную теорию квадратных уравнений. Например, следующее очень простое уравнение
x2 = −1 |
(2) |
не имеет действительных решений, так как квадрат действительного числа никак не может быть отрицательным. Нам приходится или удовольствоваться тем положением, что такие простые уравнения неразрешимы, или следовать по уже знакомому пути — расширять числовую область и вводить новые числа, с помощью которых удастся решить уравнение. Именно это самое и делается, когда вводят новый символ i и принимают, в качестве определения, что i2 = −1. Разумеется, этот объект — «мнимая единица» — не имеет ничего общего с числом как орудием счета. Это — отвлеченный символ, подчиненный основному закону i2 = −1, и ценность его зависит исключительно от того, будет ли достигнуто

118 |
МАТЕМАТИЧЕСКАЯ ЧИСЛОВАЯ СИСТЕМА |
гл. II |
в результате его введения действительно полезное расширение числовой системы.
Так как мы хотим складывать и умножать с помощью символа i так же, как с обыкновенными числами, то естественно пользоваться символами вроде 2i, 3i, −i, 2 + 5i, вообще, a + bi, где a и b — действительные числа. Раз эти символы должны подчиняться коммутативному, ассоциативному и дистрибутивному законам, то должны быть возможны, например, такие вычисления:
(2 + 3i) + (1 + 4i) = (2 + 1) + (3 + 4)i = 3 + 7i;
(2 + 3i) · (1 + 4i) = 2 + 8i + 3i + 12i2 = (2 − 12) + (8 + 3)i = −10 + 11i.
Руководствуясь этими соображениями, мы начинаем систематическое изложение теории комплексных чисел со следующего определения: символ вида a + bi, где a и b — два действительных числа, носит название
комплексного числа с действительной частью a и мнимой частью b. Операции сложения и умножения совершаются над этими числами так, как будто бы i было обыкновенное действительное число, однако с условием заменять i2 на −1. Точнее говоря, сложение и умножение определяются по формулам
) |
|
|
(a + bi) + (c + di) = (a + c) + (b + d)i, |
(3) |
|
(a + bi)(c + di) = (ac − bd) + (ad + bc)i. |
||
|
||
В частности, мы получаем |
|
|
(a + bi)(a − bi) = a2 − abi + abi − b2i2 = a2 + b2. |
(4) |
Основываясь на этих определениях, легко проверить, что для комплексных чисел справедливы коммутативный, ассоциативный и дистрибутивный законы. Далее, не только сложение и умножение, но также и вычитание и деление, будучи применены к двум комплексным числам, приводят снова к комплексным числам того же вида a + bi, так что комплексные числа образуют поле (см. стр. 75):
a + bi = |
(a + bi)(c − di) |
= |
|
ac + bd + |
|
bc − ad |
i. |
(5) |
||||
|
(a + bi) − (c + di) = (a − c) + (b |
− d)i, |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
c + di |
(c + di)(c − di) |
|
c2 + d2 |
c2 + d2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(Второе равенство теряет смысл, если c + di = 0 + 0i, так как тогда c2 + + d2 = 0. Значит, и на этот раз нужно исключить деление на нуль, т. е. на 0 + 0i.) Например,
(2 + 3i) − (1 + 4i) = 1 − i,
2 + 3i |
= |
2 + 3i |
· |
1 − 4i |
= |
2 − 8i + 3i + 12 |
= |
14 |
− |
5 |
|
i. |
||
|
|
|
|
|
|
|||||||||
1 + 4i |
1 + 4i |
17 |
17 |
|||||||||||
|
1 − 4i |
|
1 + 16 |
|
|
|||||||||
Поле комплексных чисел включает поле действительных чисел в качестве «подполя», так как комплексное число a + 0i отождествляется с

§ 5 |
КОМПЛЕКСНЫЕ ЧИСЛА |
119 |
действительным числом a. Заметим, с другой стороны, что комплексное число вида 0 + bi = bi называется «чисто мнимым».
Упражнения. |
1) Представьте |
(1 + i)(2 + i)(3 + i) |
в форме a + bi. |
||||||
|
|
(1 − i) |
|||||||
2) Представьте |
|
|
|
|
|
||||
− |
1 |
|
|
√ |
|
|
3 |
|
|
|
|
|
|
|
|||||
|
|
|
+ i |
3 |
|
|
|||
|
2 |
|
2 |
|
|
||||
вформе a + bi.
3)Представьте в форме a + bi следующие выражения:
|
1 + i |
, |
|
1 + i |
, |
|
1 |
, |
|
1 |
, |
(4 − 5i)2 |
. |
|||
|
1 − i |
|
|
2 − i |
|
i5 |
|
(−2 + i)(1 − 3i) |
|
|
(2 − 3i)2 |
|||||
|
√ |
|
|
|
|
|
|
|
|
√ |
|
|
||||
4) Вычислите |
|
5 + 12i |
. (Указание: напишите |
|
5 + 12i |
= x + yi, возведите |
||||||||||
в квадрат и приравняйте действительные части и мнимые части.)
Вводя символ i, мы расширили поле действительных чисел и получили поле символов a + bi, в котором квадратное уравнение
x2 = −1
имеет два решения: x = i и x = −i. В самом деле, согласно определению, i · i = (−i)(−i) = i2 = −1. Нужно сказать, что мы приобрели гораздо больше: можно легко проверить, что теперь каждое квадратное уравнение
ax2 + bx + c = 0 |
(6) |
становится разрешимым. В самом деле, выполняя над равенством (6) ряд преобразований, мы получаем:
|
|
x2 + |
b |
x = − |
c |
, |
|
|
|
|
|
|
||||||||||||||
|
a |
a |
|
|
|
|
|
|||||||||||||||||||
2 |
|
b |
|
|
|
|
|
|
b2 |
|
|
b2 |
|
|
c |
|
|
|||||||||
x + |
|
|
x + |
|
|
= |
|
− |
|
, |
|
|||||||||||||||
a |
4a2 |
4a2 |
a |
|||||||||||||||||||||||
|
x + |
|
b |
2 = b2 − 4ac |
, |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2a |
|
√ |
|
|
4a2 |
|
|
|
|
|
||||||||||||||
|
b |
|
|
b |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x + |
|
= |
|
± |
|
|
|
− 4ac |
, |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
2a |
|
|
|
|
|
2a |
|
|
|
|
|
|||||||||||
|
|
|
−b ± √ |
|
. |
|
|
|
|
|
||||||||||||||||
|
x = |
|
b2 − 4ac |
|
|
|
(7) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
|||
Заметим теперь, что если b2 − 4ac > 0, то √ |
|
есть обыкновен- |
||||||||||||||||||||||||
b2 − 4ac |
||||||||||||||||||||||||||
ное действительное число и корни уравнения (6) действительные; если |
||||||||||||
же b2 − 4ac < 0, то тогда 4ac − b2 > 0, и следовательно, √ |
|
= |
||||||||||
b2 − 4ac |
||||||||||||
= √ |
−(4ac − b2) |
= |
√ |
4ac − b2 |
· i, так что уравнение (6) имеет в качестве |
|||||||
корней мнимые числа. Так, например, уравнение |
|
|
|
|
||||||||
|
|
|
|
|
x2 − 5x − 6 = 0 |
|
|
|
|
|||
|
|
|
|
|
|
√ |
|
|
|
|
|
|
имеет действительные корни x = |
5 ± 25 − 24 |
= |
5 ± 1 |
= 3 или 2, тогда |
||||||||
как уравнение |
2 |
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
x2 − 2x + 2 = 0
120 |
|
МАТЕМАТИЧЕСКАЯ ЧИСЛОВАЯ СИСТЕМА |
|
|
|
|
|
гл. II |
||||||
|
|
|
|
√ |
|
|
|
|
1 |
|
i |
|
|
|
имеет мнимые корни |
x = 2 ± 4 − 8 = 2 ± 2i = 2 = 1 + i |
или |
− |
. |
|
|||||||||
|
2 |
2 |
|
|
|
|
||||||||
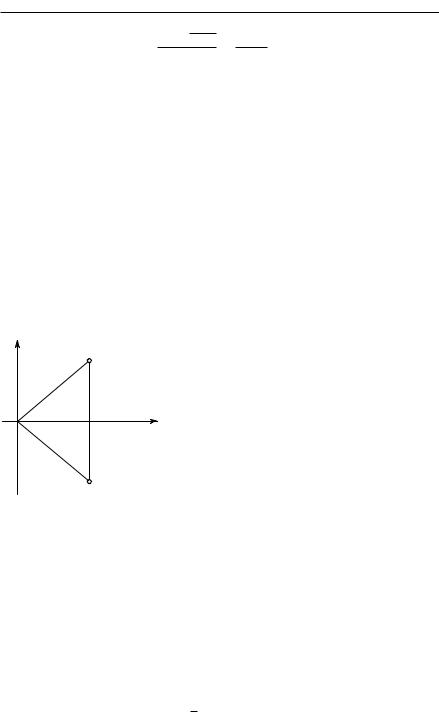
2. Геометрическое представление комплексных чисел. Уже |
||||||||||||||
в XVI столетии в математических работах появляются квадратные |
||||||||||||||
корни из отрицательных чисел в формулах, дающих решения квад- |
||||||||||||||
ратных уравнений. Но в те времена математики затруднились бы |
||||||||||||||
объяснить точный смысл этих выражений, к которым относились |
||||||||||||||
почти с суеверным трепетом. Сам термин «мнимый» до сих пор на- |
||||||||||||||
поминает нам о том, что эти выражения рассматривались как нечто |
||||||||||||||
искусственное, лишенное реального значения. И только в начале XIX в., |
||||||||||||||
когда уже выяснилась роль комплексных чисел в различных областях |
||||||||||||||
математики, было дано очень простое геометрическое истолкование |
||||||||||||||
комплексных чисел и операций с ними, и этим был положен конец |
||||||||||||||
сомнениям в возможности их законного употребления. Конечно, с совре- |
||||||||||||||
менной точки зрения, формальные операции с комплексными числами |
||||||||||||||
полностью оправдываются на основе формальных определений, так |
||||||||||||||
что геометрическое представление логически не является необходимым. |
||||||||||||||
Но такое представление, предложенное почти одновременно Весселем |
||||||||||||||
|
|
|
|
(1745–1818), Арганом (1768–1822) и Гаус- |
||||||||||
y |
|
|
|
сом, |
позволило рассматривать |
комплекс- |
||||||||
|
|
z |
|
ные числа и действия с ними как нечто |
||||||||||
|
|
|
|
вполне естественное с интуитивной точки |
||||||||||
|
|
|
|
зрения и, кроме того, имеющее чрезвычай- |
||||||||||
|
|
|
|
но большое значение в приложениях ком- |
||||||||||
O |
|
|
x |
плексных чисел как в самой математике, |
||||||||||
|
|
так и в математической физике. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Геометрическая |
интерпретация |
ком- |
||||||||
|
|
|
|
плексных чисел заключается в том, что |
||||||||||
|
|
|
|
комплексному числу z = x + yi |
сопостав- |
|||||||||
Рис. |
22. |
Геометрическое |
ляется точка на плоскости с координатами |
|||||||||||
x, y. Именно, действительная часть числа |
||||||||||||||
представление комплексных |
мыслится как x-координата, а мнимая — |
|||||||||||||
чисел. Точка z имеет прямо- |
||||||||||||||
как |
y-координата. |
Таким |
образом уста- |
|||||||||||
угольные координаты x, y |
||||||||||||||
навливается взаимно однозначное соответ- |
||||||||||||||
|
|
|
|
|||||||||||
ствие между комплексными числами и точками «числовой плоскости», |
||||||||||||||
подобно тому как нами было установлено раньше (см. § 2) соответствие |
||||||||||||||
между действительными числами и точками «числовой оси». Точкам |
||||||||||||||
на оси x в числовой плоскости соответствуют действительные числа |
||||||||||||||
z = x + 0 i, тогда как точкам на оси y — чисто мнимые числа z = 0 + yi. |
||||||||||||||
Если |
|
|
z = x + yi |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
есть какое-то комплексное число, то мы называем число
z = x − yi
§ 5 |
КОМПЛЕКСНЫЕ ЧИСЛА |
121 |
||
сопряженным с числом z. В числовой плоскости точка z получается из |
||||
точки z посредством зеркального отражения относительно оси x. Если |
||||
мы условимся расстояние точки z от начала обозначать через r, то на |
||||
основании теоремы Пифагора |
|
|
||
|
r2 = x2 + y2 = (x + yi)(x − yi) = z · z. |
|
||
Действительное число r = √x2 + y2 называется модулем z и обозначает- |
||||
ся |
r = |z|. |
|
|
|
|
|
|
||
Если z лежит на действительной оси, то модуль совпадает с абсолютной |
||||
величиной z. Комплексные числа с модулем 1 изображаются точками, |
||||
лежащими на «единичной окружности» с центром в начале и радиу- |
||||
сом 1. |
|
|
|
|
Если |z| = 0, то z = 0. Это следует из определения |z| как расстояния |
||||
точки z от начала. Далее, модуль произведения двух комплексных чисел |
||||
равен произведению модулей: |
|
|
||
|
|z1 · z2| = |z1| · |z2|. |
|
||
Это вытекает как следствие из более общей теоремы, которая будет |
||||
доказана на стр. 117. |
|
|
||
Упражнения. 1) Докажите последнюю теорему, исходя непосредственно |
||||
из определения умножения двух комплексных чисел z1 = x1 + y1i и z2 = x2 + |
||||
y2i. |
|
|
|
|
2) Пользуясь тем обстоятельством, что произведение двух действитель- |
||||
ных чисел равно нулю в том и только том случае, если один из множите- |
||||
лей равен нулю, докажите соответствующую теорему для комплексных чисел. |
||||
(Указание: основывайтесь при доказательстве на двух последних теоремах.) |
||||
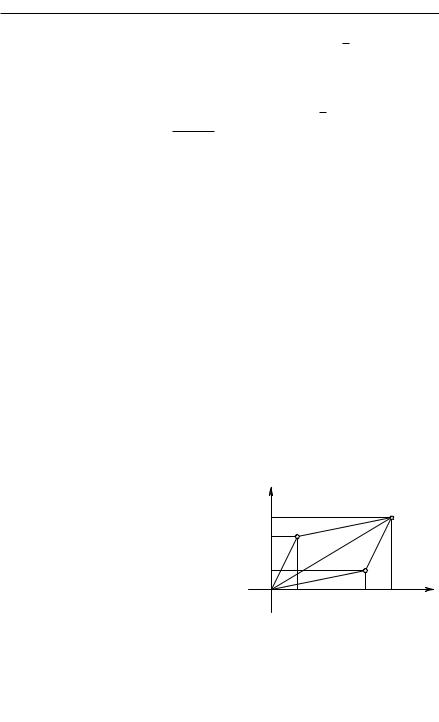
Согласно |
определению сложения |
|
|
|
двух комплексных чисел z1 = x1 + y1i |
y |
|
||
и z2 = x2 + y2i, мы имеем |
|
z1 |
||
z1 + z2 = (x1 + x2) + (y1 + y2)i. |
z2 |
|||
|
||||
Таким образом, точка z1 + z2 изоб- |
|
|
||
ражается в числовой плоскости чет- |
|
z1 |
||
вертой вершиной параллелограмма, у |
|
x |
||
которого тремя первыми вершинами |
O |
|||
являются точки 0, z1, z2. Это про- |
|
|
||
стой способ построения суммы двух |
Рис. 23. Сложение |
комплексных |
||
комплексных чисел ведет ко многим |
чисел по правилу параллелограм- |
|||
важным следствиям. Из него мы за- |
ма |
|
||
ключаем, что модуль суммы двух комплексных чисел не превышает |
||||
суммы модулей (ср. стр. 76): |
|
|
||
|
|z1 + z2| 6 |z1| + |z2|. |
|
||

122 |
МАТЕМАТИЧЕСКАЯ ЧИСЛОВАЯ СИСТЕМА |
гл. II |
Достаточно сослаться на то, что длина стороны треугольника не превышает суммы длин двух других сторон.
Упражнение. В каких случаях имеет место равенство |z1 + z2| = |z1| +
|z2|?
Угол между положительным направлением оси x и отрезком Oz называется аргументом z и обозначается буквой f (см. рис. 22). Числа z и z имеют один и тот же модуль
|z| = |z|,
но их аргументы противоположны по знаку:
f = −f.
Конечно, аргумент z определяется не однозначно, так как к нему можно прибавлять или из него вычитать любой угол, кратный 360◦, не изменяя направления отрезка Oz. Итак, углы
f, f + 360◦, |
f + 720◦, |
f + 1080◦, . . . |
f − 360◦, |
f − 720◦, |
f − 1080◦, . . . |
графически дают один и тот же аргумент. Так как, согласно определению синуса и косинуса,
x = r cos f, y = r sin f,
то любое комплексное число z выражается через его модуль и аргумент следующим образом:
|
z = x + yi = r(cos f + i sin f). |
(8) |
||||||||
Например, |
|
|
|
|
|
|
|
|
|
|
в случае |
z = i |
|
|
|
мы имеем |
r = 1, |
|
f = 90◦, |
||
» » |
z = 1 + i |
|
|
|
» |
» |
r = |
√ |
|
|
|
|
|
2, f = 45◦, |
|||||||
» » |
z = 1 − i |
|
|
|
» |
» |
r = |
√ |
|
|
√ |
|
|
2, f = −45◦, |
|||||||
» » |
z = −1 + |
3 |
i |
» |
» |
r = 2, |
|
f = 120◦, |
||
так что
i = 1 (cos 90◦ + i sin 90◦),
√
1 + i = 2 (cos 45◦ + i sin 45◦),
√
1 − i = 2 (cos(−45◦) + i sin(−45◦)),
√
−1 + 3 i = 2 (cos 120◦ + i sin 120◦).
Читатель может проверить эти утверждения посредством подстановки числовых значений тригонометрических функций.
Тригонометрическим представлением (8) очень полезно воспользоваться, чтобы уяснить себе геометрический смысл умножения двух комплексных чисел. Если
z = r(cos f + i sin f)
§ 5 |
|
КОМПЛЕКСНЫЕ ЧИСЛА |
123 |
||||
и |
|
z0 = r0(cos f0 |
+ i sin f0), |
|
|
||
|
|
|
|
||||
то |
|
|
|
|
|
|
|
zz0 = rr0 |
(cos f cos f0 − sin f sin f0) + (cos f sin f0 + sin f cos f0)i . |
||||||
Но, в силу |
основных теорем сложения синуса и косинуса, |
|
|||||
|
|
− sin f sin f0 |
|
|
|||
|
|
cos f cos f0 |
= cos(f + f0), |
|
|||
|
|
cos f sin f0 |
+ sin f cos f0 |
= sin(f + f0). |
|
||
Итак, |
|
zz0 = rr0{cos(f + f0) + i sin(f + f0)}. |
(9) |
||||
|
|
||||||
В правой части последнего равенства мы видим написанное в триго- |
|||||||
нометрической форме комплексное число с модулем rr0 и аргументом |
|||||||
f + f0. Значит, мы можем отсюда заключить, что при умножении двух |
|||||||
комплексных чисел их модули пере- |
|
|
|
|
|||
множаются, а аргументы склады- |
|
zz |
y |
|
|||
ваются (рис. 24). Таким образом, |
|
|
|
||||
|
|
|
|
||||
мы видим, что умножение комплекс- |
|
|
|
|
|||
ных чисел как-то связано с вращени- |
|
|
|
|
|||
ем. |
|
|
|
|
|
|
|
Установим точнее, в чем тут де- |
|
|
|
z |
|||
ло. Назовем направленный отрезок, |
|
|
z |
|
|||
идущий из начала в точку z, век- |
|
|
|
|
|||
тором точки z; тогда модуль r = |z| |
|
|
|
|
|||
есть его длина. Пусть z0 — какая- |
|
|
|
x |
|||
нибудь точка единичной окружно- |
|
|
O |
||||
сти, так что r0 = 1. В таком случае |
|
|
|
|
|||
умножение z на z0 просто повора- |
|
|
|
|
|||
чивает вектор z на угол f0. Если |
Рис. 24. |
Умножение |
комплексных |
||||
же r0 6= 1, то, помимо вращения, дли- |
чисел: аргументы складываются, |
||||||
на вектора должна быть умножена |
|
модули перемножаются |
|||||
на r0. Рекомендуем читателю само- |
|
|
|
|
|||
стоятельно проиллюстрировать эти факты, умножая различные ком- |
|||||||
плексные числа на z1 = i (вращение на 90◦); |
z2 = −i (тоже вращение |
||||||
на 90◦, но в обратном направлении); z3 = 1 + i и z4 = 1 − i. |
|
||||||
Формула (9) в особенности представляет интерес, если z = z0; в этом |
|||||||
случае имеем: |
|
|
|
|
|
||
|
|
z2 = r2(cos 2f + i sin 2f). |
|
||||
Умножая снова на z, будем иметь |
|
|
|
|
|||
z3 = r3(cos 3f + i sin 3f);
и, вообще, для любого n, повторяя операцию, получим
zn = rn(cos nf + i sin nf). |
(10) |

124 |
МАТЕМАТИЧЕСКАЯ ЧИСЛОВАЯ СИСТЕМА |
гл. II |
В частности, если точка z находится на единичной окружности, так что r = 1, мы приходим к формуле, открытой французским математиком А. де Муавром (1667–1754):
(cos f + i sin f)n = cos nf + i sin nf. |
(11) |
Эта формула — одно из самых замечательных и полезных соотношений в элементарной математике. Поясним это примером. Возьмем n = 3 и разложим левую часть по формуле бинома
(u + v)3 = u3 + 3u2v + 3uv2 + v3.
Тогда получим:
cos 3f + i sin 3f = cos3 3f − 3 cos f sin2 f + i(3 cos2 f sin f − sin3 f).
Одно такое комплексное равенство равносильно двум равенствам, связывающим действительные числа. В самом деле, если два комплексных числа равны, то в отдельности равны их действительные части и их мнимые части. Итак, можно написать
cos 3f = cos3 f − 3 cos f sin2 f, sin 3f = 3 cos2 f sin f − sin3 f.
Пользуясь затем соотношением
cos2 f + sin2 f = 1,
получим окончательно:
cos 3f = cos3 f − 3 cos f(1 − cos2 f) = 4 cos3 f − 3 cos f, sin 3f = −4 sin3 f + 3 sin f.
Подобного рода формулы, выражающие sin nf и cos nf соответственно через sin f и cos f, легко получить при каком угодно целом значении n.
Упражнения. 1) Напишите аналогичные формулы для sin 4f и cos 4f. 2) Предполагая, что точка z находится на единичном круге: z = cos f +
i sin f, покажите, что z1 = cos f − i sin f.
3)Без вычислений установите, что модуль числа aa +− bibi равен единице.
4)Докажите: если z1 и z2 — два комплексных числа, то аргумент z1 − z2 равен углу между положительным направлением действительной оси и вектором, идущим от z2 к z1.
5)Дан треугольник с вершинами z1, z2, z3; установите геометрический
смысл аргумента числа z1 − z2 . z1 − z3
6) Докажите, что отношение двух комплексных чисел с одинаковым аргу-
ментом есть действительное число. |
z3 − z1 |
|
z4 − z1 |
|
7) Докажите, что если аргументы чисел |
и |
равны между |
||
|
z3 − z2 |
|
z4 − z2 |
|
собой, то четыре точки z1, z2, z3, z4 лежат на окружности или на прямой линии, и обратно.
§ 5 |
|
|
|
|
|
КОМПЛЕКСНЫЕ ЧИСЛА |
|
|
|
125 |
|||
8) Докажите: четыре точки z1, z2, z3, z4 лежат на окружности или на |
|||||||||||||
прямой линии, если число |
z3 − z1 : z4 − z1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
действительное. |
|
|
|
z3 − z2 |
z4 − z2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
3. Формула Муавра и корни из единицы. Под корнем n-й сте- |
|||||||||||||
пени из числа a мы понимаем всякое такое число b, что bn = a. В частно- |
|||||||||||||
сти, |
число |
1 |
|
имеет |
два |
квадратных |
корня: |
1 |
и |
1, |
|||
как 1 |
2 |
= (−1) |
2 |
= 1. Число 1 име- |
|
|
|
|
− |
||||
так |
|
|
|
|
|
|
|
||||||
ет один действительный кубический ко- |
|
|
|
|
|
||||||||
рень, именно 1, тогда как оно же име- |
|
|
|
|
|
||||||||
ет четыре корня четвертой степени: два |
|
|
|
|
|
||||||||
действительных, 1 и −1, и два мнимых: i |
|
|
|
|
|
||||||||
и −i. Эти факты наводят на мысль, что в |
|
|
|
|
|
||||||||
комплексной области должно существо- |
|
|
|
|
1 |
||||||||
вать еще два кубических корня из 1 |
|
|
|
|
|
||||||||
(а всего кубических корней тогда будет |
|
|
|
|
|
||||||||
три). С помощью формулы Муавра мы |
|
|
|
|
|
||||||||
покажем, что эта догадка справедлива. |
|
|
|
|
|
||||||||
Мы убедимся, что в поле комплекс- |
|
|
|
|
|
||||||||
ных чисел существует ровно n корней |
Рис. |
25. Двенадцать |
|
корней |
|||||||||
степени n из 1. Эти корни изобража- |
двенадцатой степени из едини- |
||||||||||||
ются вершинами правильного n-уголь- |
|
цы |
|
|
|
||||||||
ника, вписанного в единичный круг и имеющего точку 1 в качестве |
|||||||||||||
одной из вершин. |
|
|
|
|
|
|
|
|
|
||||
Сказанное почти ясно из рис. 25 (соответствующего случаю n = 12). |
|||||||||||||
Первая вершина многоугольника есть 1. Следующая есть |
|
|
|
||||||||||
a = cos |
360◦ |
+ i sin |
360◦ |
, |
(12) |
|
n |
n |
|||||
|
|
|
|
так как аргумент должен равняться n-й части угла в 360◦. Еще следующая вершина есть a · a = a2, так как мы получим ее, вращая вектор a
на угол 360n ◦ . Дальше получаем вершину a3 и т. д.; после n шагов возвращаемся снова к вершине 1, т. е. получаем
an = 1,
что следует также из формулы (11), так как
cos 360n ◦ + i sin 360n ◦ = cos 360◦ + i sin 360◦ = 1 + 0 i = 1.
Итак, a1 = a есть корень уравнения xn = 1. То же справедливо относительно следующей вершины
a2 = cos 720n ◦ + i sin 720n ◦ .

126 |
МАТЕМАТИЧЕСКАЯ ЧИСЛОВАЯ СИСТЕМА |
гл. II |
Мы убедимся в этом, если напишем
(a2)n = a2n = (an)2 = 12 = 1,
или же воспользуемся формулой Муавра
(a2)n = cos n · 720n ◦ + i sin n · 720n ◦ = cos 720◦ + i sin 720◦ = 1 + 0 i = 1.
Точно так же мы заключаем, что все n чисел
1, a, a2, a3, . . . , an−1
являются корнями степени n из 1. Если будем степени увеличивать дальше или рассмотрим отрицательные степени, то новых корней не получим. В самом деле,
a−1 = 1 = an = an−1; a a
точно так же
an = 1, an+1 = (an) a = 1 · a = a,
и т. д., так что ранее полученные корни повторяются. Читателю предоставляем в качестве упражнения показать, что иных корней, кроме перечисленных, рассматриваемое уравнение не имеет.
Если n четное, то одна из вершин n-угольника попадает в точку −1, в соответствии с общеизвестным алгебраическим фактом: −1 есть корень четной степени из 1.
Уравнение, которому удовлетворяют корни n-й степени из 1,
xn − 1 = 0, |
(13) |
есть уравнение n-й степени, но легко понизить его степень на единицу. Воспользуемся алгебраической формулой
(xn − 1) = (x − 1)(xn−1 + xn−2 + xn−3 + . . . + 1). |
(14) |
Так как произведение двух чисел равно 0 в том и только том случае, если один из множителей равен нулю, то выражение (14) обращается в нуль или при x = 1, или при условии, что удовлетворяется уравнение
xn−1 + xn−2 + xn−3 + . . . + x + 1 = 0. |
(15) |
Этому уравнению удовлетворяют корни a, a2, . . . , an−1; оно называется
циклотомическим, или уравнением деления окружности. Так, например, мнимые кубические корни из 1
|
−1 + i |
√ |
|
|
a = cos 120◦ + i sin 120◦ = |
3 |
, |
||
|
2 |
√ |
|
|
a2 = cos 240◦ + i sin 240◦ = |
−1 − i |
3 |
||
|
|
|
||
|
2 |
|
|
|
являются корнями уравнения
x2 + x + 1 = 0,
§ 5 КОМПЛЕКСНЫЕ ЧИСЛА 127
как читатель сможет убедиться, выполняя подстановки. Таким же образом корни пятой степени из 1 (кроме самого числа 1) удовлетворяют
уравнению |
|
x4 + x3 + x2 + x + 1 = 0. |
(16) |
Чтобы построить правильный пятиугольник, нам приходится решить уравнение четвертой степени. Простое алгебраическое ухищрение — замена w = x + x1 — приводит к уравнению второй степени. Мы делим уравнение (16) на x2 и переставляем члены:
x2 + x12 + x + x1 + 1 = 0,
и, принимая во внимание, что x + x1 2 = x2 + x12 + 2, получаем w2 + w − 1 = 0.
По формуле (7) пункта 1 корни этого квадратного уравнения имеют вид
|
√ |
|
|
|
√ |
|
|
w1 = |
−1 + 5 |
, |
w2 = |
−1 − 5 |
. |
||
|
2 |
|
|
|
2 |
|
|
Итак, мнимые корни пятой степени из 1 являются корнями следующих двух квадратных уравнений:
x + |
1 |
= w1, |
или |
x2 + |
1 |
(√ |
|
− 1) x + 1 = 0, |
|
5 |
|||||||||
x |
2 |
||||||||
и |
|
|
|
|
(√ |
|
|
||
x + |
1 |
= w2, |
или |
x2 − |
1 |
5 |
+ 1) x + 1 = 0. |
||
x |
2 |
||||||||
Читатель сможет их решить по той же формуле (7).
Упражнения. 1) Найдите корни 6-й степени из 1.
2)Вычислите (1 + i)11.
3)Вычислите все различные значения выражений
√ |
|
|
√ |
|
|
|
√ |
|
|
√ |
|
|
|
|
1 + i, |
3 |
7 |
− 4i, |
3 |
i, |
5 |
−i. |
|||||
|
|
|
|
||||||||||
4) Вычислите 21i (i7 − i−7).
*4. Основная теорема алгебры. Не только уравнения вида ax2 + + bx + c = 0 или xn − 1 = 0 разрешимы в поле комплексных чисел, но можно утверждать гораздо больше: всякое алгебраическое уравнение степени n с действительными или комплексными коэффициентами
f(x) = xn + an−1xn−1 + an−2xn−2 + . . . + a1x + a0 = 0 |
(17) |
разрешимо в поле комплексных чисел. Для случая уравнений 3-й и 4-й степеней эта теорема была установлена в XVI в. Тартальей, Кардано и другими: оказалось, что такие уравнения решаются посредством формул, подобных формуле квадратного уравнения, но значительно более сложных. В течение почти двух столетий длилось настойчивое изучение
128 |
МАТЕМАТИЧЕСКАЯ ЧИСЛОВАЯ СИСТЕМА |
гл. II |
общего уравнения 5-й и более высоких степеней, но все усилия разрешить их теми же методами оказались напрасными. Когда молодому Гауссу в его докторской диссертации (1799) удалось впервые доказать, что решения существуют, то это уже было крупнейшим успехом; правда, вопрос о возможности обобщить на случай степеней > 5 классические формулы, позволяющие находить корни с помощью рациональных операций и извлечения корней, оставался в то время открытым (см. стр. 138).
Теорема Гаусса утверждает, что, каково бы ни было алгебраическое уравнение вида (17), где n — целое положительное число, а коэффициенты a — действительные или даже комплексные числа, существует по крайней мере одно такое комплексное число a = c + di, что
f(a) = 0.
Число a называется корнем уравнения (17). Доказательство этой теоремы будет приведено в этой книге на стр. 289–291. Предположим пока, что теорема доказана, и выведем из нее другую теорему, известную под названием основной теоремы алгебры (было бы, впрочем, правильнее назвать ее основной теоремой комплексной числовой системы): всякий алгебраический полином степени n
f(x) = xn + an 1xn−1 |
+ . . . + a1x + a0 |
(18) |
− |
|
|
может быть представлен в виде произведения ровно n множителей:
f(x) = (x − a1)(x − a2) . . . (x − an), |
(19) |
где a1, a2, . . . , an — комплексные числа, корни уравнения f(x) = 0. Так,
например, полином
f(x) = x4 − 1
разлагается на множители следующим образом:
f(x) = (x − 1)(x − i)(x + i)(x + 1).
Что числа a являются корнями уравнения f(x) = 0, это очевидно из самого разложения (19), так как при x = ar один из множителей f(x), а следовательно, и сам полином f(x), обращается в нуль.
В иных случаях не все множители x − a1, x − a2, . . . полинома f(x) степени n оказываются различными; так, в примере
f(x) = x2 − 2x + 1 = (x − 1)(x − 1)
мы имеем только один корень, x = 1, «считаемый дважды», или «кратности 2». Во всяком случае, полином степени n не может разлагаться в произведение более чем n различных множителей вида x − a, и соответствующее уравнение не может иметь более n корней.
При доказательстве основной теоремы алгебры мы воспользуемся — не в первый раз — алгебраическим тождеством
xk − ak = (x − a)(xk−1 + axk−2 + a2xk−3 + . . . + ak−2x + ak−1), (20)
