Бусыгин

61

Приведенный вариант теоремы Куна-Таккера является широко распространенным и включен в стандартные курсы по оптимизации. К сожалению, предположения сделанные нами ранее не позволяют в полной мере опираться на эти результаты. Во-первых, данный вариант теоремы опирается на дифференцируемость целевой функции. Допуская некоторую нестрогость, мы часто будем предполагать выполнение этого свойства, никак это не обсуждая и обосновывая. Заинтересованный читатель сможет найти его вывод из исходных свойств предпочтений в работе Жерара Дебре – G. Debreu, Smooth preferences, Econometrica, 1972, Vol. 40 и Smooth preferences. A corrigendum, Econometrica, 1976, Vol. 44.38 Во-вторых, мы можем говорить лишь о квазивогнутости функции полезности, но никак не о вогнутости. Конечно, в случае, когда существует монотонно возрастающее преобразование исходной квазивогнутой функции полезности, переводящее ее в эквивалентную (с точки зрения предпочтений) вогнутую, мы можем воспользоваться приведенным вариантом теоремы. Однако, как было отмечено при обсуждении квазивогнутости, существуют квазивогнутые функции, которые не могут быть преобразованы в вогнутые, и применение изложенного варианта кажется недопустимым. Действительно, механическая замена условий вогнутости на более слабые условия квазивогнутости делают утверждение теоремы неверным. Для того, чтобы понять это, достаточно рассмотреть простой пример f(x)= x2, g1(x) = 1–x, g2(x) = x, X=Ê. Тем не менее, некоторый вариант теоремы КунаТаккера справедлив и в случае квазивогнутых функций. Приведем его для случая X=RK+ . Более общая версия теоремы для случая, когда X некоторое подмножество RK, можно найти в цитированной выше статье Кеннета Эрроу и Алена Энтховена “Квазивогнутое программирование” (Econometrica, V. 29(4), 779-800).

Теорема Куна-Таккера для квазивогнутых функций (Достаточное условие оптимальности)

Пусть f(x) дифференцируемая квазивогнутая функция от n-мерного вектора x, а g(x) дифференцируемая квазивогнутая вектор-функция, обе определенные при x>0. Пусть x^ и λ удовлетворяют условиям Куна-Таккера

1)f(x^)+λ g(x^) < 0;

2)x^ ( f(x^)+λ g(x^)) = 0;

3)λg(x^) = 0;

4)λ > 0

и выполнено одно из следующих условий:

1)fi(x^)< 0, по крайней мере, для одной переменной xi;

2)fi(x^) > 0, для некоторой переменной xi, такой, что в допустимом множестве, задаваемом ограничениями задачи, существует точка x*, в которой x*i > 0;

3)f(x^) ≠ 0 и f(x) – дважды непрерывно дифференцируема в окрестности точки x^;

4)f(x) – вогнутая функция.

Тогда x^ максимизирует f(x) при ограничениях g(x)>0, x>0.

Если, кроме того, при некотором x* >0 справедливо g(x*)> 0, и для каждого j выполнено одно из условий: либо 1) gj(x) вогнута; либо 2) для каждого x>0 верно gj(x) ≠ 0, то условия Куна-Таккера являются необходимыми и достаточными.

38 Идейно, данное свойство функции полезности получается в предположениях достаточной гладкости поверхности безразличия, получаемой на основании наших предпочтений.

61

62

Применим теперь эту теорему к рассматриваемой нами задаче потребителя в случае, когда X = ÊK+ . Рассмотрим вначале несколько вариантов условий на предпочтения, гарантирующих то, что условия Куна-Таккера определяют решение задачи потребителя. Одним из наиболее простых вариантов состоит в том, чтобы предположить условие 3, то есть неравенство градиента нулю и дважды непрерывную дифференцируемость функции полезности. Но мы рассмотрим также другой комплекс условий, который будет востребован нами в дальнейших рассуждениях.

Определение 15.

Квазивогнутая функция u(x) называется сильно квазивогнутой, если для каждого x из области определения zH(x)zÅ< 0 для каждого z такого, что z u(x) = 0 и z≠0, где H(.)– матрица вторых частных производных.

Предположим, что предпочтения агента представимы дважды непрерывно дифференцируемой сильно квазивогнутой, локально ненасыщаемой функцией полезности.

Пусть нашлись некоторые x^ и λ, которые удовлетворяют условиям Куна-Таккера:

1)u(x^) – λp<0;

2)( u(x^)–λp)x^ = 0;

3)λ(R –Ûpkx^k) = 0;

4)λ > 0.

Покажем, что при сделанных предположениях найдется такое благо i что u i(x^) > 0.

Рассмотрим вначале случай, когда найденное значение λ > 0. Тогда в силу 3) имеем Û pkx^ k= R . Откуда, используя 2), и тот факт, что R > 0 имеем u(x^)x^> 0. Последнее влечетui(x^) > 0 для некоторой переменной xi, такой, что в допустимом множестве существует точка x*, в которой x*i > 0 (существование такой точки очевидно в силу положительности цен и дохода).

Пусть теперь λ = 0. Тогда u(x^)x^ = 0. В силу квазивогнутости для любого числа 0<α<1 и любого потребительского набора x**, такого, что u(x**) > u(x^), справедливо: u(x^ + α(x**– x^))>min{ u(x^), u(x**)} = u(x^). Или

u(x^ + α(x**–x^)) – u(x^)

α >0.

Устремляя α к 0 имеем: u(x^)(x**–x^)>0. Так как u(x^)x^ = 0, то u(x^)x**>0 для каждого потребительского набора, строго предпочитаемого набору x^. Очевидно, что такие потребительские наборы найдутся в силу свойства локальной ненасыщаемости. С другой стороны из условия 1) имеем, что u(x^)x**<0. Таким образом, u(x^)x**= 0. Рассмотрим разложение функции u(.) в окрестности точки x^:

u(x^ + z) = u(x^) + u(x^)zÅ + zHzÅ +||z||2o(||z||2),

где H – матрица вторых частных производных функции u(.), а o – бесконечно малая величина при z стремящемся к нулю. Для любого z = x**– x^, где u(x**) > u(x^), имеем u(x**) = u(x^) + zHzÅ +||z||2o(||z||2) = u(x^) + ||z||2(||zz||H(||zz||)Å +o(||z||2)).

Непрерывная функция yHyÅ достигает своего максимума (M) и минимума (m) на сфере ||y||2= 1. В случае отрицательной определенности матрицы H справедливо, что m<M< 0. В

62

63

силу этого, найдется такая величина δ>0, что при ||y|| < δ будет |o(||y||2)| < | M | и, тем самым, yHyÅ+o < 0. В силу локальной ненасыщаемости функции u(.) в любой δ- окрестности точки x^ найдется строго лучшая точка x**, и, кроме того, в силу квазивогнутости матрица Гессе будет отрицательно полуопределена на векторах таких, что u(x^ )y=0. В качестве y возьмем вектор (x**– x^). Таким образом, имеем u(x**) < u(x^), что противоречит выбору точки x**.

Таким образом, вышеприведенные гипотезы гарантируют нам положительность множителя Лагранжа λ, и существование такого товара для которого ui′(x^) > 0 и, значит, выполнено условие 2 сформулированной выше теоремы.

Рассмотрим теперь необходимые условия оптимальности в задаче потребителя. По теореме Куна-Таккера (при выполнении условий регулярности, которые в данном случае эквивалентны тому, что не все цены равны нулю и доход строго положителен) существует множитель Лагранжа λ> 0 такой, что в оптимуме

Как показано выше, при сделанных нами предположениях множитель Лагранжа строго положителен. Кроме того, мы получили существование хотя бы одного блага с положительным объемом потребления. Для этого блага k и любого блага s исключая множитель Лагранжа из условий Куна-Таккера имеем:

В случае если благоs таково, что xs > 0 то это неравенство выполняется как равенство

Это свойство известно читателю из вводного курса микроэкономики и означает, что решение задачи потребителя характеризуется равенством предельной нормы замещения любых двух благ отношению цен этих благ. Так как λ > 0, то по условию дополняющей нежесткости теоремы Куна-Таккера получаем, что бюджетное ограничение должно выходить на равенство: px= R. Это второе условие первого порядка, которому должен удовлетворять оптимум рассматриваемой задачи.

Проиллюстрируем теперь применение достаточных условий оптимальности для нахождения функции спроса на примере.

Пример 9.

Пусть множество допустимых альтернатив X=ÊK+ и предпочтения потребителя предста-

63

64

Очевидно, что матрица H отрицательно определена. Таким образом, функция полезности u(x) является вогнутой. Также отметим, что u(x) – монотонна. Тем самым, мы подпадаем под условия теоремы Куна-Таккера и условия дополняющей нежесткости являются достаточными условиями оптимальности.

Функция Лагранжа для задачи потребителя с функцией полезности u(x)= x1 +a x2 имеет вид:

L(x, λ) = x1 +a x2 + λ(R – p1x1 – p2x2).

Условия Куна-Таккера (условия дополняющей нежесткости)

Данные условия выполнены только если x1>0, x2>0. Таким образом

Из первых двух уравнений имеем

Подставляя полученное выражение для x2 в бюджетное ограничение, получим

Легко видеть, что полученная нами функция спроса удовлетворяет всем свойствам функции спроса установленными в теореме 14. (Проверьте это самостоятельно!)

Перейдем теперь к рассмотрению другого важного понятия в теории потребительского выбора, а именно понятия непрямой функции полезности.

Определение 16.

Функция ν(p, R) = u(x(p, R)), где x(p, R) –решение задачи потребителя (отображение спроса) при ценах p и доходе R, называется непрямой функцией полезности.39

39 Непрямая функция полезности впервые рассматривалась в работе Antonelli, G.B., Sulla Teoria Matematica della Economia Politica, Pisa, 1886.

64

65

Естественно, область определения непрямой функции полезности это такие пары цен и доходов (p, R) при которых существует решение задачи потребителя. В нашем случае это такие пары (p, R), что выполнено p ÊK++ и R >infx Xpx.

Следующая теорема устанавливает основные свойства задачи потребителя в модели потребителя с фиксированным доходом.

Теорема 16. (Свойства непрямой функции полезности)

Пусть выполнены предположения Теоремы 14. Тогда

(1)функция ν(p, R) однородна нулевой степени по (p, R): ν(λ p, λR) = ν(p, R);

(2)функция ν(p, R) не убывает по доходу (ν(p,R ′) > ν(p,R) при R ′>R), причем строго возрастает по доходу, если предпочтения локально ненасыщаемы;

(3)функция ν(p, R) не возрастает по ценам (ν(p, R) < ν(p′, R) при p >p′), причем строго убывает по ценам, если предпочтения локально ненасыщаемы;

(4)функция ν(p, R) квазивыпукла по (p, R);

(5)если предпочтения потребителя выпуклы, то функция ν(p, R) непрерывна на множестве определения.

Доказательство:

(1)Однородность нулевой степени следует из определения непрямой функции полезности и однородности нулевой степени функции спроса x(p, R) (см. Теорему 14).

(2)Покажем, что ν(p, R) не убывает по R. Рассмотрим непрямую функцию полезности при двух разных уровнях дохода R′ и R, таких, что R′>R. Поскольку при R′> R бюджетное множество B(p, R′) содержит бюджетное множество B(p, R) (отметим, что случай B(p, R′)=B(p, R) не исключен), то по определению непрямой функции полезности имеем ν(p, R′)>ν(p, R).(Почему?) Предположим теперь, что предпочтения локально ненасыщаемы. Если бы при R′>R мы имели ν(p, R′)=ν(p, R), то наборы из x(p, R) принадлежали бы x(p, R′), но для них не выполнялся бы закон Вальраса, чего быть не может, значит должно выполняться строгое неравенство ν(p, R′) >ν(p, R).

(3)Доказательство данного пункта в целом повторяет доказательство предыдущего и оставляется читателю в качестве упражнения.

(4)Напомним, что функция f(x) называется квазивыпуклой, если функция –f(x) является квазивогнутой. Мы хотим показать квазивогнутость функции ν(p, R), т.е. что для любого 0<α<1 выполнено

ν(αp1 + (1 – α)p2, αR1 + (1 – α)R2) < max {ν(p1, R1), ν( p2, R2)}.

Пусть x — решение задачи потребителя при ценах pα= αp1 + (1 – α)p2 и доходе Rα = αR1 + (1 – α)R2, т.е. x x(pα, Rα). Очевидно, что x является допустимым либо при ценах p1 доходе R1, либо при ценах p2 и доходе R2. Действительно, если бы это было не верно, тогда выполнялось бы p1x >R1 и p2x >R2. Взяв первое неравенство с весом α, а второе неравенство с весом (1 – α) и сложив, получаем pαx >Rα. Противоречие с тем, что x x(pα, Rα). Таким образом, выполнено либо p1x < R1, либо p2x<R2. Без потери общности предположим, что p1x < R1. Из того, что ν(p1, R1) есть по определению значение целевой функции на оптимальном решении задачи потребителя при ценах p1 и доходе R1, следует что ν(p1, R1)>u(x), так как x — допустимое решение этой задачи. Тем более, должно выполняться и требуемое соотношение

65

66

u(x) =ν(pα, Rα) < max{ν(p1, R1), ν( p2, R2)}.

(5) В предположении строгой выпуклости предпочтений непрерывность непрямой функции полезности следует из определения и непрерывности функции x(p, R), которую мы доказали в Теореме 14. Доказательство в общем случае читатель может найти в книге В.

Гильденбранд, Ядро и равновесие в большой экономике, М.: Наука, 1986, стр. 31.

*

Проиллюстрируем понятие непрямой функции полезности на примере гомотетичных предпочтений.

Пример 7. (Продолжение)

Выше мы показали, что функция маршаллианского спроса однородна первой степени по доходу, т.е. x(p, R)=Rx(p, 1). Таким образом, ν(p, R)= u(x(p, R)) = u(Rx(p, 1)) = u(x(p, 1))R = a(p)R, где в качестве a(p) выступает u(x(p, 1)).

Пример 9. (Продолжение)

Непрямая функция полезности будет иметь вид:

Проверим теперь выполнение свойств непрямой функции полезности полученных нами в теореме 16.

Возрастание непрямой функции полезности по доходу очевидно в силу возрастания функции x.

1

Убывание непрямой функции полезности по ценам следует из того факта, что функции p1

Проверка квазивогнутости непрямой функции полезности достаточно громоздка, и мы ее проводить не будем. Желающие могут проделать ее самостоятельно.

Помимо введенных выше понятий отображения спроса и непрямой функции полезности важное место в микроэкономической теории занимает понятие хиксианского спроса.

Определение 17.

Пусть на X задана система неоклассических предпочтений, L+(x)={y X| y}x}– верхнее

K

лебеговское множество, отвечающее набору x. Тогда отображение h: Ê+ ×X→2X, определяемое формулой h(p, x)={ y L+(x)| py<pz z L+(x)}, называется

су (хиксианским спросом)40. В случае если h(p, x) – одноэлементное множество, то h(p, x) называется функцией спроса по Хиксу.41

40 Приведенное здесь определение хиксианского спроса не является классическим. В большинстве учебников задача поиска хиксианского спроса формулируется в терминах поиска набора, который дает заданный уровень полезности, а приведенный вариант определения зарезервирован для задачи определения монетарной функции полезности. Преимуществом введенного в тексте понятия является то, что оно последователь-

66

67

В случае если предпочтения представимы функцией полезности u:X→Ê, то отображение хиксианского спроса может быть найдено как решение параметрического семейства задач:

ph → minh u(h) > u(x),

h X,

каждая из которых обычно называется двойственной (взаимной) к соответствующей задаче потребителя (задаче поиска маршаллианского спроса).

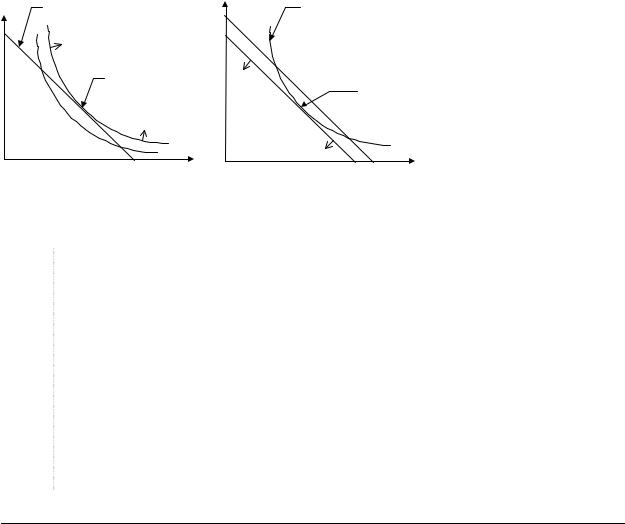
С содержательной точки зрения хиксианский спрос при заданных p и x это самый дешевый потребительский набор при заданных ценах p, среди всех наборов которые не хуже чем x. В то же время, маршаллианский спрос — это наилучший с точки зрения предпочтений индивидуума набор в бюджетном множестве. На Рисунке 10 в случае двух благ иллюстрируется разница в понятиях маршаллианского и хиксианского спросов.

маршаллианский спрос хиксианский

спрос

Рисунок 10 Маршаллианский и хиксианский спрос.

Следующая Теорема устанавливает основные свойства отображения (функции) хиксианского спроса.

Теорема 17. (Свойства хиксианского спроса)

Пусть p ÊK++, а потребитель описывается системой непрерывных неоклассических предпочтений. Тогда

(1)решение двойственной задачи потребителя существует, т.е. h(p, x) ≠ x X;

(2)если предпочтения потребителя выпуклы, тогда h(p, x) — выпуклое множество;

(3)если предпочтения потребителя строго выпуклы, то h(p, x) — непрерывная функция;

(4)отображение h(p, x) однородно нулевой степени по p, т. е. h(λp, x) = h(p, x);

(5)для каждого h h(p, x) справедливо u(h) = u(x);

(6)для любых p, p′ ÊK++, h h(p, x) и h′h(p′, x) справедливо (p′ - p)(h′ - h)<0.

но ложится в программу описания потребителя исходя только из свойств предпочтений, не используя понятия и термины которые могут быть сассоциированны с кардиналистским подходом.

41 Понятие хиксианского спроса появилось, и получила свое развитие, в работах Джона Хикса (Hicks, J. R.,

Value and Capital, Oxford: Claredon Press, русс. перевод Дж. Р. Хикс, Стоимость и Капитал, М.: Прогресс, 1993), Пола Самуэльсона (Samuelson, P., Foundations of Economic Analysis, Cambridge, Mass.: Harvard University Press, 1948) и Лайонеля Мак-Кензи (McKenzie, L., Demand Functions without a Utility Index, Review of Economic Studies, Vol. 25, 1957).

67

68

Доказательство:

Доказательство в общих чертах идет по схеме доказательства Теоремы 14 и оставляется читателю в качестве упражнения.

■

Обсудим свойство 6 данной теоремы. Пусть в некоторый момент времени в экономике были цены p, а в следующий момент времени изменилась цена одного из благ, для определенности первого, а цены всех остальных благ остались неизменными. В этом случае свойство 6 говорит, что должно выполняться неравенство ∆p1∆h1<0, т.е. если цена первого блага упала, то хиксианский спрос на первое благо не может упасть, он либо остается неизменным, либо возрастает. Оговоримся, что полученное неравенство (p′ - p)(h′ - h) < 0 более сильное условие, чем простое требование убывания спроса на k-ое благо по своей

цене. Это свойство мы будем называть законом спроса при компенсированном изменении

дохода по Хиксу. Оно в чем-то аналогично рассмотренному ранее закону спроса при компенсированном изменении дохода по Слуцкому. В дальнейшем мы вернемся к обоим этим свойствам потребительского спроса и достаточно подробно обсудим их взаимосвязь.

Обсудим теперь, как и в случае с маршаллианским спросом, необходимые и достаточные условия максимума задачи поиска хиксианского спроса. Предположим, как и ранее, что функция полезности дважды непрерывно дифференцируема, предпочтения удовлетворяют свойству локальной ненасыщаемости, выпуклы и, кроме того, p ÊK++. Несложно заметить, что при выполнении этих предположений целевая функция задачи поиска хиксианского спроса вогнута (выполнено условие 4) и, даже больше, целевая функция дважды непрерывно дифференцируема и не равна 0 (выполнено условие 3). В силу этого, условия КунаТаккера являются достаточными условиями оптимальности для потребительского набора

h^ такого что

1)– p + µ u(h^)<0;

2)(– p + µ u(h^))h^ = 0;

3)µ(u(h^) – u(x)) = 0;

4)µ > 0.

Пусть x = x( p, R) – решение задачи потребителя при ценах p ÊK++ и доходе R >0. Пусть также λ – множитель Лагранжа, отвечающий этому решению. Тогда, как несложно заметить, в случае если λ>0, множитель Лагранжа в задаче поиска хиксианского спроса µ ра-

1

вен λ.

Сформулированные условия являются также и необходимыми условиями оптимальности для этой задачи, если найдется такой потребительский набор h*, что u(h*)>u(x) (выполнение данного условия гарантировано свойством локальной ненасыщаемости) и градиент функции u(.) не равен 0.

Используя условия Куна-Таккера, найдем теперь функцию хиксианского спроса для случая рассматривавшегося нами в примере 9.

Пример 9. (Продолжение)

Хиксианский спрос является решением следующей задачи

p1h1 + p2h2 → minh h1 +a h2 > u(x), h>0.

68

69

Функция Лагранжа для этой задачи имеет вид:

L(h, µ) = –p1h1 – p2h2+ µ( h1 +a h2 – u(x)).

Условия Куна-Таккера могут быть выполнены только в случае, если h1>0, h2>0. Поэтому

Проиллюстрируем теперь свойства функции хиксианского спроса доказанные в теореме 17. То, что хиксианский спрос однороден нулевой степени по ценам очевидно, действи-

Покажем, что u(h(p, x)) = u(x). Подставив хиксианский спрос в функцию полезности, мы получим:

Аналогом непрямой функции полезности в двойственной задаче потребителя является функция расходов.

Определение 18.

Функция e(p, x) = ph, где h h(p, x) – хиксианский спрос при данных p и x, называется

функцией расходов (затрат).

Другими словами, функция расходов e(p, x) – значение целевой функции двойственной задачи в точке оптимума при данных p и x. Согласно определению, для каждого достижимого уровня полезности функция расходов указывает минимальный уровень расходов (дохода), обеспечивающий такой уровень полезности.

Теорема 18. (Свойства функции расходов)

Пусть выполнены предположения Теоремы 17. Тогда

(1)функция e(p, x) однородна первой степени по p: e(λ p, x) = λe(p, x);

(2)функция e(p, x) не убывает по ценам e(p′, x)< e(p, x) при p >p′);

(3)функция e(p, x) — вогнутая функция цен p;

(4)функция e(p, x) непрерывна;

(5)x } y e(p, x)>e(p, y);

Доказательство:

69

70

(1)Первый пункт утверждения следует из того, что решения двойственной задачи при векторе цен p и векторе цен λp совпадают.

(2)Пусть p′>p и p′≠p. Тогда ph(p′,x)> ph(p,x) = e(p,x). Но e(p′,x) = p′h(p′,x) > ph(p′,x). Заметим, что если h(p′,x)Þ0, то e(p′,x) > e(p,x).

(3)Мы должны показать, что для двух произвольных векторов p1 и p2 при 0< α < 1 вы-

полняется e(αp1 + (1–α)p2, x) > αe(p1, x) + (1–α)e(p2, x). Пусть h~— решение двойственной задачи при ценах pα=αp1 + (1–α)p2, т.е. h~ h(pα, x). Отметим, pαh~ = e(pα, x).

Допустимое множество {h X| y } x} не зависит от p, поэтому потребительский набор h~ допустим в двойственной задаче как при ценах p1, так и при ценах p2. Из определения

функции расходов и допустимости h~ имеем e(p1, x)< p1h~ и e(p2, x) < p2h~. Отсюда

αe(p1, x) + (1 – α)e(p2, x)<pαh~ = e(pα, x).

(4) Доказательство непрерывности оставляем читателю в качестве упражнения. Заметим только, что непрерывность следует из того, что (а) функция расходов вогнута как функция цен и (б) любая вогнутая функция непрерывна во внутренности своей области определения.

(5 ) Докажем, что из x } y следует e(p, x)>e(p, y). Так как x } y, то все потребительские наборы допустимые в двойственной задаче при наборе параметров (p, x) являются допустимыми в задаче при наборе параметров (p, y). В том числе, допустимыми являются и наборы, принадлежащие h(p, x), а это и означает что e(p, x)>e(p, y).

(5 ) Докажем, что из e(p, x)>e(p, y) следует x } y. Предположим противное, то есть y } x. Значит e(p, y)=e(p, x) (Почему?). Значит h(p, y) h(p, x). Возьмем h~ h(p, y). В силу непрерывности предпочтений и того, что X– выпуклое множество и 0 X получаем суще-

ствование такого числа α<1, что αh~ } x. В этом случае p(αh~) = αe(p, y) < e(p, x), что противоречит определению e(p, x).

■

На основании пункта (5) можно говорить о функции e(p, x), как о функции полезности, которая представляет исходную систему неоклассических предпочтений. Это свойство одно из самых важных свойств функции расходов и будет поставлено во главу угла при обсуждении вопроса о восстановлении предпочтений по наблюдаемой функции спроса.

Проиллюстрируем теперь нахождение функции расходов.

Пример 9. (Продолжение)

Найдем функцию расходов e(p, x) для данного потребителя. Как было показано выше,

p u(x)

функция хиксианского спроса для рассматриваемого потребителя равна h(p, x)=((p2+a2p

2 1

ap u(x)

)2, ( p2+a1 2p1 )2). Из определения функции расходов имеем:

На примере данной функции проиллюстрируем выполнение свойств, доказанных в теореме 18.

Покажем, что полученная функция однородна первой степени по ценам.

70