
- •ОГЛАВЛЕНИЕ
- •ВВЕДЕНИЕ
- •1.1. Основные понятия и определения теории вероятностей
- •1.2. Функции распределения вероятностей случайной величины
- •1.3. Числовые характеристики случайных величин
- •1.5. Случайные процессы и их основные статистические характеристики
- •1.6. Корреляционные функции случайных процессов
- •1.7. Спектральные плотности случайных процессов
- •1.9. Прохождение дискретного случайного процесса через дискретное динамическое звено первого порядка
- •ЗАДАЧИ
- •2. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- •2.1. Общие понятия и определения
- •2.2. Простейшие оценки
- •2.3. Интервальные оценки. Доверительный интервал
- •2.4. Проверка статистических гипотез о параметрах распределения
- •2.5. Критерии согласия
- •2.6. Последовательный анализ
- •2.7. Особенности статистического вывода
- •2.8. Статистики и измерения стационарного случайного процесса
- •2.9. Оценка корреляционной функции
- •2.10. Оценка спектральной плотности
- •ЗАДАЧИ
- •3. МОДЕЛИ ОБЪЕКТОВ УПРАВЛЕНИЯ
- •3.1. Средства и этапы описания объектов управления
- •3.2. Характеристика моделей объектов управления
- •3.3. Динамические модели объектов управления
- •3.4. Преобразование и исследование динамических моделей
- •3.5. Статические модели
- •3.6. Графическое представление статических моделей
- •3.7. Пример описания объекта управления
- •4. МЕТОДЫ ИДЕНТИФИКАЦИИ
- •4.1. Дисперсионный анализ
- •4.2. Метод регрессионного анализа
- •4.3. Рекуррентные алгоритмы идентификации линейных моделей
- •4.5. Идентификация параметров динамических моделей
- •4.6. Сглаживание временных рядов
- •ЗАДАЧИ
- •5. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
- •5.1. Общие требования к плану эксперимента
- •5.2. Полный факторный эксперимент
- •5.3. Дробный факторный эксперимент
- •5.4. Планы для квадратичных моделей
- •ЗАДАЧИ
- •СПИСОК ИСПОЛЬЗУЕМЫХ АББРЕВИАТУР И ОБОЗНАЧЕНИЙ

1.3.Числовые характеристики случайных величин
Интегральная или дифференциальная функции распределения вероятностей являются исчерпывающими вероятностными характеристиками случайной величины. Однако часто достаточно знать лишь некоторые числовые параметры, характеризующие отдельные существенные черты распределения случайной величины. К ним относят.
Математическое ожидание непрерывной случайной величины X , возможные значения которой принадлежат всей оси ОХ, определяется выражением
M X m |
|
|
|
xf (x)dx , |
(1.16) |
||
|
x |
|
|
соответственно для дискретной случайной величины
M X x p . (1.17)
i i
Ввыражениях (1.16) и (1.17) предполагается, что интеграл и сумма
сходятся абсолютно.
Если X – случайная величина, то произвольная функция g( X ) , также является случайной величиной. Математическое ожидание этой функции
|
|
|
|
|
|
M g( X ) |
|
|
|
|
|
|
|
|
|
|
g(x) f (x)dx , ( X – непрерывна); |
(1.18) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M (gX ) g(x) p(x) , ( X – дискретна). |
(1.19) |
|||
|
|
|
|
|
|
|
x |
|
|
|
Дисперсия случайной величины X равна |
|
|||||||||
D X |
|
|
|
|
|
|
|
|
||
|
|
|
(x m ) |
f (x)dx , ( X – непрерывна); (1.20) |
||||||
|
M X m |
|
||||||||
|
|
|
x |
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p(x) , ( X – дискретна). |
(1.21) |
D X x |
M X mx x mx |
|||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||||||
Величину |
– называют средним квадратическим отклонением |
|||||||||
|
|
|
|
x |
x |
|
|
|
|
|
(стандартом) случайной величины X . |
|
|
|
|||||||
m |
x |
, – центр и степень рассеяния случайной величины X . |
|
|||||||
|
x |
|
|
|
|
|
|
|
|
|
Некоторые свойства
17
M c c ; |
D c , c константа; |
|
|||
M cX cM X ; D cX c D X ; |
|
||||
M a bX a bM X ; D a bX b D X ; |
|
||||
M X X |
... X n M |
X M X ... M X |
|||
D X X |
|
...X n |
D X |
D X ... D X n |
; |
M X X |
... X n |
M X M X ... M X n . |
|
||
здесь X , X ,...,X n – взаимно независимые случайные величины.
(1.22) n ;
Для характеристики вариабельности случайной величины используют
коэффициент вариации |
|
|
x |
. |
|
|
||
|
m |
|
|
x |
|
Значения mx и x используются для центрирования случайной вели-
чины
|
|
X X mx |
(1.23) |
и нормирования (стандартизации) случайной величины
|
|
|
|
X mx |
|
|
|
|
|
|
|
|
x |
. |
|
|
|
(1.24) |
|||
|
|
|
|
|
|
|||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Очевидно, что M X |
, M x |
, D x |
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
Кроме перечисленных, имеются и другие числовые характеристики: медиана, мода, размах, коэффициенты асимметрии, эксцесса и др.[1, 2].
1.4.Многомерные распределения вероятностей
Часто для описания практической ситуации необходимо использование нескольких случайных величин X , X ,...,X n . Этот набор действительных
случайных величин представляет значение n -мерной случайной величины X X , X ,...,X n . В этом случае говорят о системе случайных величин или
n-мерном случайном векторе. Каждое элементарное событие может рассматриваться как результат сложного испытания, состоящего в измерении всех величин X , X ,...,X n , и интерпретироваться как точка n-мерного простран-
ства или вектор. Каждая из величин X , X ,...,X n является случайной величи-
ной (одномерной). Например, если эксперимент повторяется n раз, то его результаты удобно рассматривать как n случайных величин.
18

Распределение системы двух случайных (координат) величин X |
и X |
||||||||
или двумерного случайного |
вектора |
X X , X |
задается интегральной |
||||||
функцией совместного распределения |
|
|
|
|
|
||||
|
|
F x , x P X x , X x . |
(1.25) |
||||||
Функция F x , x имеет следующие основные свойства: |
|
||||||||
|
|
|
F x , x , F( , ) , F( , ) ; |
||||||
|
|
|
F x , , F , x ; |
|
|||||
|
|
|
F x , x - неубывающая функция. |
|
|||||
Вероятность попадания в прямоугольную область равна (рис. 1.6). |
|
||||||||
P a x b,c x d F |
b, d F a, d F b,c F a,c |
|
|||||||
|
x |
2 |
(a,d) |
(b,d) |
|
|
|
||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(b,c) |
|
|
|
|
|
|
(a,c) |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
x1 |
|
|||
Рис. 1.6. К определению вероятности попадания в прямоугольную область
Если функция F x , x достаточно гладкая, то ее можно продифференцировать и получить двумерную плотность вероятностей
f (x , x ) F (x , x ) ,
обладающую следующими свойствами:
|
|
|
|
f x , x ; |
|
|
|
|
|
||
|
|
|
|
|
f x , x dx dx ; |
|
|
|
|||
|
|
|
|
|
x |
x |
|
F x , x |
f x , x |
|
|
dx dx . |
|||
|
|
|
|
(1.26)
(1.27)
Вероятность события, что случайные величины X и X попадут в некоторую область равна
19
P X , X f x , x dx dx . |
(1.28) |
Геометрически вероятность соответствует относительному объему тела, ограниченного снизу областью , сверху функцией f x , x .
Две случайные величины X и X называются независимыми, если их
совместная функция распределения является произведением индивидуальных функций плотностей вероятности
|
f x , x f x f x , |
(1.29) |
|
|
|
|
|
где f x x , x dx , f x f x , x |
dx . |
|
|
|
|
|
|
Аналогично понятию условной вероятности может быть введено поня- |
|||
тие условного распределения случайной величины X при условии, что ве- |
|||
личина X приняла некоторое конкретное значение a |
|
||
|
f x | a f x | X a f x , a / f a . |
(1.30) |
|
Геометрически |
она представляет |
кривую от сечения поверхности |
|
f x , x плоскостью параллельной оси |
x , и проходящей через точку |
a и |
|
нормированную множителем / f a , чтобы удовлетворить условию |
|
||
|
|
|
|
|
f x , x dx . |
|
|
|
|
|
|
Для независимых случайных величин X и X |
|
||
|
f x | a f x ; f x | a f x . |
(1.31) |
|
Среди числовых характеристик многомерных распределений выделим (на примере двумерного) следующие.
Математические ожидания самих случайных величин (центр рассея-
ния)
|
|
|
|
|
|
|
|
|
|
|
mx |
|
x f x , x dx dx x f x dx , |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.32) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
dx . |
|
||||
|
|
mx |
|
x f x , x dx dx x f x |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Математическое ожидание некоторой функции g X , X |
|
|
|
|||||
|
|
|
|
|
для непрерыв- |
|
|
|
|
g x , x f x , x dx dx |
|
|
|
||||
|
ных, |
|
|
(1.33) |
||||
M g X , X |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
g x , x p x , x |
для дискретных. |
|
|
|||||
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
||
Центральные моменты второго порядка: дисперсии случайных величин
20

|
|
|
|
|
|
f x dx , |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
x |
|
x mx |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.34) |
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x mx |
|
f |
x dx , |
|
|
|
||
x |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
и ковариацию случайных величин X |
и |
X , или корреляционный момент, |
|||||||||
или смешанный момент второго порядка |
|
|
|
|
mx . |
|
|
||||
cov X , X M X mx X |
(1.35) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Иначе |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cov X , X M X X mx mx |
|
|
x x f x , x dx dx |
mx |
mx |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
.(1.36) |
|
Значение корреляционного момента служит определенной мерой зави- |
|||||||||||
симости между X и |
X . Для |
независимых |
случайных |
величин |
|||||||
cov X , X . Удобнее в качестве меры взаимозависимости случайных величин использовать коэффициент корреляции (безразмерный параметр)
X , X cov X , X . (1.37)
x x
По своему физическому смыслу коэффициент корреляции является простейшей характеристикой статистической связи, характеризующей лишь степень линейной зависимости X и X .
Используя условные функции распределения, можно ввести условное математическое ожидание и условную дисперсию
|
|
|
|
M X | a x f x | a dx , |
(1.38) |
||
|
|
|
|
|
|
f x | a dx . |
|
D X | a x mx |
|
(1.39) |
|
|
|
|
|
|
|
|
|
Многие понятия, введенные для совокупности двух случайных величин, обобщаются на n -мерный случай. Например, математическое ожидание функции n -переменных
|
|
|
M g X ,...,X n |
|
... g x ,...,xn f x ,...,xn dx dx ...dxn . (1.40) |
|
|
|
Среди распределений выделим двумерное нормальное распределение, которое задается функцией плотности распределения вероятностей вида
f x , x |
|
|
|
|
|
|
|
x mx T c x mx |
|
|
|
|
|
|
|
e |
|
, |
(1.41) |
||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
где
21
x m |
x |
|
|
mx |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
– вектор-столбец; |
|
|||||||
|
|
|
m |
|
|
||||||||||
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
x |
x |
|
|
|
|
|
|
|||
x |
|
|
|
|
|
|
|
|
|||||||
c |
|
|
|
|
|
|
|
– корреляционная матрица; |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– определитель корреляционной матрицы. |
||||||||||
| c | x |
x |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Степень рассеяния двух случайных величин X и |
X характеризуется |
||||||||||||||
площадью эллипса, равного |
|
|
|
|
. Следовательно, чем больше , |
||||||||||
| c | x |
x |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тем меньше площадь.
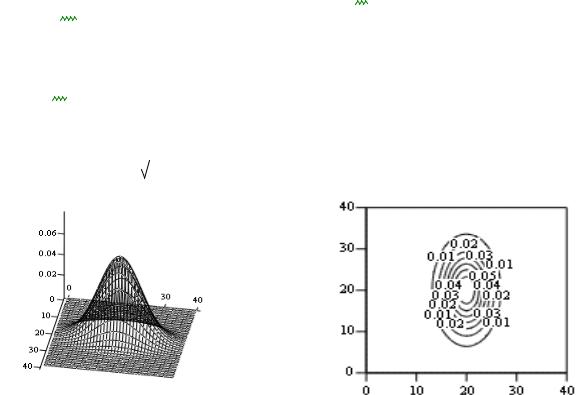
Графики функций (1.41) и ее сечения, линии равной плотности распределения вероятностей, представлены на рис. 1.7 и рис. 1.8.
n 40 |
i 0 n |
|
x1i 5 0.3 i |
|
|
j 0 n |
x2j 4 0.3 j |
||
mx1 1 |
mx2 2 |
x1 1 |
||
|
|
x1 |
2 |
x1 x2 |
|
|
C |
|
|
|
|||
|
|
|
|
|||
|
|
|
|
x2 2 |
|
|
|
|
|
|
|||
|
x1 |
x2 |
|
|||
0
x2 2
c x1 2 x2 2 1 2
C1 C 1
|
|
|
|
1 |
|
|
|
|
|
|
x1i mx1 |
|
||
S |
i j |
max |
x1 |
|
mx1 |
x2 |
|
mx2 |
C1 |
|
||||
|
|
i |
j |
|||||||||||
|
|
|
2 |
|
|
|
x2j mx2 |
|
||||||
|
|
|
|
|
|
|
|
|||||||
Mi j |
1 |
|
|
|
exp Si j |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
c |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M
a) |
б) |
Рис. 1.7. Двумерное нормальное распределение для ρ 0 : |
|
M
а) функция плотности распределения вероятности; б) ее линии равного уровня
22
n 40 |
|
|
i 0 n |
|
x1i 5 0.3 i |
|
|
||
|
|
|
|
j 0 n |
|
x2j 4 0.3 j |
|
|
|
mx1 1 |
|
|
|
mx2 2 |
|
0.5 |
|
|
|
x1 |
1 |
|
|
|
x2 2 |
|
c x1 2 x2 2 1 2 |
||
|
|
x1 |
2 |
x1 x2 |
|
||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
C |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
x2 2 |
C1 |
C |
||
|
x1 |
x2 |
|
|
|||||
|
|
|
|
1 |
|
|
|
|
|
|
x1i mx1 |
|
||
S |
i j |
max |
x1 |
|
mx1 |
x2 |
|
mx2 |
C1 |
|
||||
|
i |
j |
||||||||||||
|
|
|
2 |
|
|
|
x2j mx2 |
|
||||||
|
|
|
|
|
|
|
|
|||||||
Mi j |
1 |
|
|
exp Si j |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||
2 c |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
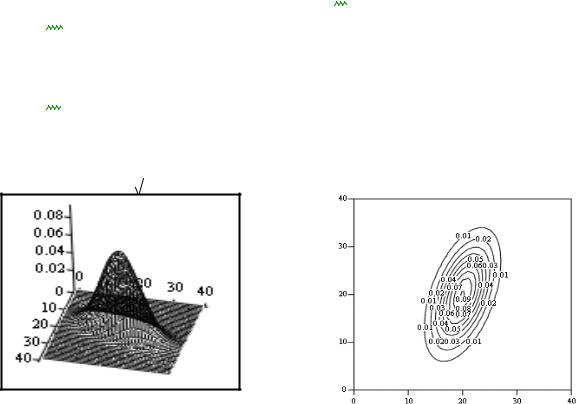
M
а) б)
Рис. 1.8. Двумерное нормальное распределение для 0.5 :
а) функция плотности распределения вероятности; б) ее линии равного уровня
M
Каждая из двух случайных величин, распределенных в совокупности по двумерному нормальному закону, также распределена нормально безотносительно тому, являются ли эти случайные величины независимыми. Обратное утверждение неверно, совместное распределение двух случайных величин, каждая из которых распределена нормально, не обязательно будет нормальным (не путать с суммой двух случайных величин). ЕслиX , X , то для нормального распределения некоррелированность озна-
чает одновременно и их независимость
f x , x f x f x .
Условное распределение f x | a также нормально с параметрами:
23
