
- •ОГЛАВЛЕНИЕ
- •ВВЕДЕНИЕ
- •1.1. Основные понятия и определения теории вероятностей
- •1.2. Функции распределения вероятностей случайной величины
- •1.3. Числовые характеристики случайных величин
- •1.5. Случайные процессы и их основные статистические характеристики
- •1.6. Корреляционные функции случайных процессов
- •1.7. Спектральные плотности случайных процессов
- •1.9. Прохождение дискретного случайного процесса через дискретное динамическое звено первого порядка
- •ЗАДАЧИ
- •2. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- •2.1. Общие понятия и определения
- •2.2. Простейшие оценки
- •2.3. Интервальные оценки. Доверительный интервал
- •2.4. Проверка статистических гипотез о параметрах распределения
- •2.5. Критерии согласия
- •2.6. Последовательный анализ
- •2.7. Особенности статистического вывода
- •2.8. Статистики и измерения стационарного случайного процесса
- •2.9. Оценка корреляционной функции
- •2.10. Оценка спектральной плотности
- •ЗАДАЧИ
- •3. МОДЕЛИ ОБЪЕКТОВ УПРАВЛЕНИЯ
- •3.1. Средства и этапы описания объектов управления
- •3.2. Характеристика моделей объектов управления
- •3.3. Динамические модели объектов управления
- •3.4. Преобразование и исследование динамических моделей
- •3.5. Статические модели
- •3.6. Графическое представление статических моделей
- •3.7. Пример описания объекта управления
- •4. МЕТОДЫ ИДЕНТИФИКАЦИИ
- •4.1. Дисперсионный анализ
- •4.2. Метод регрессионного анализа
- •4.3. Рекуррентные алгоритмы идентификации линейных моделей
- •4.5. Идентификация параметров динамических моделей
- •4.6. Сглаживание временных рядов
- •ЗАДАЧИ
- •5. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
- •5.1. Общие требования к плану эксперимента
- •5.2. Полный факторный эксперимент
- •5.3. Дробный факторный эксперимент
- •5.4. Планы для квадратичных моделей
- •ЗАДАЧИ
- •СПИСОК ИСПОЛЬЗУЕМЫХ АББРЕВИАТУР И ОБОЗНАЧЕНИЙ
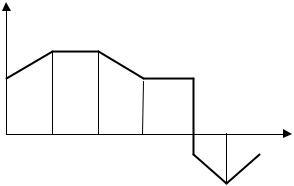
Другие примеры возмущений волновой структуры: z(t) c ,
z(t) c c e t ,
z(t) c c sin t c cos t c sin t c cos t;
z1 (t)
0 |
t1 |
t2 |
t3 |
t4 |
t5 |
t |
Рис. 3.3. Полудетерминированная кусочно-линейная возмущающая среда
3) стохастическую возмущающую среду, когда изменение вектора z(t) носит случайный характер, т.е. z(t) есть случайный процесс. При этом ОУ
находится в стохастической возмущающей среде. На практике широко используют представления вектора z(t) в виде многомерного случайного про-
цесса, как реакцию динамической системы на действие белого шума; 4) целенаправленную возмущающую среду, когда «выбор» возмуще-
ния z(t) осуществляется средой (противником) в соответствии с некоторой
целью, не всегда совпадающей с целью управления. Система управления находится в конфликтной среде.
Природа вектора ситуации w(t) может быть самой разнообразной. Так
он может быть обусловлен действием ошибок измерения векторов y, z, u вариацией (изменением) параметров объекта (шум объекта), влиянием неучтенных, неконтролируемых воздействий и т.д.
Выходные переменные yi (t) могут отражать состояние объекта управ-
ления, т.е. они являются наблюдаемыми переменными состояния, либо отражать эффективность управления, являясь экономическими показателями. В общем случае вектор y можно разбить на блоки, отражающие как наблюдаемые переменные состояния, так и показатели процесса управления.
3.3.Динамические модели объектов управления
Всоответствии с приведенной классификацией (см. рис. 3.2) рассмот-
105

рим динамические модели.
Нелинейные динамические объекты управления. В пространстве со-
стояний описание имеет вид |
|
|
|
x f x,u, z, w,t , |
(3.5) |
где f , |
y g x,u, z, v,t |
|
g( ) – вектор-столбцы нелинейных зависимостей, |
v(t) – вектор |
|
ошибок измерений.
Присутствие в правой части уравнений времени t свидетельствует о нестационарности ОУ. Первое уравнение системы (3.5) называют уравнением состояния, а второе – уравнением наблюдения.
Структурная схема нелинейной, нестационарной, стохастической, непрерывной, динамической системы, отвечающей уравнениям (3.5) и начальным условиям по состоянию x(0) , приведена на рис. 3.4.
|
z |
|
|
|
|
|
w |
|
|
v |
t |
|
t |
|
x(0) |
||
|
|
|
|
||
u |
x |
|
|
x |
y |
|
t |
|
|
||
|
|
|
|
|
|
|
f (x,u,z,w,t) |
( )dτ |
|
f (x,u,z,v,t) |
|
|
|
0 |
|
|
|
|
Рис. 3.4. Структурная схема нелинейного динамического ОУ |
|
|||
Нелинейные статические звенья структурной схемы (см. рис. 3.4) представлены двойными линиями, а динамические свойства – интегрирующим звеном, двойными стрелками отмечена многомерность переменных. Это наиболее общий случай и в нем отмечено безынерционное влияние вектора u(t)
и z(t) непосредственно на выходные переменные y(t) . На практике это
встречается крайне редко. Зачастую нелинейные объекты представляют в виде последовательного включения линейных динамических звеньев и нелинейного безынерционного (статического) преобразования.
Так для объектов первого рода
106

u |
|
|
x Ax B |
|
|
|
|
(3.6) |
z |
||
|
|
|
y g(x,t) v |
|
|
безынерционное преобразование включено после линейного динамического звена (рис. 3.5).
Здесь
|
a |
a |
... |
a |
|
|
|
|
|
|
n |
||
A |
a |
a |
... |
a n |
||
... ... |
... |
... |
||||
|
||||||
|
|
|
|
|
|
|
|
|
an |
... |
|
|
|
|
an |
ann |
||||
b |
b |
... |
b |
|
||
|
|
|
|
,m r |
||
b |
b |
... |
b ,m r |
|||
B |
|
|
... |
... |
|
|
... ... |
||||||
|
|
|
|
|
|
|
b |
b |
... |
b |
|
||
|
n |
n |
|
n,m r |
||
–основная матрица коэффициентов (параметров), матрица системы, матрица состояния;
–расширенная матрица коэффициентов (параметров) связи со входом, входная матрица, матрица управления.
z |
|
x(0) |
|
t |
|
u |
x |
|
x |
|
v |
t |
|
y |
|||
B |
|
( )dτ |
|
g (х,t ) |
|
|
|
|
|||
|
|
0 |
|
|
|
|
|
A |
|
|
|
Рис. 3.5. Структурная схема нелинейного динамического объекта первого рода
Для объектов второго рода безынерционное нелинейное преобразование включено перед динамическим звеном и имеет следующее описание
g g(u, z, x Ax g y Cx v
t)
, (3.7)
где
107

c |
c |
... |
c |
|
|
|
|
|
n |
|
|
c |
c |
... |
c n |
– матрица коэффициентов (параметров) связи с |
|
c |
|
... |
... |
выходом (матрица наблюдения). |
|
... ... |
|||||
|
|
|
|
|
|
|
c p |
... |
|
|
|
c p |
c pn |
|
|||
Структурная схема нелинейного, нестационарного, стохастического, непрерывного, динамического объекта второго рода (3.7) представлена на рис. 3.6.
Отметим, что аналитических методов решения уравнений (3.5), (3.6) и (3.7) не существует. Для их анализа прибегают к моделированию на ЭВМ.
Линейные динамические объекты управления. Система уравнений, опи-
сывающая поведение линейной нестационарной стохастической непрерывной системы имеет вид
u |
H (x,t)w |
|
|
|
x A(t)x B(t) |
|
|
|
|
|
|
, |
(3.8) |
|
z |
|
|
||
y C(t)x v |
|
|
|
|
|
|
|
|
где A(t) , B(t) , C(t) – матрицы коэффициентов (параметров), изменяющиеся во времени и обуславливающие нестационарность объекта; H (x,t) – матрица
коэффициентов (параметров), зависящая от времени и от переменных состояния объекта, обуславливает зависимость параметров объекта от его состояния (внутренний шум объекта).
|
z |
|
x(0) |
v y |
u |
g |
x |
x |
|
g(u,z,t) |
|
t |
|
|
|
|
( )dτ |
C |
|
|
|
|
0 |
|
|
t |
|
|
|
|
|
|
A |
|
Рис. 3.6. Структурная схема нелинейного динамического объекта второго рода
Системе уравнений (3.8) соответствует структурная схема (рис. 3.7). Линейный стационарный детерминированный динамический объект
описывается системой уравнений
108

x Ax Buu B z z |
. |
(3.9) |
|
y Cx |
|
||
|
|
|
|
Решение системы уравнений (3.9) имеет вид |
|
||
t |
|
t |
|
x(t) Ф(t)x(0) Ф(t τ)Bu u(τ)dτ Ф(t τ)B z z(τ)dτ |
|
||
0 |
|
0 |
(3.10) |
t |
|
t |
|
|
|
||
y(t) CФ(t)x(0) C Ф(t τ)Bu u(τ)dτ C Ф(t τ)B z z(τ)dτ, |
|
||
0 |
|
0 |
|
где Ф(t) e At – фундаментальная матрица, или матрица Коши.
|
t |
w |
|
|
|
|
|
|
|
|
|
|
|
|
t |
H(х,t) |
|
|
|
|
z |
|
|
x(0) |
t |
|
|
|
|
|
v |
|||
u |
|
x |
|
|
|
|
|
tt |
x |
|
y |
||
B(t) |
|
|
C(t) |
|||
|
|
|
( )dτ |
|
||
|
|
|
|
( )dτ |
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
A(t) |
|
|
Рис. 3.7. Структурная схема линейного нестационарного стохастического динамического объекта управления
Общих аналитических методов вычисления фундаментальной матрицы не существует. Для получения аналитического решения прибегают к разложению фундаментальной матрицы Ф(t) в ряд, а так же переход к канониче-
ской форме уравнений состояния с диагональной матрицей состояния и использования преобразования Лапласа. Чаще для решения систем вида (3.9) применяют методы численного интегрирования, реализуемые на ЭВМ. И конечно, так же, как и для нелинейных систем, универсальным методом анализа линейных динамических систем является метод моделирования на ЭВМ с использованием, например, системы инженерных и научных расчетов Matlab.
Дискретные объекты управления. Системы с дискретным временем описывают разностными уравнениями. Так, нелинейная, нестационарная, динамическая система с дискретным временем имеет вид
109
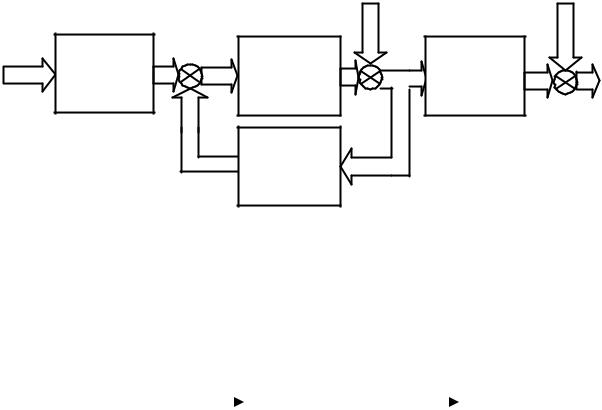
x(k 1) f x(k),u(k),z(k),k , |
(3.11) |
|
y(k) g x(k),k |
|
|
где k – дискретное время.
Линейная динамическая система с дискретным временем описывается уравнениями
x(k 1) Ax(k) Bu(k) |
(3.12) |
|
y(k) Cx(k) v(k) |
|
|
|
|
|
ией соответствует структурная схема (рис. 3.8).
Всистеме (3.12) обозначения матриц A, B,C соответствуют обозначе-
ниям непрерывных систем (3.6), однако численные значения элементов этих матриц отличаются от значений элементов непрерывной системы.
Модели «вход-выход». Обобщенно их можно представить структурной схемой (рис. 3.9), где u(t),u( p) – входное воздействие и его изображение,
y(t), y( p) – выходная переменная и ее изображение, W ( p), (t) – передаточная и весовая функция динамического объекта управления.
|
|
x(0) |
|
u(k ) |
x(k 1) |
v(k) |
|
x(k) |
|||
|
Iz 1 |
||
B |
C |
||
|
|
y(k) |
|
|
A |
|
Рис. 3.8. Структурная схема линейного стационарного динамического объекта с дискретным временем в пространстве состояний
Вот некоторые часто используемые в классической теории управления разновидности этих моделей.
|
u(t) |
W ( p) |
y(t) |
|||
|
|
|
|
|
||
|
|
|
(t) |
|
|
|
u( p) |
y( p) |
|||||
|
||||||
|
|
|
|
|
|
|
Рис. 3.9. Структурная схема модели «вход-выход»
110

Передаточная функция объекта управления относительного скалярного входа и выхода
|
|
|
W ( p) |
y( p) |
|
b |
b p ... b |
|
pm |
|
B( p) |
|
||||
|
|
|
|
0 |
1 |
m |
|
|
. (3.13) |
|||||||
|
|
|
u( p) |
1 a p ... a |
n |
pn |
A( p) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
Ей соответствует частотная передаточная функция |
|
|
|
|
|
|||||||||||
|
b b ( j ) ... b |
|
( j )m |
U ( ) jV ( ) A( )e j ( ) , |
|
|
||||||||||
W ( j ) |
|
|
m |
|
|
|
(3.14) |
|||||||||
a ( j ) ... a |
n |
( j )n |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где A( ) W ( j ) 
 U ( ) V ( ) – амплитудная частотная функция,
U ( ) V ( ) – амплитудная частотная функция,
( ) arctg V ( ) i , i , , – фазовая частотная функция.
U ( )
Коэффициент усиления статической модели системы (3.13)
|
K W ( ) |
b |
. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Если на вход ОУ действует и управление u(t) , и возмущение z(t), изо- |
||||||||||||
бражение выходной величины можно представить в виде |
|
|
|
|
||||||||
y( p) W1( p)u( p) W2 ( p)z( p) . |
(3.15) |
|||||||||||
Дискретная передаточная функция |
|
|
|
|
|
|
|
|
|
|||
|
y(z) |
b |
b z ... b |
z m |
|
B(z ) |
||||||
W (z) |
|
|
|
|
|
m |
|
|
, (3.16) |
|||
u(z) |
a z |
... a |
n |
z n |
A(z ) |
|||||||
|
|
|
|
|
|
|
|
|
|
|||
где параметры (коэффициенты) b ,b ,...,bm ,a ,a ,...,an численно отличны от
значений параметров модели (3.13), даже если описывают свойства одного объекта. Коэффициент усиления импульсной статической системы (3.16)
K lim W (z) |
b0 b1 |
... bm |
. |
||||||
1 a1 |
|
||||||||
|
|
|
z 1 |
|
|
... an |
|
||
Передаточной функции (3.13) соответствует дифференциальное урав- |
|||||||||
нение вида |
|
|
|
|
|
|
|
|
|
a |
n |
yn (t) a |
n |
yn (t) ... a y(t) y(t) |
|||||
|
|
|
|
|
|
(3.17) |
|||
b |
um (t) b |
|
um (t) ... b u |
||||||
|
(t) b u(t), |
||||||||
|
|
m |
|
m |
|
|
|||
с теми же коэффициентами, что и в выражении (3.13).
Передаточной функции (3.16) соответствует разностное уравнение
y(k) a y(k ) ... an y(k n) |
(3.18) |
|
b u(k) b u(k ) ... bmu(k m), |
||
|
||
с теми же коэффициентами, что и в выражении (3.16). |
|
|
Для нулевых начальных условий можно воспользоваться интегралом |
||
Дюамеля (интегралом свертки) |
|
|
111
