
Механика практикум_уч.пособие
.pdfАбсолютно неупругий удар.
При абсолютно неупругом ударе кинетическая энергия полностью или частично переходит во внутреннюю энергию, после удара тела движутся с одинаковой скоростью или покоятся.
Законы сохранения импульса и момента импульса принимают вид:
m1v1 m2 v2 m1 m2 u
J1 1 J2 2 J1 J2
Количество тепла, выделившегося при ударе, или работа, затраченная на неупругую деформацию тел, равна уменьшению кинетической энергии системы.
Q A Wk II Wk I
В частности, при взаимодействии материальных точек или поступательно движущихся твердых тел
m v 2 |
|
m v 2 |
|
|
|
|
2 |
|
|||
|
1 |
1 |
|
2 |
2 |
|
|
m1 |
m2 u |
|
|
Q |
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
||||||
|
2 |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
61
Лабораторные работы
1. ИЗУЧЕНИЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН
Лабораторная работа 1
Экспериментальное определение функции распределения плотности вероятности результатов измерений
Цель работы: Построение гистограммы результатов измерения и функции распределения плотности вероятности; определение параметров функции распределения.
Приборы и принадлежности: Физический или математический маятник, электрический секундомер.
Методика и техника эксперимента
Величины называются случайными, если в результате опыта вследствие влияния различных случайных причин они могут принимать неодинаковые, но близкие числовые значения. Вероятность случайного события, состоящего, например, в появлении определенной величины а в серии наблюдений, может быть определена как
P a lim |
n |
, |
(1) |
|
|||
N N |
|
|
|
где n - число наблюдений, при которых появилось событие а; N - полное число наблюдений;
P(a) - вероятность события а.
Из (1) следует, что вероятность P(a) есть число, значение которого лежит в пределах
0 P a 1. |
(2) |
Событие считается достоверным при P(a) = 1; при P(a) = 0 событие невозможно.
Допустим, что произведено большое число N наблюдений величины а. Получен ряд значений а1, а2, ..., аi, ..., аN, которые представляют совокупность случайных величин. Результат измерения можно представить
62

графически в виде диаграммы, которая показывает, как часто получаются те или иные значения. Такая диаграмма называется гистограммой.
Для построения гистограммы по оси абсцисс откладывают все значения аi в порядке возрастания. Далее весь диапазон значений разбивается на одинаковые интервалы а и подсчитывается число значений величины а, попавших в каждый интервал. Величина интервала определяется из выражения
a |
amax amin |
, |
(3) |
|
|||
|
k |
|
|
где amax - наибольшее значение измеренной величины, amin - наименьшее значение измеренной величины, k - число интервалов.
Число интервалов берется произвольным, но таким, чтобы в каждом интервале находилось несколько значений аi.
Пусть в первом интервале amin a оказалось n1 значений измерен-
ной величины, во втором – n2 и т.д. Возьмем отношения
nN1 ; nN2 ; nN3 ; ...; nNk ,
которые приближенно равны вероятности того, что величина a принимает значения, соответствующие первому, второму, ..., . к-му интервалу. Разделив эти величины на ширину интервала а, получим
P1 |
n1 |
|
P2 |
n2 |
|
|
Pi |
ni |
|
Pk |
nk |
|
|
N a , |
N a , ..., |
N a , ..., |
N a . |
||||||||||
Величина |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pi |
|
ni |
|
|
|
|
(4) |
||
|
|
|
|
N |
a |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
представляет вероятность, приходящуюся на единичный интервал или плотность вероятности, 1 i k . Плотность вероятности не одинакова для разных интервалов, т.е. изменяется с изменением значения a.
63
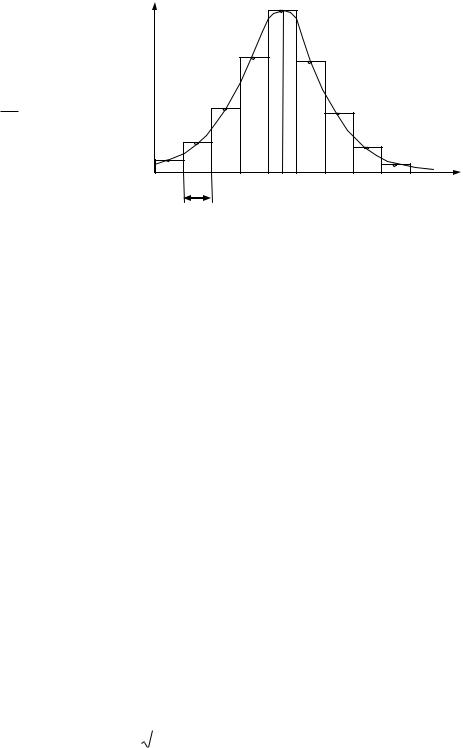
Площадь каждого пря- Pi(a) f(a) |
|
|
||
моугольника гистограммы с |
|
|
|
|
учетом (4) равна |
|
|
|
|
wi Pi a |
ni |
|
|
|
N |
|
|
|
|
|
|
|
|
|
и представляет вероятность |
|
|
|
|
того, что величина а лежит в |
|
a |
a |
|
пределах от ai до ai a . |
|
|||
a |
|
|
||
При увеличении числа интервалов k до бесконечности величина a стре- |
||||
мится к нулю, что возможно только при |
N , т.е. |
при бесконечном |
||
числе измерений. В этом случае ступенчатая фигура перейдет в плавную |
||||
кривую f(а), изображенную на рисунке пунктирной линией. Эта функция |
||||
называется функцией распределения плотности вероятности величины а. |
||||
Практика измерений показывает, что результаты измерений и их по- |
||||
грешности часто имеют вид так называемого нормального распределе- |
||||
ния или распределения Гаусса. Это связано с тем, что эксперименталь- |
||||
ные данные, полученные при измерении одной и той же величины при |
||||
воспроизводимых условиях, подчиняются следующим закономерностям: |
||||
1)при большом числе наблюдений погрешности равной величины, но разного знака встречаются одинаково часто, т.е. равновероятны;
2)вероятность появления погрешностей уменьшается с ростом величины погрешности, т.е. большие по абсолютной величине погрешности встречаются реже, чем малые.
Аналитическое выражение функции распределения Гаусса имеет вид
|
|
1 |
|
|
|
a a0 |
2 |
|
|
f a |
|
|
e |
2 |
2 |
|
|
||
|
|
|
, |
(5) |
|||||
|
|
|
|
|
|
||||
2 |
|
|
|
||||||
где а0 - абсцисса, соответствующая максимуму функции распределения, истинное значение случайной величины;
2 - дисперсия - параметр распределения, характеризующий ширину кривой.
В теории вероятности показывается, что параметры функции распре-
деления рассчитываются по формулам:
64

|
|
|
|
f(a) |
|
a0 |
a f a da , |
(6) |
|||
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
2 a a0 |
2 f a da . |
|
|||
Площадь, заштрихованная на графике, численно равна вероятности того, что величина а лежит в интервале от а до a da .
Общая площадь по кривыми равна 1:
f a da 1,
1
2
a0 |
a |
a a + da |
|
(7)
что соответствует достоверному событию, т.к. означает, что величина а принимает любое возможное значение. Иначе последнее выражение называется условием нормировки функции распределения.
Поскольку дисперсия характеризует разброс результатов относительно истинного значения, то кривая 2 соответствует большей дисперсии, чем кривая 1.
Результаты любого эксперимента являются случайной величиной, которая описывается какой-либо функцией распределения f(а). Если вид f(а) известен, то по формуле (6) можно найти истинное значение и меру разброса результатов - дисперсию.
В реальных условиях f(а) не известна, а число измерений N конечно. Поэтому находят приближенные параметры функции распределения: вместо истинного значения находят среднее арифметическое результатов измерения
|
|
|
1 |
|
|
|
N |
|
|
|
|
|
a |
|
|
|
ai , |
|
|
(8) |
|||
|
|
|
|
|
|
|
|||||
|
|
|
N i 1 |
|
|
|
|||||
а вместо дисперсии - ее оценку |
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
N |
2 |
|
|||
|
|
|
|
|
|
|
|
||||
H2 |
|
|
|
|
ai |
|
. |
(9) |
|||
|
|
|
a |
||||||||
N 1 |
|||||||||||
|
|
i 1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
65 |
|
|
|
||||

H также называют среднеквадратичным отклонением наблюдений от-
носительно среднего значения.
При проведении серии измерений получается, что сами средние значения, полученные в результате обработки результатов каждого измерения, являются случайными величинами, разброс которых характеризуется
дисперсией для распределения среднего 2. В математической статисти-
ке показано, что
|
|
H |
|
. |
(10) |
|
|
|
|||
|
|||||
|
|
N |
|
||
Следовательно среднеквадратичная погрешность среднего значения рассчитывается по формуле:
|
|
N |
|
|
|||
|
|
ai |
|
2 |
|
||
|
|
a |
|
||||
|
i 1 |
|
|||||
|
. |
(11) |
|||||
N N 1 |
|||||||
Среднее значение a отличается от истинного a0 |
, причем, величину |
||||||
этой погрешности определить невозможно, т.к. не известно истинное значение a0. В этом случае задается значение погрешности а такое, чтобы с вероятностью Р абсолютная величина разности между истинным и средним значениями a0 a не превышала а. Вероятность Р называется до-
верительной вероятностью, а интервал от a a до a a - доверительным интервалом.
В качестве результата измерения принимается доверительный интервал, рассчитанный по среднеквадратичному отклонению для распределения среднего и коэффициенту Стьюдента, учитывающему доверительную вероятность и число измерений:
a tPN . |
(12) |
На лабораторных установках (математический маятник, |
физический |
маятник и т.п.) измеряется время 3-5 колебаний. По указанию преподавателя производится 50 наблюдений. Задачей лабораторной работы является построение гистограммы, функции распределения, а также определение параметров функции распределения.
66

Порядок выполнения работы
1.Произвести 50 измерений времени 3-5 колебаний.
2.Определить наибольшее значение измеренной величины amax и наи-
меньшее значение измеренной величины amin .
3.Разбив весь диапазон значений на 7-8 интервалов, определить ширину интервала а по формуле (3).
4.Записать в таблицу числовые значения границ интервалов.
5.Распределить результаты наблюдений по интервалам.
6.Подсчитать число значений ni из общей совокупности наблюдений аi, попавших в каждый интервал.
7.По формуле (4) рассчитать плотность вероятности в каждом интервале.
8.Построить гистограмму распределения плотности вероятности.
9.Провести пунктиром сглаженную кривую функции распределения f(а).
10.По формуле (8) вычислить среднеарифметическое значение a .
11.По формуле (9) рассчитать среднеквадратичное отклонение наблюде-
ний Н.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
||
|
|
|
|
|
|
|
распределения Гаусса f a |
1 |
|
|
2 2H . |
|||||||||
12. Построить |
функцию |
|
e |
|
||||||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
2 H |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для |
этого |
отклонениям |
от среднего |
a a a |
задать |
значения: |
||||||||||||||
a1 |
0, a2 |
H , |
a3 |
2 H , a3 |
3 H . Следует учесть, что |
|||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
при |
a1 0 |
f a |
|
|
h и соответствует высоте эксперимен- |
|||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
2 H |
|
|
|
|
|
|
|
|
|
|
|||
тальной кривой. В этом случае функция распределения приводится к
|
|
|
|
|
a2 |
||
|
|
|
|
|
i |
|
|
виду: |
f a |
i |
h e |
2 2H . |
|||
|
|||||||
|
|
|
|
|
|
||
13.Сравнить построенную функцию распределения с экспериментальной.
14.Сделать вывод о проделанной работе.
67

|
|
|
Интервалы |
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
… |
6 |
7 |
|
|
|
|
|
|
|
Левая |
amin |
amin a |
amin 2 a |
… |
amin 5 a |
amin 6 a |
граница |
|
|
|
|
|
|
|
|
|
|
|
|
|
Правая |
amin a |
amin 2 a |
amin 3 a |
… |
amin 6 a |
amin 7 a |
граница |
|
|
|
|
|
|
|
|
|
|
|
|
|
Значе- |
|
|
|
|
|
|
ния |
|
|
|
|
|
|
ni
Рi
Контрольные вопросы
1.Какие величины называются случайными?.
2.Что называют вероятностью случайной величины? Поясните практический смысл вероятности.
3.Дайте определение плотности вероятности, функции распределения.
4.Какие предположения лежат в основе распределения Гаусса?
5.Поясните смысл функции распределения f a и параметра H . Как от этого параметра зависит форма кривой Гаусса?
6.Что называют доверительной вероятностью и доверительным интервалом?
7.Поясните смысл параметра . Как этот параметр связан с H ?
68

2. ЗАКОНЫ ДИНАМИКИ
Лабораторная работа 2-1
Проверка основного закона динамики вращательного движения
Цель работы: Изучение законов динамики поступательного и вращательного движения.
Приборы и принадлежности: Маятник Обербека, набор грузов, штангенциркуль, электрический секундомер, метрическая шкала.
Методика и техника эксперимента
Маятник Обербека представляет собой крестовину, которая с малым трением может вращаться вокруг горизонтальной оси. С крестовиной скреплен вал диаметром d , на который можно наматывать нить, перекинутую через неподвижный блок. К свободному концу нити прикреплен груз массой m . На стержнях крестовины можно укреплять грузы массой m0 . При отсутствии грузов на стержнях маятник Обербека имеет собственный момент инерции J0. Если систему предоставить самой себе, то груз m будет ускоренно опускаться, приводя в движение маятник. Высоту опускания груза h отсчитывают по вертикальной сантиметровой шкале, укрепленной на стене, а время, в течение которого груз проходит расстояние h,
измеряют электрическим секундомером. |
|
|
|
|
|
Применим законы |
динамики и |
J |
m0 |
|
|
кинематические уравнения для опи- |
|
T |
|
|
|
сания движения системы тел на экс- |
|
|
|
||
|
|
|
|
||
периментальной установке.. |
|
|
T |
||
На груз, движущийся поступа- |
|
|
|
|
|
тельно, действуют сила тяжести mg |
|
|
|
|
|
|
|
|
|
||
и сила натяжения нити T. По второ- |
|
|
|
a |
|
|
|
|
|
|
|
му закону Ньютона |
|
|
mg |
|
|
ma mg T . |
(1) |
|
|
h |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
69

Крестовина совершает вращательное движение под действием момента силы натяжения нити T. Момент силы тяжести, приложенной к маховику, и момент силы реакции оси равны нулю, т.к. линии действия этих сил проходят через ось вращения. Согласно основному закону динамики вращательного движения
J M , |
(2) |
где J - момент инерции маховика, - его угловое ускорение, |
M TR - мо- |
мент силы Т, R d 2 - радиус вала, d - диаметр вала. |
|
Ускорение груза равно ускорению любой точки нити и, соответственно тангенциальному ускорению точек, лежащих на поверхности вала. Оно связано с угловым ускорением соотношением
|
|
|
a a R . |
|||||||
При равноускоренном движении |
|
|
|
|||||||
|
|
|
|
|
h at 2 . |
|
||||
|
|
|
|
|
|
|
|
2 |
|
|
Из (4) a 2h , из (3) |
|
a |
|
|
2h |
. |
|
|
|
|
|
|
|
|
|
|
|||||
t 2 |
|
R |
t |
2 d |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4h |
. |
|
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
t 2d |
|
|
Из (1) T m g a . |
M T d |
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
||
|
|
M m |
d |
|
2h |
|||||
|
|
|
|
g |
. |
|||||
|
|
|
|
|
|
2 |
|
t 2 |
||
(3)
(4)
(5)
(6)
В первой части работы на маховике дополнительных грузов нет , его момент инерции постоянен и равен J0. Меняя грузы, движущиеся поступательно, мы тем самым изменяет момент силы Т, соответственно, изменяется и угловое ускорение маховика. Запишем уравнение динамики вращательного движения для разных опытов.
J0 1 M1
J0 2 M2
Из этих уравнений следует, что
70
