
Механика практикум_уч.пособие
.pdf
|
mv2 |
J |
2 |
|
|
|
mgH |
cm |
|
|
m |
. |
(3) |
2 |
2 |
|
||||
|
|
|
|
|
||
Выразим высоту подъема H через амплитуду a. Обозначим EO R - радиус сферы, по которой движется центр шарика. Из геометрических соображений можно записать:
|
|
|
H 2R H a2 . |
|
|
|
|
||||||||||
При малых амплитудах колебаний H 2R . Тогда |
2RH a2 , |
||||||||||||||||
|
|
|
|
|
|
H |
|
a 2 |
. |
|
|
|
|
(4) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
2R |
|
|
|
|
|
||
Момент инерции шарика относительно центра инерции равен |
|||||||||||||||||
|
|
|
|
|
|
J 2 mr 2 . |
|
|
|
(5) |
|||||||
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
||
Подставим в закон сохранения (3) энергии выражения (4), (1), (2), (5): |
|||||||||||||||||
|
|
|
ma |
2 |
2 2 |
|
|
|
2 |
mr |
2 a 2 |
|
2 2 |
|
|||
|
a 2 |
|
|
|
|
|
|
|
|
|
|
r 2 |
|
|
|
||
mg |
|
|
|
|
T |
|
|
|
5 |
|
|
T |
, |
||||
2R |
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
||||
откуда после алгебраических преобразований получаем: |
|
||||||||||||||||
|
|
|
|
|
g |
28 2 R |
. |
|
|
|
(6) |
||||||
|
|
|
|
|
5T 2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Экспериментально с помощью сферометра измеряется радиус кривизны сферической вогнутой поверхности R’=CO, поэтому
R R r .
Если N - число полных колебаний шарика за t секунд, то период колебаний равен
|
T |
t |
. |
|
|
|
|
|
|
|
|||
|
|
N |
|
|
||
Тогда формула (6) примет вид |
|
|
|
|
|
|
g |
28 2 N 2 R r |
. |
(7) |
|||
5t 2 |
||||||
|
|
|
||||
Для определения радиуса сферической поверхности используется прибор, называемый сферометром. В его описании приведена формула вычисления радиуса сферической поверхности:
111

R |
l 2 |
|
|
h h0 |
|
, |
6 h h |
|
2 |
|
|||
|
0 |
|
|
|
|
|
где l - расстояния между ножками сферометра, h - отсчет по сферометру, помещенному на вогнутую поверхность, h0 - отсчет по сферометру, помещенному на плоскопараллельную пластинку.
При h0 0 R 6l 2h h2 .
Выражение (7) приобретает вид расчетной формулы:
|
14 2 N 2 |
l2 |
|
|
|
g |
5t 2 |
|
|
h d . |
(8) |
|
|||||
|
3h |
|
|
||
где d 2r - диаметр шарика.
Порядок выполнения работы
1.Произвести штангенциркулем однократное измерение диаметра d шарика.
2.Установить сферометр на плоскопараллельную пластинку, предварительно положив на нее лист белой бумаги. Совместить стрелку прибора с нулевым делением шкалы, обеспечивая h0 0 .
3.Получить отпечатки ножек сферометра на бумаге. Измерить линейкой расстояние l между метками.
4.Установить сферометр на металлическую вогнутую поверхность. Снять пятикратно показания сферометра h в разных точках сферы вблизи точки A.
5.Поместить шарик на вогнутую поверхность на расстоянии, примерно равном 10 см по дуге поверхности от положения равновесия. Измерить секундомером время t пяти полных колебаний шарика (N = 5). Опыт повторить 5 раз.
6.Результаты измерений и погрешности измерительных приборов занести в таблицу.
7.Произвести математическую обработку результатов измерений, найти по формуле (8) ускорение свободного падения g и его погрешность g.
112
8.Сравнить полученное значение ускорения с соответствующим значением g для данной географической широты.
Таблица измерений
d, |
d, |
l, |
l, |
h |
h, |
N |
t, |
t, |
мм |
мм |
мм |
мм |
мм |
мм |
|
c |
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольные вопросы
1.Дайте понятие о неинерциальных системах отсчета.
2.Что понимается под силой тяготения, силой тяжести и весом тела?
3.Какое ускорение называется ускорением свободного падения?
4.От каких величин зависит ускорение свободного падения?
5.Объясните зависимость ускорения свободного падения тел от географической широты местности.
6.Выведите расчетную формулу. Какие законы используются при выводе?
Лабораторная работа 4-2
Определение ускорения свободного падения с помощью математического маятника
Цель работы: Определить ускорение свободного падения тел, измеряя период колебаний математического маятника.
Приборы и принадлежности: Математический маятник, секундомер, линейка, штангенциркуль.
Методика и техника эксперимента
Математическим маятником называют колебательную систему, со-
стоящую из невесомой и нерастяжимой нити, на которой подвешена мас-
113
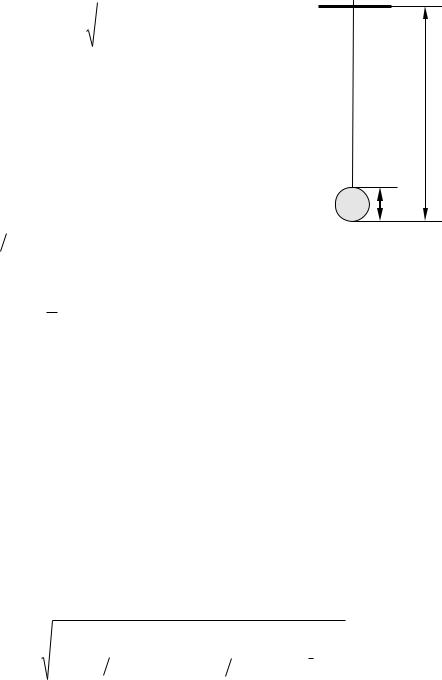
са, сосредоточенная в одной точке. Достаточно хорошим приближением к математическому маятнику служит небольшой тяжёлый шарик, подвешенный на длинной тонкой нерастяжимой нити. Длина маятника l равна расстоянию от точки подвеса до центра тяжести шарика, период колебаний маятника вычисляется по формуле :
T 2 |
|
l |
|
, |
||
g |
||||||
|
|
|
|
|
||
откуда ускорение свободного падения можно выразить |
||||||
как |
|
|
|
|
L |
|
|
|
|
|
|
||
g |
4 2 l |
. |
||||
T 2 |
|
|||||
|
|
|
|
|||
Если измерить расстояние от точки подвеса до
нижнего края шарика L и диаметр шарика d, то длина |
d |
|
|
маятника l L d 2 . |
|
Поскольку период колебаний маятника Т вычисляется по времени t n |
|
полных колебаний T nt , формула для ускорения свободного принимает вид:
|
4 |
2 |
|
d |
2 |
|
|
|
|
L |
n |
|
|
|
|
g |
|
|
|
2 |
|
. |
(1) |
|
|
t 2 |
|
|
|||
|
|
|
|
|
|
|
При работе с математическим маятником имеется возможность изменять длину нити L и время t числа n колебаний. Эту возможность целесообразно использовать для выбора условий выполнения эксперимента с наименьшей погрешностью.
Относительная погрешность косвенного измерения ускорения свободного падения равна
|
g |
|
|
L |
|
2 |
|
|
|
|
|
||
g |
L d |
|
||||
|
|
|
2 |
|||
|
d |
|
2 |
|
|
|
|
|
|
||
2 L d |
2 |
||
2 t 2
(2)t
Из последнего соотношения видно, что увеличение L и t приводит к уменьшению относительной погрешности определения ускорения свободного падения. Поэтому эксперимент нужно выполнять при наибольшей
114
длине нити L, а число колебаний n и соответственно t нужно выбрать также значительными.
Порядок выполнения работы
1.Измерить штангенциркулем диаметр шарика d.
2.Установить максимальную длину нити. Линейкой измерить расстояние L от точки подвеса до нижнего края шарика.
3.Отклонить маятник на угол 15-200 от вертикали. Измерить секундомером время t 10 полных колебаний (n = 10). Измерения повторить 3 раза.
4.Результаты измерений и погрешности измерительных приборов занести в таблицу.
5.Произвести математическую обработку результатов измерений, найти по формуле (1) ускорение свободного падения g и его погрешность g. При расчете погрешности удобно применять метод логарифмирования функции.
6.Сравнить полученное значение ускорения с соответствующим значением g для данной географической широты.
Таблица измерений
d, |
d, |
L, |
L, |
n |
t, |
t, |
мм |
мм |
см |
см |
|
c |
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольные вопросы
1.Дайте понятие о неинерциальных системах отсчета.
2.Что понимается под силой тяготения, силой тяжести и весом тела?
3.Какое ускорение называется ускорением свободного падения?
4.От каких величин зависит ускорение свободного падения?
5.Объясните зависимость ускорения свободного падения тел от географи-
ческой широты местности.
115
6.Что такое математический маятник? Запишите формулу периода математического маятника.
7.Выведите расчетную формулу.
Лабораторная работа 4-3
Определение ускорения свободного падения с помощью физического маятника
Цель работы: вычислить ускорение свободного падения тел, измеряя период колебаний физического маятника, определить параметры физического маятника.
Приборы и принадлежности: физический маятник, математический маятник, секундомер, масштабная линейка.
Методика и техника эксперимента
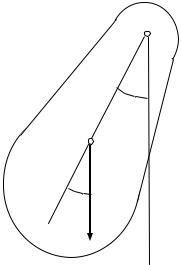
Физическим маятником называется твёрдое тело, способное совершать колебания вокруг неподвижной оси О, не проходящей через центр инерции С. На него действуют сила тяжести mg и сила реакции со стороны
оси . |
|
О |
Поскольку все точки маятника дви- |
|
|
|
|
|
жутся по окружностям, центры которых |
|
|
|
d |
|
расположены на одной оси, его движения |
|
|
|
|
|
является вращательным. При отклонении |
|
|
маятника от положения равновесия на |
С |
|
|
|
|
угол возникает вращательный момент |
|
|
M силы тяжести |
|
|
M mgd sin , |
mg |
|
|
|
|
где m – масса маятника, d - расстояние от оси вращения до центра масс |
||
системы. Знак “минус” обусловлен противоположной направленностью и M. Момент силы реакции оси равен нулю, т.к. линия действия силы проходит через ось вращения.
Применим основной закон динамики вращательного движения:
J M ,
116

в котором d |
|
d 2 |
- угловое ускорение, J - момент инерции маятни- |
|
dt 2 |
||||
dt |
|
|
ка. Преобразуя его к виду
Jd 2 mgd sin dt 2
иучитывая, что при малых углах отклонения маятника sin , получим
дифференциальное уравнение колебательного процесса:
d 2 |
|
mgd |
0 . |
|
dt 2 |
J |
|||
|
|
Как нетрудно увидеть путем прямой подстановки, решение данного уравнения имеет вид:
|
|
|
|
|
|
mgd t 0 |
m sin t 0 , |
||||
m sin |
|
||||
|
J |
|
|
||
т.е. угол изменяется по гармоническому закону, тело совершает гармо-
нические колебания с циклической частотой |
mgd |
и периодом |
|||||
|
|
|
|
|
|
J |
|
|
|
|
|
|
|
|
|
T |
2 2 |
J |
. |
|
(1) |
||
|
|
||||||
|
|
mgd |
|
|
|||
Приведенная длина физического маятника - это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Формула для периода колебаний математического маятника имеет вид:
T 2 |
|
l |
|
. |
(2) |
|
|||||
|
|
g |
|
||
Из сравнения выражений (1) и (2) видно, что приведенная длина физического маятника равна:
l |
J |
. |
(3) |
|
|||
|
md |
|
|
Отложим от точки подвеса О вдоль прямой ОС отрезок ОО , длина которого равна приведенной длине физического маятника l. Точка О называется центром качания. Центр качания можно определить как точку, в
117

которой надо сосредоточить всю массу физического маятника, чтобы период его колебаний остался без изменений.
По теореме Штейнера
J J |
|
md 2 . |
|
|
|
О |
||
c |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Подставив это выражение в формулу (3), полу- |
l |
|
|
|||||
|
|
|
|
|
|
|
d |
|
чим следующее выражение для приведенной |
|
|
||||||
|
|
|
||||||
длины: |
|
|
|
|
|
|
|
|
|
|
|
Jc |
|
|
|
С |
|
l d |
. |
(4) |
|
|
|
|||
|
|
d |
|
|||||
|
|
|
md |
|
|
|
||
Отсюда следует, что, во-первых, l > d, т.е. точка |
|
О |
|
|||||
подвеса О и центр качания О лежат по разные |
|
|
|
|||||
стороны от масс С и, во-вторых, что всем точкам |
|
|
|
|||||
подвеса, одинаково удаленным от центра масс маятника, соответствует одна и та же приведенная длина, а, следовательно, один и тот же период колебаний Т.
Точка подвеса и центр качания являются взаимными или сопряженными точками в следующем смысле. Если маятник подвесить за центр качания О , то его период не изменится и прежняя точка подвеса О сделается новым центром качания. Это положение называется теоремой Гюйгенса.
Пусть О является точкой подвеса. Тогда приведенная длина в соответствии с (4) будет
l d mdJc .
Из рисунка видно, что d l d , а в соответствии с (3) d mdJc . Подста-
вив это значение в предыдущую формулу, получим:
l |
Jc |
|
Jc |
|
d |
Jc |
l , |
|
md |
m |
Jc |
|
md |
||||
|
|
|
|
|
||||
|
|
|
md |
|
|
|
|
|
т.е. приведенная длина, а следовательно, период колебаний физического маятника остались без изменений.
118

Теорема Гюйгенса используется в оборотном маятнике для измере- |
||||||||
ний ускорения свободного падения. Физический оборотный маятник, ис- |
||||||||
пользуемый в данной работе, состоит из металлического стержня, на кото- |
||||||||
ром жестко закреплены две опорные призмы О и О , и три чечевицы. Две |
||||||||
из них находятся на концах стержня, их положение не изменяется при |
||||||||
проведении эксперимента. Третья подвижная чечевица А находится между |
||||||||
опорными призмами. Путем перемещения чечевицы А можно менять рас- |
||||||||
стояние d между точкой подвеса О и центром тяжести С, а также расстоя- |
||||||||
ние d между центром тяжести С и центром качания О . |
|
|||||||
Перемещением |
этой |
чечевицы |
достигают |
|
||||
совпадения периодов колебаний маятника, когда |
О |
|||||||
точками подвеса являются ребра опорных призм |
||||||||
|
||||||||
О и О . Поэтому при совпадении периодов коле- |
|
|||||||
баний расстояние между ними дает приведенную |
|
|||||||
длину физического маятника l. Измеряя период |
|
|||||||
колебаний Т, можно вычислить ускорение g по |
А |
|||||||
|
||||||||
формуле, полученной из (2): |
|
|
|
|||||
|
g |
4 |
2 l |
. |
|
|
||
|
T 2 |
|
|
|||||
|
|
|
|
|
О |
|||
Используя |
формулу |
|
для |
периода |
колебаний |
|||
|
|
|||||||
T t , окончательно находим: |
|
|
||||||
n |
|
|
|
|
|
|
|
|
|
g |
4 2l n2 |
. |
(5) |
|
|||
|
|
t 2 |
|
|
||||
|
|
|
|
|
|
|
||
Из (3) можно выразить момент инерции маятника относительно оси подвеса О: J mdl . Собственный момент инерции маятника относительно оси, проходящей через его центр масс J0, связан с J по теореме Штейнера:
|
|
J J |
0 |
md 2 , |
|
|
|
|
|
|
|
откуда |
|
|
|
|
|
J |
0 |
J md 2 |
mdl md 2 |
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
J0 md l d . |
(6) |
||
|
|
|
119 |
|
|
Задание 1. Определение ускорения свободного падения
Порядок выполнения работы
1.Установить чечевицу в произвольном положении на металлическом стержне. Отклонив маятник на 10 -15° от положения равновесия, привести его в колебательное движение. Секундомером измерить время t1 десяти полных колебаний (n = 10).
2.Повернув маятник, подвесить его на ось противоположным концом и измерить, время t n=10 полных колебаний.
3.Перемещать чечевицу так, чтобы значения t и t сближались. Найденное при совпадении t = t время и есть значение времени в формуле (5). Провести измерение времени 5 раз.
4.Измерить расстояние а от точки подвеса О до подвижной чечевицы А и расстояние а от точки качания О до подвижной чечевицы. Обозначая толщину чечевицы через b, выразим приведенную длину физического маятника как l a a b.
5.Результаты измерений и погрешности измерительных приборов занести в таблицу.
6.Произвести математическую обработку результатов измерений, найти
по формуле g |
4 2 |
a a b n2 |
ускорение свободного падения g, а |
|
t 2 |
||
|
|
|
также его погрешность g.
7.Сравнить полученное значение g с соответствующим для данной географической широты.
Таблица измерений
n |
t, с |
t , с |
t, с |
а, см |
а , см |
b, мм |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
120
