
Механика практикум_уч.пособие
.pdf
|
|
|
|
|
h at 2 |
|
(4) |
|
|||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
Разрешим систему уравнений (1) - (4) относительно момента инерции. |
|||||||||||||
Из (3)выразим |
a |
, |
из (1) T m g a и подставим в (2): |
|
|
|
|||||||
|
|
|
|
||||||||||
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J |
a |
m g a R , |
|
|
|
|||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 g |
|
|
откуда момент инерции колеса определится выражением: J mR |
|
|
1 |
||||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
Учитывая, что согласно (4) a 2h , а |
R d 2 , окончательно получим: |
||||||||||||
|
|
|
|
t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
J md |
2 |
|
gt |
2 |
|
|
|
|
||
|
|
|
|
|
|
1 |
(5) |
|
|||||
|
|
|
|
|
|
|
|||||||
|
|
|
4 |
|
|
2h |
|
|
|
|
|||
Порядок выполнения работы
1.Положить груз на платформочку, прикрепленную к шнуру, найти суммарную массу m платформочки и груза.
2.Вращая колесо, поднять груз на такую высоту, чтобы край платформочки совпадал с нулевым делением вертикальной шкалы.
3.Отпустив колесо, измерить время t, в течение которого груз опустится на высоту h.
4.Провести пять опытов, не изменяя массу груза и высоту падения.
Таблица измерений
|
m, |
d, |
dси |
t, |
tси, |
h, |
hси, |
g |
|
г |
мм |
мм |
с |
с |
см |
см |
м/с2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. С помощью штангенциркуля провести однократное измерение диаметра вала.
81
6.Результаты измерений и погрешности измерительных приборов занести в таблицу.
7.Произвести математическую обработку результатов измерений, найти момент инерции колеса J и его погрешность J.
Контрольные вопросы
1.Виды движения твердого тела. Какое движение называется поступательным? вращательным?
2.Какие величины являются мерой инертности при поступательном и вращательном движении? Дайте их определение.
3.Сформулируйте теорему Штейнера.
4.Какие физические величины являются мерой воздействия при поступательном и вращательном движении?
5.Сформулируйте законы динамики поступательного и вращательного движения.
6.Ускорение при поступательном и вращательном движении. Угловое ускорение. Связь между линейными и угловыми кинематическими величинами.
7.Выведите расчетную формулу.
Лабораторная работа 2-3 Определение момента инерции маятника Максвелла
Цель работы: изучение законов динамики поступательного и вращательного движения, экспериментальное определение момента инерции маятника Максвелла.
Приборы и принадлежности: маятник Максвелла, сменные кольца, электрический миллисекундомер, миллиметровая шкала.
Методика и техника эксперимента
Маятник Максвелла представляет собой массивный диск или колесо, к концам оси которого прикреплены два шнура; за концы этих шнуров маятник подвешивают к опоре.
82
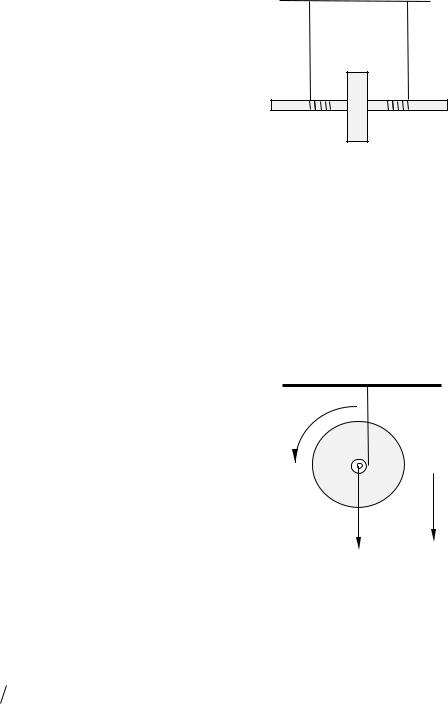
Если шнуры намотать на ось и затем отпустить маятник, то под действием силы тяжести шнуры будут разматываться и маятник будет опускаться с ускорением а. Опустившись в крайнее нижнее положение, при котором шнуры полностью размотаны, колесо будет по инерции вращаться в том же направлении, шнуры намотаются на ось, вследствие чего маятник поднимется.
Применим законы динамики и кинематические уравнения для описания движения маятника Максвелла. Маятник участвует в двух движениях: прямолинейном движении центра масс с ускорением а и вращательном движении вокруг оси, проходящей через центр масс, с угловым ускорением . На маятник действуют сила тяжести mg и сила натяжения нити T.
Согласно уравнению движения центра масс, совпадающему по форме с вторым законом Ньютона, имеем:
ma mg T . |
(1) |
Вращательное движение маятник |
совершает |
под действием момента силы натяжения нити T. Момент силы тяжести, приложенной к маховику, равен нулю, т.к. линия действия этой силы проходят через ось вращения. Применим основной закон динамики вращательного движения:
T 
a
mg
J M , |
(2) |
где J - момент инерции маятника, - его угловое ускорение, |
M TR - мо- |
мент силы Т, R d 2 - радиус вала, d - диаметр вала. |
|
Ускорение маятника связано с угловым ускорением соотношением |
|
a R . |
(3) |
При равноускоренном движении |
|
h at 2 |
(4) |
2 |
|
Разрешим систему уравнений (1) - (4) относительно момента инерции.
83
Из (3) выразим Ra , из (1) T m g a и подставим в (2):
J |
a |
m g a R , |
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||||
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
g |
|
|
откуда момент инерции колеса определится выражением: |
J mR |
|
|
|
1 |
|||||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
Учитывая, что согласно (4) a 2h , а |
R d 2 , окончательно получим: |
|||||||||||
|
t 2 |
|
|
|
|
|
|
|
|
|
|
|
J md |
2 |
|
gt |
2 |
|
|
|
|
|
|
||
|
|
|
1 |
|
(5) |
|
||||||
|
|
|
|
|
||||||||
4 |
|
|
2h |
|
|
|
|
|
|
|||
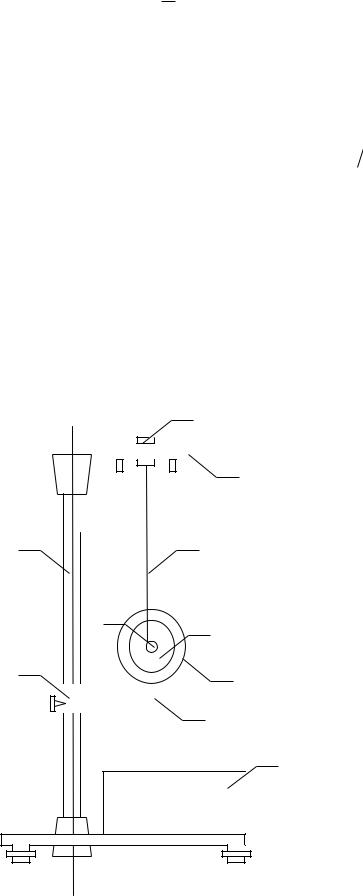
Установка, используемая в данной работе, состоит из вертикальной стойки, где крепятся два кронштейна: верхний 1 и нижний 2. Верхний кронштейн снабжен электромагнитом и устройством 3 для крепления бифилярного подвеса 4. Маятник представляет собой диск 5, закрепленный на оси 6, подвешенной на бифилярном подвесе.
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
На диск 5 крепятся сменные |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кольца 7. Маятник со сменными |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кольцами фиксируется в верхнем ис- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ходном положении с помощью элек- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тромагнита. На вертикальной стойке |
8 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
8 нанесена миллиметровая шкала, |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
имеющая пределы 0 - 420 мм. Фото- |
|
6 |
|
|
|
5 |
датчик 9 выдает электрические сиг- |
||||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
налы на миллисекундомер 10 с циф- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
ровой индикацией времени. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Порядок выполнения работы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Подготовить маятник к работе. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10Для этого установить с помощью устройства 3 необходимую длину
бифилярного подвеса таким образом, чтобы край среза сменного кольца маятника находился на 4-5
84
мм ниже оптической оси фотодатчика 9.
При этом ось маятника должна занять горизонтальное положение.
2.Подключить фотодатчик к разъему ВХОД на миллисекундомере.
3.Подготовить миллисекундомер к работе:
-включить в сеть шнур питания миллисекундомера;
-нажать кнопку СЕТЬ на лицевой панели миллисекундомера, при этом должны загореться цифровые индикаторы и лампочка фотоэлектрического датчика;
-нажать кнопку СБРОС на передней панели миллисекундомера.
4.Вращая маятник, зафиксировать его в верхнем положении с помощью электромагнита. Необходимо следить за тем, чтобы нить наматывалась на ось виток к витку.
5.Нажать кнопку ПУСК на миллисекундомере. При этом электромагнит и маятник обесточиваются, маятник приходит в движение, начинается отсчет времени. В момент пересечения маятником оптической оси фотодатчика счет времени прекращается.
6.Определить время t движения маятника по миллисекундомеру.
7.По миллиметровой шкале, пользуясь указателем кронштейна 2, определить пройденное маятником расстояние h.
8.Провести пять опытов с одним и тем же кольцом, не изменяя высоту падения.
Таблица измерений
m, |
d, |
dси. |
t, |
tси, |
h, |
hси, |
g |
г |
мм |
мм |
с |
с |
см |
см |
м/с2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
85
9.С помощью штангенциркуля провести однократное измерение диаметра d оси.
10.Результаты измерений и погрешности измерительных приборов занести в таблицу.
11.Произвести математическую обработку результатов измерений, найти момент инерции маятника J и его погрешность J.
Контрольные вопросы
1.Виды движения твердого тела. Какое движение называется поступательным? вращательным?
2.Какие величины являются мерой инертности при поступательном и вращательном движении? Дайте их определение.
3.Сформулируйте теорему Штейнера.
4.Какие физические величины являются мерой воздействия при поступательном и вращательном движении?
5.Сформулируйте законы динамики поступательного и вращательного движения.
6.Ускорение при поступательном и вращательном движении. Угловое ускорение. Связь между линейными и угловыми кинематическими величинами.
7.Выведите расчетную формулу.
86
|
|
3. ЗАКОНЫ СОХРАНЕНИЯ |
|
|
|
|
Лабораторная работа 3-1 |
|
|
Определение момента инерции твердого тела |
||||
|
|
методом колебаний |
|
|
Цель работы: Изучение закона сохранения энергии, экспериментальное |
||||
определение момента инерции колеса. |
|
|||
Приборы и принадлежности: Колесо на горизонтальной оси, вспомога- |
||||
|
|
тельный груз, штангенциркуль, линейка, |
||
|
|
электрический секундомер. |
||
|
|
Методика и техника эксперимента |
||
Целью работы является определение момента инерции колеса J. За- |
||||
крепленное на горизонтальной оси, колесо находится в безразличном рав- |
||||
новесии. Если к ободу махового колеса прикрепить с помощью винта ка- |
||||
кое-либо тело небольших размеров, то безразличное равновесие системы |
||||
заменяется устойчивым, т.е. колесо, выведенное из состояния равновесия, |
||||
совершает колебания. |
|
|
||
Прикрепим к колесу шарик радиуса r, диаметром d и массой m. Ради- |
||||
ус колеса равен R, диаметр D. |
|
|
||
Отклоним колесо от положение |
|
|
||
равновесия на малый угол 0. Будем |
|
|
||
считать, что трение в оси вращения |
|
|
||
и о воздух пренебрежимо мало. Ко- |
R |
О |
||
лесо станет совершать колебания по |
0 |
|
||
гармоническому закону с амплиту- |
|
|||
I |
|
|||
дой 0 и периодом Т. Уравнение |
a |
|||
|
|
|||
движения будет иметь вид: |
h |
|
||
|
|
cos 2 t . |
|
r |
0 |
|
II |
||
|
T |
|
||
|
|
|
|
|
Угловая скорость вращательного движения колеса тоже будет изменяться |
||||
по гармоническому закону: |
|
|
||
87
|
d |
|
|
2 sin 2 t |
|
|
0 |
||||
|
dt |
T |
T |
||
|
|
||||
Она принимает максимальное значение, равное
|
m |
|
0 |
2 |
, |
(1) |
|
|
T |
|
|
||
|
|
|
|
|
|
в те моменты времени, когда шарик находится в нижней точке траектории (здесь учитывается тот факт, что синус по модулю не может превышать единицы).
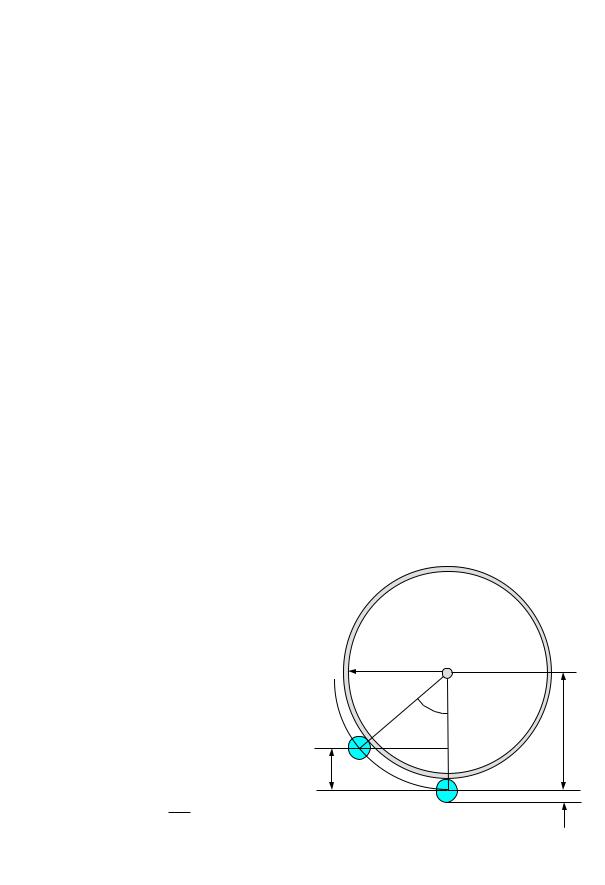
Рассмотрим два состояния системы тел “колесо + шарик”, изображенные на рисунке и применим закон сохранения энергии. В крайнем состоянии I система обладает запасом потенциальной энергии вследствие того, что шарик поднят на высоту h:
WI Wпот mgh .
В состоянии II эта система тел обладает кинетической энергией вращательного движения:
W W |
|
|
|
J J |
|
|
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
ш |
|
|
m , |
|
||||||||
I1 |
|
|
кин |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где J и Jш - моменты инерции колеса и шарика относительно оси вращения |
|||||||||||||||||||||
О. По закону сохранения энергии WI |
WI1 имеем: |
|
|||||||||||||||||||
|
|
|
|
|
|
J J |
ш |
|
2 |
|
|
|
|
||||||||
|
mgh |
|
|
|
|
|
|
|
|
|
m |
|
|
|
|||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
или с учетом (1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mgh |
J Jш |
2 |
|
|
|
2 |
(2) |
||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
T |
|
|
|
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||||
Отсюда выразим момент инерции колеса: |
|
|
|
|
|
|
|
|
|
||||||||||||
|
J |
|
|
2mgh |
|
|
|
Jш . |
|
(3) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
|
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Шарик движется по окружности радиуса |
a R r D d |
. Его мо- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
мент инерции найдем по теореме Штейнера:
88

|
|
|
|
|
2 |
|
m D d |
2 |
|
|
|
2 |
D d |
2 |
|
|
J |
|
2 mr 2 |
ma 2 |
md |
|
|
|
m d |
|
|
|
. (4) |
||||
|
|
|
|
|
|
|||||||||||
|
ш |
5 |
|
10 |
4 |
|
2 |
|
5 |
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|||||||||
Выразим высоту h через угол отклонения колеса 0. Из рисунка вид-
но, что cos |
0 |
a h , откуда h a 1 cos |
0 |
. Учитывая известное триго- |
||||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нометрическое соотношение 1 cos |
0 |
2 sin2 0 и условие малости угла |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отклонения 0, при котором sin |
|
0 |
|
|
0 |
|
, получаем: |
|
|
|
|
|
|
|||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h 2a sin2 |
|
0 |
a |
|
0 |
2 |
|
|
D d |
0 |
2 |
. |
|
(5) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2 |
2 |
|
|
|
4 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Подставив (4) и (5) в (3), получим: J m |
gT 2 D d |
2d |
2 |
D d 2 |
|
|||||||||||||||||||
|
|
|
|
|
|
. |
||||||||||||||||||
|
|
2 2 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
5 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если t - время полных n колебаний, то период равен T nt . С учетом по-
следнего выражения расчетная формула для момента инерции колеса принимает вид:
J m |
gt 2 |
D d |
2d |
2 |
D d 2 |
|
|
|
|
|
|
|
. |
(6) |
|||
2 2n2 |
|
|||||||
4 |
|
5 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Порядок выполнения работы
1.Вывести систему из положения равновесия, придав ей угловое смещение 30-40 , и предоставить ей возможность свободно колебаться.
2.Измерить по секундомеру время n полных колебаний t. Известно, что по мере увеличения n погрешность измерений уменьшается. Однако при большом n колебания становятся затухающими, поэтому целесообразно выбрать n = 5-10 колебаний. Опыт повторить 5 раз.
3.Произвести штангенциркулем однократное измерение диаметра d шарика.
4.Произвести линейкой однократное измерение диаметра D колеса.
5.Результаты измерений и погрешности измерительных приборов занести в таблицу.
89
6.Произвести математическую обработку результатов измерений, найти по формуле (6) момент инерции колеса J и его погрешность J.
Таблица измерений
№ |
t, |
n |
tси, |
D, |
Dси, |
d, |
dси, |
m, |
пп |
с |
|
с |
см |
мм |
мм |
мм |
г |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольные вопросы |
|
|
|
||
1.Дайте определение момента инерции материальной точки и твердого тела. В каких единицах он измеряется?
2.Сформулируйте теорему Штейнера.
3.Механическая энергия и ее виды. Кинетическая энергия при поступательном и вращательном движении.
4.Сформулируйте законы изменения и сохранения .энергии в механике.
5.Запишите уравнение свободных незатухающих колебаний. Дайте определения основных характеристик этого движения (амплитуды, фазы, периода, частоты).
6.Получите зависимость скорости колебательного движения от времени. Чему равно максимальное значение скорости?
7.Выведите расчетную формулу.
Лабораторная работа 3-2
Определение скорости полета пули с помощью баллистического маятника
Цель работы: Изучение законов сохранения энергии и импульса, экспериментальное определение скорости полета пули.
90
