Вопросы для допуска к выполнению лабораторной работы

1. Дайте понятие поляризации диэлектрика.

2. Что такое вектор поляризации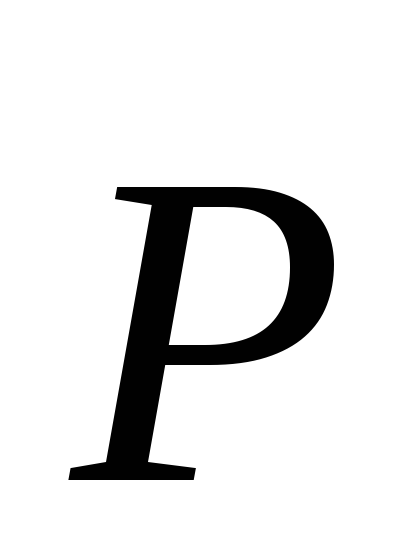? Вектор электрического смещения? Диэлектрическая проницаемость ε и диэлектрическая восприимчивость?

3. Что такое спонтанная поляризация?

4. Опишите свойства сегнетоэлектриков.

5. Что такое гистерезис? Проиллюстрируйте свой ответ.

Контрольные вопросы

1. В чем заключается поляризация диэлектриков? Какая величина является количественной характеристикой поляризации? Как эта величина связана с напряженностью электрического поля в диэлектрике?

2. Опишите различные типы поляризации: электронного смещения, ионного смещения, ориентационную, спонтанную.

3. Опишите основные свойства сегнетоэлектриков.

4. Нарисуйте принципиальную электрическую схему для получения петли гистерезиса и объясните ее работу.

5. Получите формулу, по которой в работе определяется диэлектрическая проницаемость сегнетоэлектрика.

Используемая литература

[1] §§ 15.1 – 15.5;

[2] §§ 12.1 – 12.5;

[3] §§ 2.19, 5.66 – 5.68;

[4] §§ 2.8; 2.9.

Лабораторная работа 2-03

Определение емкости конденсаторов при помощи мостиковой схемы

Цель ра­бо­ты: оп­ре­де­ле­ние ём­ко­сти кон­ден­са­то­ров при раз­лич­ных их соедине­ни­ях с по­мо­щью мос­та пе­ре­мен­но­го то­ка. Оз­на­ком­ле­ние с ра­бо­той мос­та Со­тти.

Теоретическое введение

Рассмотрим уединённый заряженный проводник. При равновесном распределении заряда потенциал любой его точки одинаков и прямо пропорционален заряду:, а коэффициент пропорциональности – это ёмкость проводника:

. (3.1)

Электроемкость уединенного проводника показывает, какой заряд нужно сообщить данному проводнику, чтобы его потенциал изменился на единицу. Еди­ни­цей элек­тро­ем­ко­сти в сис­те­ме СИ яв­ля­ет­ся 1 фа­ра­д – это электроем­кость та­ко­го про­вод­ни­ка, по­тен­ци­ал ко­то­ро­го при со­об­щении за­ря­да в 1 ку­лон из­ме­ня­ет­ся на 1 вольт:

.

Элек­тро­ем­кость уе­ди­нен­но­го про­вод­ни­ка – это од­на из его ха­рак­те­ри­стик, ко­то­рая по­ка­зы­ва­ет, ка­кой за­ряд нуж­но со­об­щить данно­му про­вод­ни­ку, чтобы его по­тен­ци­ал из­ме­нил­ся на еди­ни­цу, и опре­де­ля­ет­ся по фор­му­ле:

, (3.1а)

где C – ем­кость про­вод­ни­ка; – измерение потенциала проводника при со­об­ще­нии ему за­ря­да . Элек­тро­ем­кость про­вод­ни­ка за­ви­сит от его раз­ме­ров, фор­мы, нали­чия по со­сед­ст­ву дру­гих про­вод­ни­ков и от ди­элек­три­че­ской прони­цае­мо­сти сре­ды.

Кон­ден­са­то­ром на­зы­ва­ет­ся со­во­куп­ность двух лю­бых проводников с оди­на­ко­вы­ми по аб­со­лют­но­му зна­че­нию, но про­ти­во­по­лож­ны­ми по зна­ку за­ря­да­ми. Напряжение на конденсаторе U (разность потенциалов обкладок) тем больше, чем больше заряд конденсатора:

.

Коэффициентом пропорциональности между ними является ёмкость конденсатора C:

. (3.2)

Ём­кость кон­ден­са­то­ра оп­ре­де­ля­ет­ся от­но­ше­ни­ем за­ря­да на од­ной из его об­кла­док к раз­но­сти по­тен­циа­лов (напряжению) ме­ж­ду об­клад­ка­ми:

. (3.2а)

Ёмкость конденсатора зависит от формы и размера обкладок, их взаимного расположения и электрических свойств окружающей среды. В боль­шин­ст­ве слу­ча­ев фор­ма об­кла­док кон­ден­са­то­ра и их вза­им­ное рас­по­ло­же­ние под­би­ра­ют та­ким об­ра­зом, что­бы внеш­ние по­ля су­ществен­но не влия­ли на элек­три­че­ское по­ле ме­ж­ду ни­ми и си­ло­вые линии, на­чи­наю­щие­ся на од­ной из об­кла­док, обя­за­тель­но за­кан­чи­ва­лись на дру­гой. Бла­го­да­ря это­му все­гда обес­пе­чи­ва­ет­ся ра­вен­ст­во аб­солют­ных зна­че­ний за­ря­дов на об­клад­ках.

К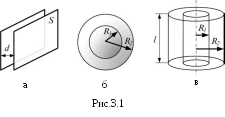про­стей­шим ти­пам кон­ден­са­то­ров от­но­сят­ся пло­ские, сфе­ри­че­ские и ци­лин­д­ри­че­ские. Ёмкость приведенных на рисунке 3.1 конденсаторов может быть рассчитана по формулам:

плоский конденсатор (рис.3.1,а):

; (3.3)

сферический конденсатор (рис.3.1,б):

; (3.4)

цилиндрический конденсатор (рис.3.1,в):

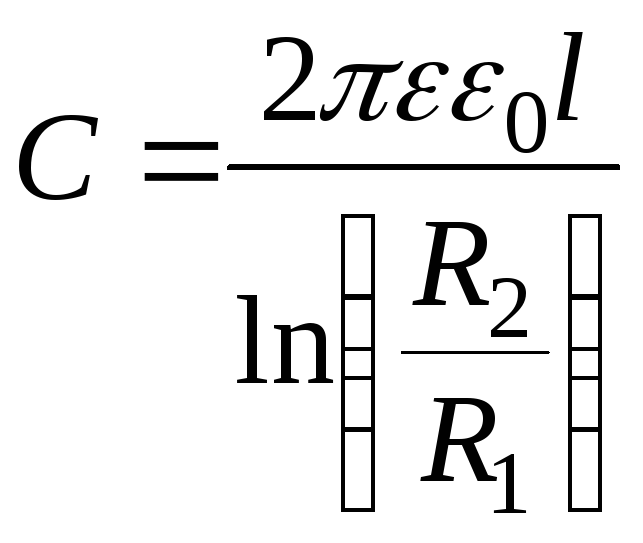. (3.5)

Докажем формулы (3.3-3.5):

Для вычисления разности потенциалов на обкладках конденсатора воспользуемся формулой связи напряженности электростатического поля и потенциала:

;

.

Здесь и– потенциалы одной и второй обкладки конденсатора соответственно. То есть:

. (3.6)

В плоском конденсатореполе однородно, поэтому. Напряжённость поля плоского конденсатора равна, где– поверхностная плотность заряда обкладок. Тогда

.

Для вычисления напряжённости поля сферического конденсатора используем теорему Остроградского-Гаусса (3.7), согласно которойпоток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов, охваченных поверхностью, деленной на εε₀:

. (3.7)

Здесь ,,– единичный вектор нормали к гауссовой поверхности, показанной на рис.3.2 пунктиром, α – угол между нормалью и вектором напряжённости. Радиус гауссовой поверхности равенr, причёмR₁<r<R₂. Из-за симметрии напряженность поля в любой точке гауссовой поверхности одинакова и совпадает по направлению с нормалью к поверхности в данной точке, тогда,, и

.

Здесь учтено, что – площадь сферы. Суммарный заряд, охваченный Гауссовой поверхностью, – это заряд внутренней обкладкиq. Тогда

. (3.8)

Из (3.6):

.

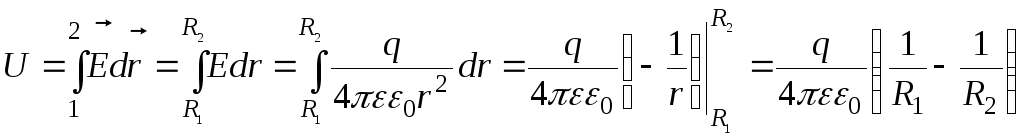Теперь можно рассчитать ёмкость сферического конденсатора:

.

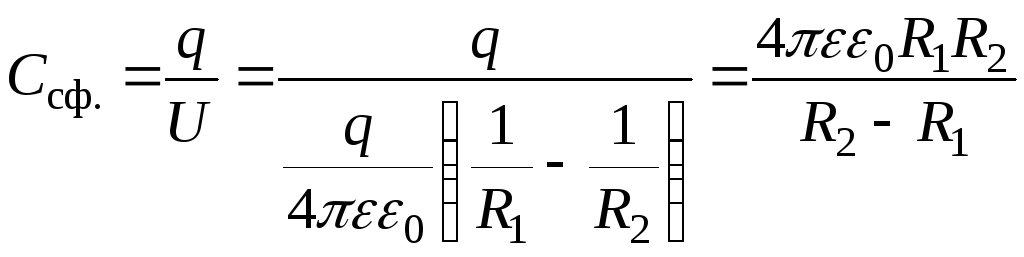Аналогично для цилиндрического конденсатора (рис.3.3) по теореме Гаусса:

.

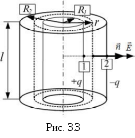
В качестве Гауссовой поверхности здесь взяли цилиндр, коаксиальный обкладкам цилиндрического конденсатора, радиусом r(r₁<r<r₂) и длинойl. Здесь– площадь боковой поверхности этого цилиндра. Поток вектора напряжённости через основания цилиндра учитывать не надо; он равен нулю, так как напряжённость поля перпендикулярна нормали к основанию:.

Далее, из (3.6):

.

По определению ёмкости

.

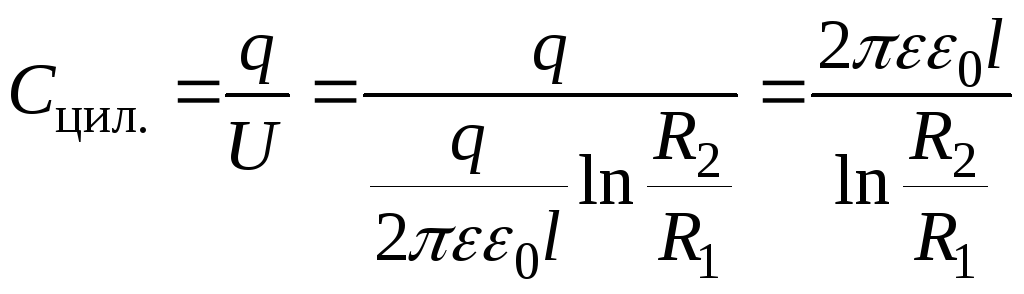К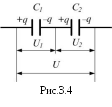онденсаторы характеризуются не только их элек­три­че­ской ём­ко­стью, но так­же и на­пря­же­ни­ем про­боя – та­кой ми­ни­маль­ной раз­но­стью по­тен­циа­лов обкла­док, при ко­то­рой про­ис­хо­дит элек­три­че­ский раз­ряд че­рез слой ди­элек­три­ка в кон­ден­са­то­ре.

По­сле­до­ва­тель­но кон­ден­са­то­ры со­еди­ня­ют в том слу­чае, ко­гда их нужно вклю­чить в цепь с на­пря­же­ни­ем вы­ше то­го, на ко­то­рое рас­счи­тан от­дель­ный кон­ден­са­тор. При последовательном соединении заряды конденсаторов оказываются одинаковыми, а напряжения складываются (рис.3.4):

,

.

Здесь n– общее число соединённых последовательно конденсаторов,– напряжение наi-том конденсаторе. Из определения ёмкости

, ,

тогда после преобразований:

. (3.9)

Ве­ли­чи­на, об­рат­ная ём­ко­сти ба­та­реи, рав­на сум­ме об­ратных ве­ли­чин ёмкостей от­дель­ных кон­ден­са­то­ров.

При по­сле­до­ва­тель­ном со­еди­не­нии за­ря­ды на кон­ден­са­то­рах оди­на­ко­вы, на­пря­же­ние на них рас­пре­де­ля­ет­ся в за­ви­си­мо­сти от их ем­ко­стей, что умень­ша­ет воз­мож­ность про­боя кон­ден­са­то­ра.

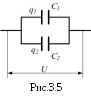
В тех слу­ча­ях, ко­гда ём­ко­сти од­но­го кон­ден­са­то­ра ока­зы­ва­ет­ся не­дос­та­точ­но, кон­ден­са­то­ры со­еди­ня­ют па­рал­лель­но (рис.3.5). При этом напряжение на них одинаково и равно общему:

,

а заряды складываются:

.

Из определения ёмкости.

,

.

Тогда

,

. (3.10)

Ём­кость ба­та­реи кон­ден­са­то­ров рав­на сум­ме ём­ко­стей от­дель­ных кон­ден­са­то­ров.