Вопросы для допуска к выполнению лабораторной работы

1. Какие токи называются квазистационарными?

2. Нарисуйте схему зарядки конденсатора; напишите для неё второе правило Кирхгофа.

3. Нарисуйте график зависимости напряжения на конденсаторе от времени при его зарядке.

4. То же самое (см. пп.2 и 3) для процесса разрядки конденсатора. Как изменится график, если увеличить сопротивление резистора, через который происходит разрядка конденсатора? Если уменьшить ёмкость?

5. Что называется временем релаксации (постоянной времени RC-цепочки)?

6. Что такое «половинное время»? Как связано со временем релаксации?

7. Опишите способы экспериментального определения постоянной времени RC-цепочки τ.

Контрольные вопросы

1. Что такое «релаксация заряда»?

2. Как определяется характеристическое время релаксации τ?

3. Опишите блок-схему установки.

4. Как зависит время заряда и разряда конденсатора от элементов цепи R₁, R₂, C?

5. Какова зависимость напряжения на конденсаторе Uи тока в цепиIот времени, т.е.U(t) иI(t), в процессе заряда и разряда конденсатора? Нарисуйте графики.

6. Нарисуйте схему зарядки конденсатора; с помощью второго правила Кирхгофа получите дифференциальное уравнение для заряда q, решите его. Нарисуйте график полученной функцииq(t) – формула (6.5).

7. То же самое (п.6) для разрядки конденсатора – формула (6.9).

Используемая литература

[2] §§ 13.8;

[3] §§ 8.6;

[4] § 127.

Лабораторная работа 2-07

Изучение релаксационных колебаний (ФПЭ-12)

Цель работы:снятие вольтамперной характеристики газонаполненной лампы и изучение релаксационных колебаний.

Теоретическое введение

Релаксационные колебания – незатухающие негармонические колебания нелинейных систем, для которых характерно накопление и сбрасывание энергии (relaxation – ослабление). Для получения релаксационных колебаний часто используют систему «газонаполненная лампа-конденсатор» (рис.7.1).

Рассмотрим идеализированную вольтамперную характеристику газонаполненной лампы (рис.7.2).

Вобычных условиях газы ведут себя как изоляторы, поскольку состоят из нейтральных молекул. Концентрация в них ионов, образующихся под действием космических лучей, крайне невелика, так что сопротивление лампы практически бесконечно, и ток в лампе отсутствует.

Если увеличивать разность потенциалов на электродах лампы, то лампа “загорается”. Процессы, приводящие к резкому увеличению концентрации свободных носителей тока (ионов обоего знака и свободных электронов), разнообразны. Это ударная ионизация, фотоионизация, фотоэффект, вторичная электронная эмиссия и, главное, выбивание электронов с поверхности катода положительными ионами, ускоренными в достаточно сильном электрическом поле. Повышая напряжение на электродах, можно возбудить все эти процессы и осуществить переход от несамостоятельного разряда к самостоятельному. Этот переход называется электрическим пробоем газа, а соответствующее напряжение – напряжением зажигания (U_з). Оно зависит от химической природы газа, материала катода, формы электродов и расстояния между ними, давления газа и наличия в нем примесей.

При значении U=U_з скачком устанавливается значение тока, равное I_з. При дальнейшем возрастании напряжения ток растет по закону, близкому к линейному. Если затем уменьшать напряжение на “горящей” лампе, то при напряжении, равном U_з, лампа ещё не гаснет. Продолжая уменьшать напряжение, можно увидеть, что лишь при некотором напряжении – напряжении гашения U_г, которое меньше, чем U_з, лампа “гаснет” и ток скачком резко падает. На этом самостоятельный разряд в лампе прекращается.

Для реальной лампы зависимость I=f(U) не является линейной, причем при U>U_з кривые, снятые при возрастании и убывании напряжения, не вполне совпадают.

Генератор состоит из источника , конденсатора емкостью С, сопротивления R и собственно газонаполненной лампы Л (рис.7.1). Такой генератор даёт колебания периодические, но негармонические. При подключении генератора к источнику  начальное сопротивление незажженной лампы велико, конденсатор С заряжается, одновременно растет напряжение на электродах лампы, подсоединенной параллельно конденсатору.

Когда разность потенциалов на электродах лампы достигнет значения напряжения зажиганияU_З, лампа “зажжется” – её сопротивление R_Л скачком уменьшится, и она начнет проводить ток. Так как R>>R_Л, то ток разряда конденсатора потечет через лампу. Это вызовет быстрое падение напряжения на конденсаторе, и когда оно достигнет значения напряжения гашения U_г, лампа “гаснет”, и процесс зарядки-разрядки начинается сначала. Возникают релаксационные колебания.

Кривая изменения напряжения на конденсаторе представлена на рис. 7.3 и представляет собой негармонические релаксационные колебания. В течение времени t₁ (передний фронт импульса) конденсатор заряжается; это – время накопления энергии. Когда напряжение на конденсаторе и лампе достигнет напряжения зажигания, конденсатор разряжается через горящую лампу в течение времени t₂ (задний фронт импульса); это – время сброса энергии. Период колебаний равен .

Найдем законы, по которым будет меняться напряжение на конденсаторе.

1) Рассмотрим процесс зарядки конденсатора С до напряжения U_з через сопротивление R (рис.7.1). Запишем второе правило Кирхгофа для замкнутого контура abcda

; (7.1)

где – разность потенциалов на обкладках конденсатора.

Сила тока по определению:

; (7.2)

Тогда

, или . (7.3)

Получено дифференциальное уравнение для заряда на конденсаторе. Подробное решение подобного уравнения описано в лабораторной работе 2-06 (см. формулу (6.5)). Результат:

. (7.4)

Покажем, что приведённая функция действительно является решением уравнения (7.3) путём подстановки (7.4) в (7.3), предварительно рассчитав производную:

;.

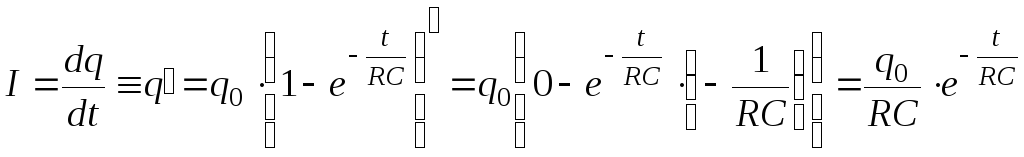Далее после сокращения:

;

или

.

Таким образом, найдено выражение для константы . Используя (7.4), найдём зависимость напряжения на конденсаторе от времени:

;

. (7.5)

Максимальное напряжение, до которого принципиально можно было бы зарядить конденсатор, равно ЭДС источника: (см. пунктир на рис.7.3). Однако при начинается процесс разрядки конденсатора через загоревшуюся лампу, и максимальная энергия, которую может запасти конденсатор, равна

.

2) Процесс разрядки конденсатора через лампу описывается дифференциальным уравнением (7.6), аналогичным уравнению (7.3), полученным также из второго правила Кирхгофа для контура dcefd:

; . (7.6)

Поскольку , то , и для напряжения

. (7.7)

Решением этого уравнения является функция (7.8):

, (7.8)

где что тоже доказывается подстановкой:

;

.

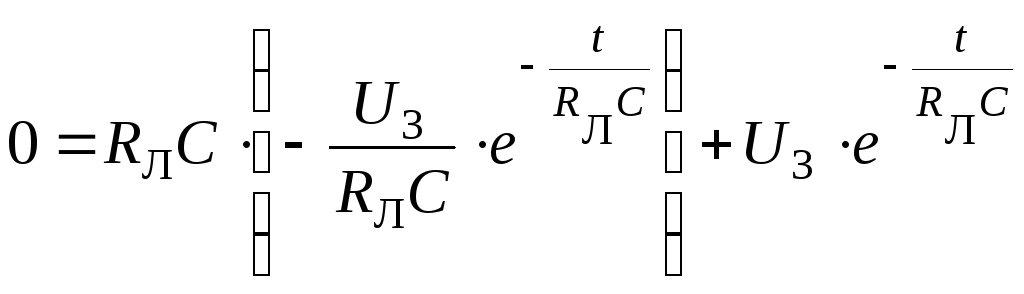
После сокращения

0=0.

На рис.7.4 приведён график функции (7.8); см. также рис.7.2.

Замечание. Оба процесса – зарядка и разрядка конденсатора – описываются экспоненциальными функциями (7.4) и (7.8), в показателях которых присутствует произведение . Произведение RС имеет размерность времени и называется постоянной времени, или временем релаксации :

. (6.11)

За время заряд конденсатора (или напряжение) уменьшается в e раз (e≈2.7 – основание натурального логарифма), то есть, постоянная времени характеризует быстроту соответствующего процесса. Поскольку разрядка происходит через лампу, сопротивление которой в режиме горения очень мало (R_Л<<R), тогда , и разрядка происходит существенно быстрее, чем зарядка.